Was sind periodische Vorgänge?

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Was sind periodische Vorgänge?
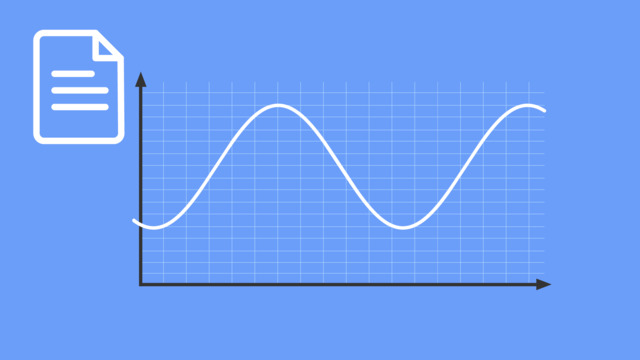
Mit Hilfe der Bewegung des Ventils von Karstens Hinterrad am Fahrrad erfährst du: Periodische Vorgänge wiederholen sich immer gleich und in gleichen zeitlichen oder räumlichen Abständen. Periodische Vorgänge können graphisch dargestellt werden. Der zu einem x-Wert gehörende y-Wert heißt Ausschlag. Der Kehrwert der Periodenlänge heißt Frequenz.
Transkript Was sind periodische Vorgänge?
Hallo und herzlich willkommen zum Thema: Was sind periodische Vorgänge? Wir wollen dir heute anhand eines Beispiels zeigen, was periodische Vorgänge sind. Im Alltag, in Natur und Technik gibt es Vorgänge, die sich regelmäßig und immer genau gleich wiederholen. Solche Vorgänge nennen wir periodisch. Karsten ist ein begeisterter Radfahrer. Sein Lehrer hat ihm folgende Aufgabe gestellt: Zeichne auf, wie sich die Höhe des Ventils über der Straße am Hinterrad deines Fahrrades verändert. Und zwar in Abhängigkeit von dem zurückgelegten Weg. Du wirst sehen, das ist ein periodischer Vorgang. Wie hat Karsten nun die Aufgabe gelöst? Karsten spielt die Bewegung des Rades durch das Abrollen einer CD auf einem Lineal nach. Er hat auf eine CD zwei Kreise aus Pappe geklebt. Der Punkt A ist die Radnabe. Der Punkt B stellt das Ventil dar. Beide sind durchstochen, damit er die Spitze eines Stifts hindurch bekommt. Damit lassen sich Punkte beim Abrollen der CD markieren. Karsten rollt das Radmodell langsam am Lineal entlang. Er stoppt und markiert das Ventil und die Radnabe. Karstens Bild sieht so aus. Die farbigen Punkte beschreiben die Bewegung des Ventils, die Schwarzen die der Nabe. Er verbindet die Punkte miteinander. Das Ventil beschreibt einen periodischen Vorgang. Die Nabe läuft geradeaus. Das ist sein Ergebnis. Am Diagramm sehen wir, dass die Bewegung sich wiederholt. Die Periodenlänge T gibt die kleinste Länge an, nach der sich der Vorgang wiederholt. Bei zeitlichen Vorgängen wird die Periodenlänge auch Periodendauer genannt. Ihr Wert ist immer größer null. Alle y-Werte wiederholen sich innerhalb einer Periode. Am Graphen kann man dies beispielhaft zeigen. Die beiden pinken Punkte begrenzen die Periode. In diesem Bereich vollzieht das Rad eine komplette Umdrehung. Die Frequenz f gibt an, wie viele Umläufe das Objekt pro Messeinheit x macht. Bei unserem Beispiel wäre die Messeinheit nun Meter. Die Messeinheit könnte bei anderen Aufgaben beispielsweise auch Sekunden sein. Die Frequenz ist damit immer der Kehrwert der Periodenlänge. Du hast heute an Karstens Experiment gelernt, was ein periodischer Vorgang ist. Viel Spaß auf der Suche nach weiteren periodischen Vorgängen im Alltag. Auf Wiedersehen.
Was sind periodische Vorgänge? Übung
-
Beschreibe periodische Vorgänge.
TippsEin nichtperiodischer Vorgang enthält kein erkennbares sich wiederholendes Muster oder wiederholt sich auf eine unregelmäßige Art und Weise.
Die Bewegung eines Flummis ist kein periodischer Vorgang, da die Sprunghöhe immer kleiner wird.
LösungIm Alltag, in Natur und Technik gibt es Vorgänge, die sich regelmäßig und immer genau gleich wiederholen. Diese nennen wir periodische Vorgänge.
Bei einem periodischen Vorgang kannst Du einen Teil des Vorgangs ausfindig machen, der sich genauso wiederholt. Zum Beispiel wiederholt das Ventil am Hinterrad eines Fahrrads immer wieder den Aufstieg und Abstieg von der tiefsten Position zur höchsten und wieder zurück auf die immer gleiche Weise.
Ein Gegenbeispiel: Die Bewegung eines Flummis ist kein periodischer Vorgang, denn die Sprunghöhe wird immer kleiner.
-
Bestimme die richtige Gleichung für die Frequenz $f$ in Abhängigkeit von der Periodenlänge $T$.
TippsDie Frequenz ist die Anzahl der Umläufe pro Messeinheit.
Das Produkt von Periodenlänge und Frequenz ist immer $1$.
LösungDie Frequenz eines periodischen Vorganges ist die Anzahl der Umläufe pro Messeinheit. Du kannst sie als Kehrwert der Periodenlänge berechnen: $f=\frac{1}{T}$.
Diese Gleichung lässt sich noch in eine weitere Gleichung umwandeln. Wenn ich den Kehrwert auf beiden Seiten bilde, bleibt die Gleichung korrekt und ich erhalte $\frac{1}{f}=T$ bzw. $T=\frac{1}{f}$. Diese Gleichung ist also ebenfalls korrekt.
Eine gute Merkregel ist die folgende: Das Produkt von Periodenlänge und Frequenz ist immer $1$, d.h. es gilt $f\cdot T=1$. Diese Gleichung erhältst du, wenn du in der Ausgangsgleichung $f=\frac{1}{T}$ auf beiden Seiten mit $T$ multiplizierst.
-
Berechne die gesuchten Frequenzen.
TippsBei Frequenzen steht die Enheit unter dem Bruchstrich.
Du musst die Einheiten in Minuten bzw. Dezimeter umrechnen.
Die Frequenz ist der Kehrwert der Periodendauer bzw. der Periodenlänge.
LösungWenn der Minutenzeiger wieder an der gleichen Stelle ist, ist genau eine Periode vorüber. Dafür benötigt er $1$ Stunde oder $60$ Minuten, also ist dies auch seine Periodendauer. Seine Frequenz ist der Kehrwert der Periodendauer, also $\frac{1}{60~min}$.
Wenn die Propellerspitze wieder an ihrer Ausgangsposition ist, hat sie eine Periode zurückgelegt und $6~m=60~dm$ hinter sich gebracht. Die Periodenlänge ist dann $60~dm$. Die Frequenz der Kehrwert der Periodenlänge, hier $\frac{1}{60~dm}$.
-
Entscheide, welche Gleichungen korrekt sind.
TippsDie Frequenz ist die Anzahl der Umläufe pro Messeinheit.
Die Frequenz ist der Kehrwert der Periodenlänge; d.h. es gilt: $f=\frac{1}{T}$.
LösungDie Frequenz ist per Definition immer der Kehrwert der Periodenlänge: $f=\frac{1}{T}$.
- Wenn du nun auf beiden Seiten den Kehrwert bildest, erhältst du $T=\frac{1}{f}$.
- $f\cdot T$ lässt sich dann auch schreiben als $\frac{f}{f}$, da $T=\frac{1}{f}$ ist und es ergibt sich $f\cdot T=\frac{f}{f}=1$.
- Ebenso lässt sich $\frac{f}{T}$ umschreiben, z. B. als $\frac{f}{\frac{1}{f}}$. Dies lässt sich als Multiplikation mit dem Kehrwert des Nenners schreiben: $f\cdot f=f^2$. Daher gilt, dass $\frac{f}{T}=f^2$ ist.
- $2\cdot T$ ist wegen der Beziehung der Periodendauer und der Frequenz zueinander nichts anderes als $2\cdot\frac{1}{f}=\frac{2}{f}$.
-
Definiere die Begriffe Periodenlänge und Frequenz.
TippsDie Frequenz ist der Kehrwert der Periodenlänge.
LösungDie Periodenlänge ist die kleinste Länge nach der sich ein Vorgang wiederholt. Die Periode geht also vom Start des Vorgangs bis zum ersten Punkt, bei dem sich der Vorgang wiederholt.
Die Frequenz ist definiert als die Anzahl der Umläufe für eine bestimmte Messeinheit x. Sie gibt also an, wie oft sich der Vorgang innerhalb der Messeinheit x wiederholt. Die Messeinheit kann dabei unterschiedlich ausfallen. Die Frequenz ist der Kehrwert der Periodenlänge. Ist also die Periodenlänge $1~m$, so ergibt die Frequenz $\frac{1}{m}$.
-
Ordne den Größen die korrekten Werte mit ihren Einheiten zu.
Tipps$1~Hz$ entspricht gerade $1\cdot s^{-1}$.
Beachte: Bei Frequenzen stehen die Zeit- und Längeneinheiten jeweils im Nenner.
LösungWir ordnen die Werte zu:
- $11~\frac{1}{min}$, $\frac{1}{km}$, $\frac{7}{cm}$ und $\frac{8}{10m}$ sind der Frequenz $f$ zuzuordnen, da die Messeinheit in jedem Fall im Nenner auftaucht und die Frequenz definiert ist als „Anzahl der Umläufe pro Messeinheit $x$“.
- $20~Hz$ ist ebenfalls der Frequenz zuzuordnen, da es sich bei $Hz$ um eine zusammengesetzte Einheit handelt und $1~Hz=1~\frac{1}{s}$ entspricht.
- Entsprechend sind $5~s$ und $78~m$ der Periodenlänge $T$ zuzuordnen. $69~\frac{1}{kHz}$ wiederum gehört auch zur Periodenlänge $T$, denn $\frac{1}{kHz}=\frac{1}{\frac{1000}{s}}=\frac{1}{1000} s$, weil $Hz$ eine zusammengesetzte Einheit darstellt.
9'182
sofaheld-Level
6'600
vorgefertigte
Vokabeln
7'643
Lernvideos
35'607
Übungen
32'360
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?