Periodische Vorgänge beschreiben und modellieren

Inhaltsverzeichnis zum Thema

• Was sind periodische Vorgänge?
• Beispiele
• Periodenlänge und Frequenz
• Die Sinusfunktion
• Modellierung von periodischen Vorgängen

Was sind periodische Vorgänge?

Es gibt Vorgänge, die sich im gleichen Zeitraum oder in gleichen Abständen immer genau gleich wiederholen. Solche Vorgänge nennt man periodische Vorgänge.

Beispiele

• Ein Kühlschrank ist auf eine bestimmte Temperatur eingestellt. Der ungeöffnete Kühlschrank erwärmt sich bis zu einer gewissen Temperatur und wird dann wieder auf die Ausgangstemperatur herabgekühlt. Dieser Vorgang wiederholt sich in bestimmten Abständen. Bei etwas älteren Modellen kann man dieses Abkühlen auch hören.
• Die Atmung eines Menschen ist periodisch.
• Jeder Wochentag wiederholt sich alle sieben Tage. Auch dies ist ein periodischer Vorgang.
• Du hast jedes Jahr am gleichen Tag Geburtstag.

Die kleinste Länge (der kleinste Zeitraum) nach dem sich ein Vorgang wiederholt, wird als Periodenlänge (Periodendauer) $T$ bezeichnet.

Die Frequenz $f$ eines periodischen Vorganges gibt, an wie oft sich der periodische Vorgang in einem gegebenen Zeitraum $Z$ wiederholt. Sie lässt sich wie folgt berechnen.

$\quad f=\frac1T\cdot Z$

Mit diesen Größen lassen sich periodische Vorgänge beschreiben.

Periodenlänge und Frequenz

Schau dir nochmal die obigen Beispiele an:

• Die Periode des Abkühlens bei einem Kühlschrank hängt sicher von den entsprechenden Temperaturen ab. Sei die Periode zum Beispiel $10~min$, dann kann damit die Frequenz berechnet werden. Die Frequenz gibt an, wie häufig sich der periodische Vorgang in einem gegebenen Zeitraum wiederholt. Willst du wissen, wie oft sich der Aufwärm- und Abkühlvorgang beim Kühlschrank in einer Stunde, also $60~min$ wiederholt, rechnest du

$\quad ~~ f=60~min~\cdot ~\frac 1{10~min}= 6 $ .

• Die Periode bei der menschlichen Atmung beträgt ungefähr $3~s$. Damit kann die Häufigkeit der Atmung pro Minute berechnet werden. Diese Zahlen variieren natürlich.

$\quad ~~ f= 60~s~\cdot\frac 1{3~s}= 20 $.

• Die Periode von Wochentagen ist $T=7$ Tage. Alle $7$ Tage wiederholt sich der Vorgang genau einmal.
• Dein Geburtstag wiederholt sich jedes Jahr. Also ist die Periode $1$ Jahr.

Die Sinusfunktion

Die Sinusfunktion $f(x)=\sin(x)$ ist ein Beispiel für eine periodische Funktion.

Eine Funktion $f(x)$ ist eine periodische Funktion, wenn mindestens eine Zahl $p$ existiert, dass für alle $x$ gilt $f(x+p)=f(x)$. Die kleinste Zahl, die dies erfüllt, ist die Periodenlänge.

Hier siehst du den Graphen der Sinusfunktion.

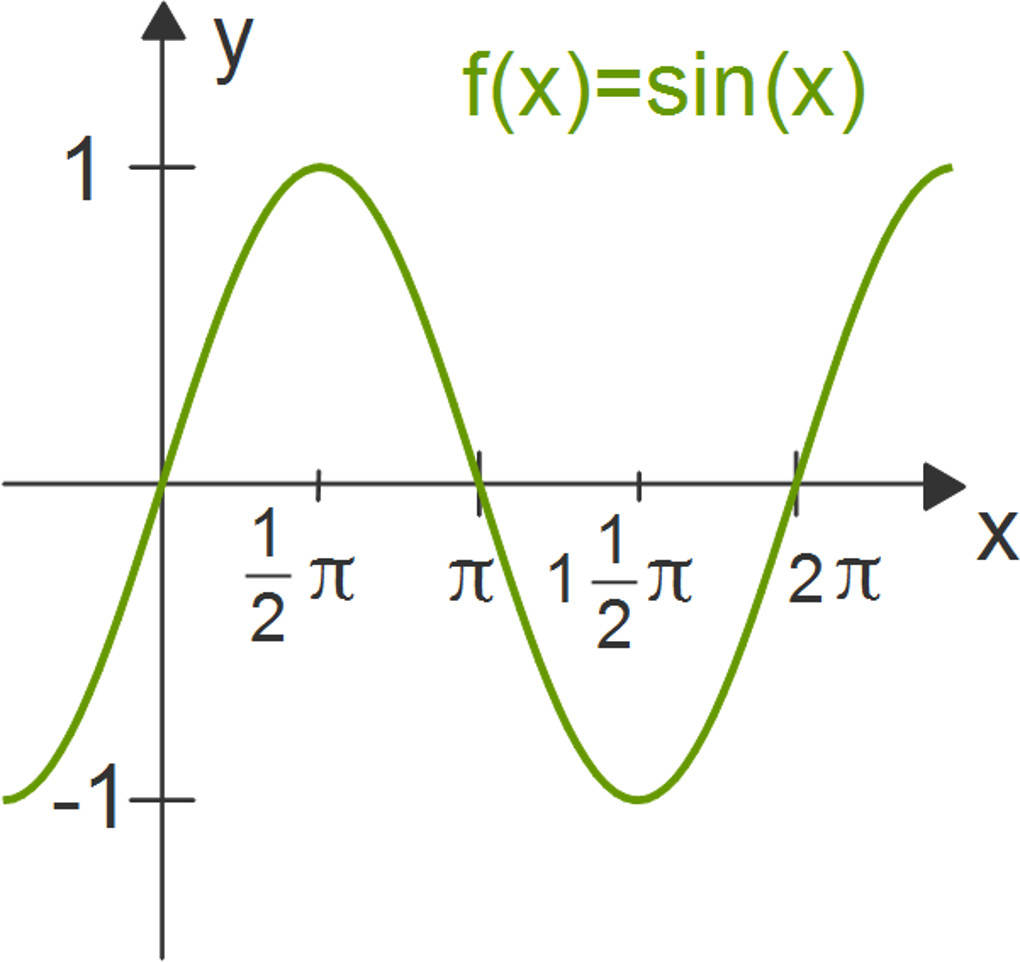
Erkennst du die Periodenlänge? Richtig: Diese ist $2~\pi$.

$\pi=3,1415...$ ist die sogenannte Kreiszahl.

Modellierung von periodischen Vorgängen

Mit Hilfe der Sinusfunktion können periodische Vorgänge modelliert werden:

$f(x)=a\cdot \sin(bx-d)+e$.

Hierfür benötigst du

• den maximalen Wert,
• den minimalen Wert sowie
• das arithmetische Mittel dieser beiden Werte.

Wie können nun die einzelnen Parameter bestimmt werden?

Dafür betrachten wir als Beispiel die menschliche Atmung.

Ein Mensch atmet pro Minute 20 mal ein und aus. Dadurch ändert sich das Lungenvolumen. Am Ende einer Einatmung befinden sich ungefähr $6,5~L$ Luft in der Lunge, am Ende einer Ausatmung $1,2~L$. Das Befüllen und Entleeren der Lunge kann als periodischer Prozess modelliert werden.

• Der maximale Wert ist $6,5~L$,
• der minimale $1,2~L$.
• Das arithmetische Mittel beträgt

$\quad~~ \frac{6,5+1,2}2=3,85~L$

Die Periode ist gegeben durch $T=\frac{60~s}{20}=3~s$ und die Frequenz (pro Minute) ist die angegebene Zahl der Atemzüge $20$.

• Der Parameter $a$ steht für die Amplitude. Dies ist die maximale Abweichung der Werte von dem arithmetischen Mittel. Hier ist

$\quad~~ a=\frac{6,5-1,2}2=2,65$.

• Der Paramater $b$ berechnet sich wie folgt

$\quad~~ b=\frac{2~\pi}T=\frac{2~\pi}3\approx 2,09$ .

• Der Parameter $d$ ist der Wert, an dem erstmals das arithmetische Mittel angenommen wird, bevor ein maximaler Wert erreicht wird. Wenn man zum Beispiel $x=0$ als Beginn einer Einatmung betrachtet, dann ist $d=0$.
• Der Parameter $e$ ist das arithmetische Mittel, also $e=3,85$.

Gesamt ist die menschliche Atmung somit modelliert durch

$f(x)=2,65\cdot \sin(2,09x)+3,85$.

Der zugehörige Verlauf ist hier zu sehen.

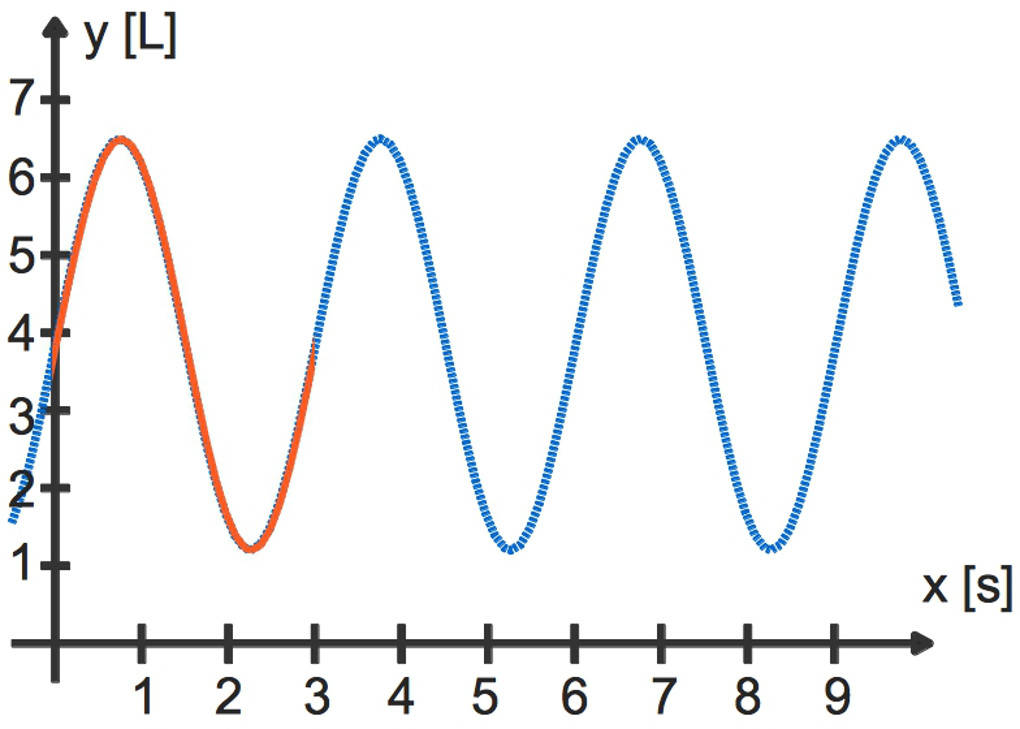
In rot hervorgehoben ist der Verlauf der periodischen Funkion auf einer Periodenlänge $[0;3]$.