Strecken in Verhältnisse teilen – innere Teilung
Messskalen auf einem Messbecher helfen dabei, Mengen gleichmäßig aufzuteilen. Um eine Strecke im gewünschten Verhältnis zu teilen, kann man einen Hilfsstrahl und einen Zirkel verwenden. Lerne, wie du das in der Praxis umsetzen kannst! Interessiert? Weitere Informationen und Übungen erwarten dich im Text.

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Strecken in Verhältnisse teilen – innere Teilung
Strecken in Verhältnisse teilen – Anwendungsbereich Messskala
Auf einem Messbecher ist meistens eine Skala dargestellt. Diese besteht aus Strichen, die alle den gleichen Abstand voneinander haben. Die Höhe des Messbechers wird damit in gleich große Abschnitte geteilt. Dadurch können wir Mengen, beispielsweise von Zutaten, in einem bestimmten Verhältnis abmessen. Wir können die Messskala auch selbst erstellen – wenn wir aus der Geometrie eine Strecke mit der inneren Teilung im Verhältnis teilen können.
Strecken in Verhältnisse teilen – Beispiel
Wir wollen an einem Beispiel der Frage Wie teilt man eine Strecke im Verhältnis mit der inneren Teilung? nachgehen. Die Strecke $AB$ soll im Verhältnis $3:2$ geteilt werden.
Wir konstruieren dieses Verhältnis, indem wir die Strecke in $5$ gleich große Teile unterteilen. Dazu zeichnen wir einen Hilfsstrahl durch den Punkt $A$. Der Hilfsstrahl bildet mit der Strecke $AB$ einen spitzen Winkel. Dann stechen wir den Zirkel im Punkt $A$ ein und zeichnen einen Kreisbogen mit beliebigem Radius, der den Hilfsstrahl schneidet. Am Schnittpunkt stechen wir den Zirkel wieder ein und zeichnen mit dem gleichen Radius wieder einen Kreisbogen. Das wiederholen wir, bis wir $5$ Stücke abgetragen haben.
Mit dem Geodreieck verbinden wir dann den letzten Schnittpunkt auf dem Hilfsstrahl mit dem Punkt $B$ auf der Strecke $AB$. Mit einem zweiten Geodreieck führen wir dann eine Parallelverschiebung dieser Verbindungslinie durch und zeichnen eine Parallele durch jeden Schnittpunkt auf dem Hilfsstrahl.
Damit ist die Strecke $AB$ in fünf gleich große Stücke unterteilt. Diese müssen wir noch abzählen, um das gesuchte Verhältnis $3;2$ zu finden.
Strecken in Verhältnisse teilen – allgemeines Vorgehen
Zur inneren Teilung einer Strecke $AB$ im Verhältnis $a:b$ gehen wir wie folgt vor:
- Einen Hilfsstrahl durch den Punkt $A$ zeichnen
- Mit dem Zirkel $a+b$ viele gleich große Strecken abtragen
- Den letzten Schnittpunkt mit dem Punkt $B$ verbinden
- Mit Parallelverschiebung alle anderen Schnittpunkte mit der Strecke $AB$ verbinden
- Vom Punkt $A$ aus $a$ viele Teilstrecken abzählen
Strecken in Verhältnisse teilen – weitere Übungen
Jetzt kannst du eine Strecke mit Zirkel und Lineal teilen. Wir haben zunächst an einem Beispiel das Teilen einer Strecke im Verhältnis 3:2 per innerer Teilung einfach erklärt. Wenn du üben möchtest, Strecken mit der inneren Teilung in Verhältnisse zu teilen, wirst du hier bei sofatutor fündig. Hier gibt es auch noch ein Arbeitsblatt zum Thema Strecke im Verhältnis teilen.
Transkript Strecken in Verhältnisse teilen – innere Teilung
Walter wills wieder wissen. In seinem - verhältnismäßig aufgeräumten - Labor arbeitet er an seiner neuesten Kreation. Hoffentlich hat er die Füllhöhen in seinem Reagenzglas richtig berechnet. Nur noch ein letzter Tropfen. Nein, hat er anscheinend nicht. Damit es beim nächsten Mal besser klappt, muss Walter Strecken in Verhältnisse teilen - per innerer Teilung. Was hat Walter falsch gemacht? Hier ist sein Reagenzglas. Das hat ja gar keine Füllhöhenmarkierungen! Da wollte Walter wohl wieder am falschen Ende sparen. Die Höhe des Reagenzglases zeichnen wir als Strecke AB ein. Walter will die Zutaten im Verhältnis 3 zu 2 mischen. Also müssen wir die Strecke AB im Verhältnis 3 zu 2 teilen. Wir konstruieren dieses Verhältnis, indem wir mit Zirkel und Geodreiecken die Strecke in gleich große Stücke unterteilen. Um das Verhältnis 3 zu 2 zu konstruieren, teilen wir die Strecke AB in 3 plus 2, also 5 gleich große Teile auf. Wie ging das nochmal? Wir zeichnen einen Hilfsstrahl durch den Punkt A. Der kann so lang sein, wie du es brauchst. Er sollte nur in einem spitzen Winkel zur Strecke AB stehen. Dann stichst du den Zirkel im Punkt A ein und stellst ihn auf einen beliebigen Radius ein. Der sollte nicht zu klein sein, aber auch nicht so groß. Mit dem Zirkel zeichnest du einen Kreisbogen, der den Hilfsstrahl schneidet. Am Schnittpunkt stichst du den Zirkel wieder ein und lässt den Radius gleich. Dann zeichnest du wieder einen Kreisbogen. Das wiederholst du, bis du die gewünschten 5 Stücke abgetragen hast. Mit dem Geodreieck verbindest du den letzten Schnittpunkt auf dem Hilfsstrahl mit dem Punkt B auf der Strecke AB. Mit einem zweiten Geodreieck kannst du nun eine Parallelverschiebung dieser Verbindungslinie durchführen. Und zwar zeichnest du eine Parallele durch jeden Schnittpunkt auf dem Hilfsstrahl. Damit hast du die Strecke AB in 5 gleich große Stücke unterteilt. Die musst du jetzt nur noch abzählen, um das gesuchte Verhältnis 3 zu 2 zu finden. Dieses Höhenverhältnis muss Walter jetzt noch auf sein Reagenzglas übertragen. Okay, also hätte Walter sein Reagenzglas so befüllen müssen. Aber er hat es aus Versehen im Verhältnis 2 zu 3 gefüllt! Darauf muss man besser acht geben! Während Walter werkelt und seine Mischung neu ansetzt, fassen wir nochmal zusammen. Um eine Strecke AB in einem vorgegebenen Verhältnis a zu b zu teilen, gehst du so vor: Zunächst zeichnest du einen Hilfsstrahl durch den Punkt A. Denk daran, dass der Hilfsstrahl lang genug wird und der Winkel spitz sein sollte. Dann trägst du mit dem Zirkel a plus b viele gleich große Strecken ab, bei Walter waren das 3 plus 2, also 5. Den letzten Schnittpunkt verbindest du mit dem Punkt B. Per Parallelverschiebung verbindest du alle anderen Schnittpunkte auf dem Hilfsstrahl mit der Strecke AB. Zum Schluss musst du nur noch abzählen: nämlich a viele Teilstrecken vom Punkt A aus. Dann bist du fertig: die übrigen Teilstrecken sind genau b viele. Walters wahnwitziges Werk ist vollbracht. Was hat er da eigentlich gebraut? Achse, eine scharfe Sauce für seine Currywürste. Die schmecken bestimmt verhältnismäßig lecker!
Strecken in Verhältnisse teilen – innere Teilung Übung
-
Gib an, wie du eine Strecke $\overline{AB}$ in einem Verhältnis von $a:b$ per innerer Teilung zerlegen kannst.
TippsHier abgebildet ist der vierte Schritt beim Teilen einer Strecke $\overline{AB}$ in ein Verhältnis von $3:2$.
Im letzten Schritt liegen auf der Strecke $\overline{AB}$ genau $a+b$ viele gleich große Teilstrecken vor. Diese müssen nach dem vorgegebenen Verhältnis abgezählt werden.
LösungMöchtest du eine Strecke $\overline{AB}$ in einem Verhältnis von $a:b$ teilen, so gehst du wie folgt vor:
- Zunächst zeichnest du einen Hilfsstrahl durch den Punkt $A$. Denk daran, dass der Hilfsstrahl lang genug ist und der Winkel im Punkt $A$ spitz sein sollte.
- Danach trägst du auf dem Hilfsstrahl mit einem Zirkel $a+b$ viele gleich große Strecken ab.
- Den letzten Schnittpunkt auf dem Hilfsstrahl verbindest du dann mit dem Punkt $B$ der Strecke $\overline{AB}$.
- Per Parallelverschiebung verbindest du als Nächstes alle anderen Schnittpunkte auf dem Hilfsstrahl mit der Strecke $\overline{AB}$.
- Zum Schluss musst du $a$ viele Teilstrecken ausgehend vom Punkt $A$ abzählen. Es bleiben dann genau $b$ viele Teilstrecken übrig.
-
Beschreibe, wie du die Strecke $\overline{AB}$ in das Verhältnis $3:2$ teilst.
TippsTeilt man eine Strecke $\overline{AB}$ in ein Verhältnis $a:b$, dann muss die Strecke in $a+b$ gleich große Abschnitte aufgeteilt werden.
Genau so viele Strecken benötigt man auf dem Hilfsstrahl.
Ist eine Strecke $\overline{AB}$ in $a+b$ gleich große Teilstrecken geteilt, so liegt der Teilungspunkt für das Verhältnis $a:b$ hinter $a$ Teilstrecken.
LösungWir möchten in dieser Aufgabe eine Strecke $\overline{AB}$ im Verhältnis $3:2$ teilen. Hierzu gehen wir wie folgt vor:
- Wir zeichnen uns einen Hilfsstrahl durch den Punkt $A$ mit einem spitzen Winkel in $A$.
- Dann tragen wir mit einem Zirkel drei plus zwei, also fünf, gleich große Strecken auf dem Hilfsstrahl ab.
- Anschließend verbinden wir mit einem Geodreieck den letzten Schnittpunkt auf dem Hilfsstrahl mit dem Punkt $B$ der Strecke $\overline{AB}$.
- Nun führen wir mithilfe eines weiteren Geodreiecks eine Parallelverschiebung dieser Verbindung durch alle anderen Schnittpunkte durch.
- Dadurch entstehen auf der Strecke $\overline{AB}$ fünf gleich große Teilstrecken. Ausgehend vom Punkt $A$ müssen wir jetzt drei Teilstrecken abzählen. Dann bleiben genau zwei weitere Teilstrecken übrig.
-
Ermittle die Lage der gegebenen Teilungspunkte.
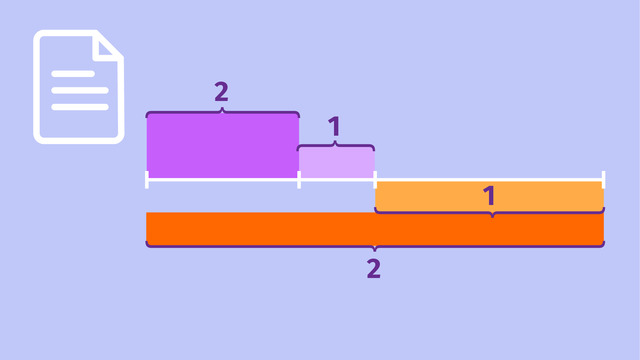
TippsAuf der Strecke $\overline{AB}$ gibt es $20$ gleich große Teilstrecken, wenn jede Teilstrecke die Länge $1$ hat.
Wenn jede Teilstrecke die Länge $2$ hat, erhältst du $10$ gleich große Teilstrecken.
Wenn du die Strecke $\overline{AB}$ in einem Verhältnis von $a:b$ teilst, dann bildest du $a+b$ gleich große Teilstrecken auf $\overline{AB}$. Anschließend zählst du vom Punkt $A$ ausgehend $a$ viele Teilstrecken ab. Genau an dieser Stelle liegt der gesuchte Teilungspunkt.
LösungLass uns diese Aufgabe gemeinsam anschauen: Gegeben ist eine Zahlengerade, auf der zwei Positionen markiert sind: der Punkt $A$ bei $-2$ und der Punkt $B$ bei $18$.
Es sind zudem die Teilungsverhältnisse dreier Teilungspunkte der Strecke $\overline{AB}$ gegeben. Diese lauten:
- $T_1$ bei $2:3$
- $T_2$ bei $1:3$
- $T_3$ bei $6:4$
- Wir bestimmen, in wie viele Teilstrecken die Strecke $\overline{AB}$ geteilt werden muss. Für ein Verhältnis $a:b$ wird die Strecke in $a+b$ gleich große Teilstrecken geteilt.
- Dann schauen wir, wie viele Teilstrecken wir ausgehend vom Punkt $A$ „gehen“ müssen, um an den Teilungspunkt zu gelangen.
Teilungspunkt $T_1$
Gegeben ist das Verhältnis $2:3$. Wir teilen die Strecke $\overline{AB}$ in $2+3$, also $5$, gleich große Teilstrecken. Wir teilen anschließend $20$ durch $5$ und erhalten eine Schrittweite von $4$. Wir müssen die Zahlengerade demnach in Viererschritte teilen. Nun gehen wir von Punkt $A$ aus $2$ Viererschritte und landen somit bei $-2+2\cdot 4=6$. Unser Teilungspunkt $T_1$ liegt also bei der $6$.
Teilungspunkt $T_2$
Das Vorgehen ist analog zu $T_1$. Gegeben ist das Verhältnis $1:3$, also $1+3=4$ gleich große Teilstrecken. Wir teilen jetzt $20$ durch $4$ und erhalten eine Schrittweite von $5$. Wir gehen demnach von Punkt $A$ aus einen Fünferschritt und landen somit bei $-2+1\cdot 5=3$. Unser Teilungspunkt $T_2$ liegt also bei der $3$.
Teilungspunkt $T_3$
Gegeben ist das Verhältnis $6:4$, also $10$ gleich große Teilstrecken. Wir haben demnach eine Schrittweite von $\frac{20}{10}=2$. Wir gehen von Punkt $A$ aus $6$ Zweierschritte und landen somit bei $-2+6\cdot 2=10$. Unser Teilungspunkt $T_3$ liegt also bei der $10$.
-
Bestimme die gesuchte Entfernung.
TippsDu kannst diese Aufgabe auch zeichnerisch lösen. Nimm hierzu an, dass ein Zentimeter auf deiner Zeichnung einem Kilometer entspricht. Zeichne dann eine Strecke $\overline{AB}$ der Länge $12\ \text{cm}$ und teile diese in einem Verhältnis von $2:4$. Miss anschließend die Länge der Strecke von $A$ bis zum Teilungspunkt $T$.
Auch rechnerisch lässt sich die Aufgabe gut lösen. Dafür teilst du die Strecke von $12\ \text{km}$ in gleich große Teilstrecken. Die Anzahl dieser Teilstrecken erhältst du aus dem Verhältnis $2:4$.
Es handelt sich um $2+4 = 6$ gleich große Teilstrecken.
LösungLass uns diese Aufgabe gemeinsam zuerst rechnerisch lösen:
Wir teilen die Strecke von $12$ Kilometer Länge in $2+4=6$ gleich große Teilstrecken. So erhalten wir $6$ Teilstrecken mit einer Länge von je $\frac{12}6=2$ Kilometern. Nun gehen wir von Punkt $A$ aus $2\cdot 2=4$ Kilometer bis zu dem Zuhause von Tatjana $T$. Damit hat die Strecke $\overline{AT}$ eine Länge von $4$ Kilometern.
Diese Aufgabe kannst du auch zeichnerisch lösen. Hierzu gehst du wie folgt vor:
- Nimm zunächst an, dass ein Zentimeter auf deiner Zeichnung einem Kilometer entspricht.
- Zeichne dann die Strecke $\overline{AB}$ mit einer Länge von $12\ \text{cm}$.
- Zeichne einen Hilfsstrahl durch den Punkt $A$.
- Trage mit einem Zirkel $2+4=6$ gleich große Strecken auf dem Hilfsstrahl ab.
- Verbinde den letzten Schnittpunkt mit $B$.
- Führe eine Parallelverschiebung dieser Verbindung durch alle anderen Schnittpunkte durch.
- Zähle das Verhältnis $2:4$ auf der Strecke $\overline{AB}$ ab und markiere den Punkt $T$.
- Miss die Strecke $\overline{AT}$ ab und beachte den gewählten Maßstab.
-
Gib an, in welchem Verhältnis der jeweilige Teilungspunkt die Strecke $\overline{AB}$ teilt.
TippsHier abgebildet ist die Strecke $\overline{AB}$, welche in einem Verhältnis von $3:2$ geteilt wurde.
Wenn eine Strecke $\overline{AB}$ in einem Verhältnis von $a:b$ per innerer Teilung geteilt ist, dann gilt:
Um den Teilungspunkt zu finden, musst du von $A$ ausgehend $a$ Teilstrecken abzählen.
LösungEs ist die Strecke $\overline{AB}$ gegeben, die in fünf gleich große Teilstrecken geteilt ist. Zudem sind drei Teilungspunkte $T_1$, $T_2$ und $T_3$ gegeben. Gesucht sind die zugehörigen Teilungsverhältnisse.
Es gilt:
Ist eine Strecke $\overline{AB}$ in einem Verhältnis von $a:b$ per innerer Teilung geteilt, so liegt der Teilungspunkt $T$ ausgehend von dem Punkt $A$ hinter $a$ Teilstrecken.
Also betrachten wir, hinter der wievielten Teilstrecke der gegebene Teilungspunkt liegt. Dieser Wert entspricht dem ersten Wert unseres Verhältnisses. Da wir insgesamt fünf Teilstrecken haben, erhalten wir den zweiten Wert aus der Differenz.
Teilungspunkt $T_1$
Vor diesem Punkt befindet sich nur eine Teilstrecke. Somit ist unser erster Wert die $1$. Den zweiten erhalten wir aus $5-1$, also $4$. $T_1$ teilt die Strecke $\overline{AB}$ also in einem Verhältnis von $1:4$.
Teilungspunkt $T_2$
Wir gehen hier genauso vor wie für $T_1$. Dadurch ergibt sich, dass der Teilungspunkt $T_2$ die Strecke $\overline{AB}$ in einem Verhältnis von $2:3$ teilt.
Teilungspunkt $T_3$
Der Teilungspunkt $T_3$ teilt die Strecke $\overline{AB}$ in einem Verhältnis von $4:1$.
-
Prüfe die Aussagen zu einer beliebigen Strecke $\overline{AB}$ auf ihre Richtigkeit.
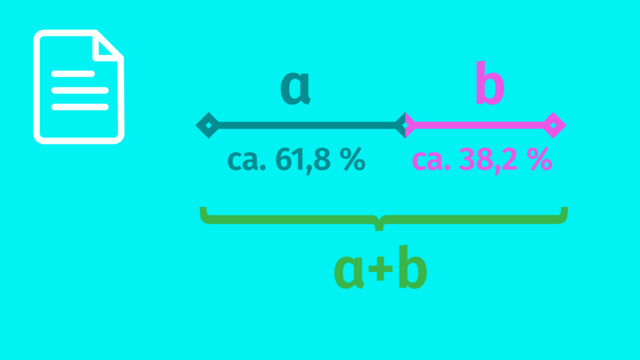
TippsEin Drittel der roten Strecke entspricht der Hälfte der gelben Strecke.
Teilt ein Teilungspunkt $T$ eine Strecke $\overline{AB}$ im Verhältnis $1:1$ per innerer Teilung, so erhält man zwei gleich lange Strecken $\overline{AT}$ und $\overline{TB}$.
Dieselben Strecken ergeben sich bei einem Verhältnis von $20:20$ bzw. $30:30$.
LösungIn dieser Aufgabe solltest du Aussagen zu einer beliebigen Strecke $\overline{AB}$ prüfen.
Es gilt allgemein:
Teilt ein Teilungspunkt $T$ die Strecke $\overline{AB}$ in einem Verhältnis von $a:b$ per innerer Teilung, ist $\frac 1a\cdot\overline{AT}$ genauso lang wie $\frac 1b\cdot\overline{BT}$.
Wenn wir nun ein Verhältnis von $9:1$ betrachten, so gilt laut der obigen Tatsache:
$ \begin{array}{lllll} \frac 19\cdot\overline{AT} &=& \frac 11\cdot\overline{TB} && \vert\cdot 9 \\ \overline{AT} &=& 9\cdot\overline{TB} \end{array} $
Es ist also wahr, dass die Strecke $\overline{AT}$ die neunfache Länge der Strecke $\overline{BT}$ hat, wenn der Teilungspunkt $T$ die Strecke $\overline{AB}$ in einem Verhältnis von $9:1$ per innerer Teilung teilt.
Zudem gilt dann:
Teilt der Teilungspunkt $T$ die Strecke $\overline{AB}$ in einem Verhältnis von $4:8$ per innerer Teilung, ist $\frac 14\cdot\overline{AT}$ genauso lang wie $\frac 18\cdot\overline{BT}$.
Des Weiteren liefert eine innere Teilung für das Verhältnis $50:50$ für jede Strecke eine Lösung. Diese entspricht der Lösung für die Verhältnisse $1:1$ sowie $2:2$ sowie $3:3$ usw. Es teilt die Strecke $\overline{AB}$ genau in der Mitte.
9'178
sofaheld-Level
6'600
vorgefertigte
Vokabeln
7'638
Lernvideos
35'608
Übungen
32'354
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?














Nice
ALLE deine Videos sind sooooo klasse, und super verständlich erklärt. Sie sind für mich meiner Meinung nach auch die besten Mathe Erklärungsvideos, die ich je hier auf sofatutor gesehen hab! :D
Seit Wann gibt es dieses Video
Seit wann kann eine Curry Soße explodieren 😱😱
das ist keinen Reagenzglaß.....das ist einen Messbecher.....aber sonst ist da ein sehr gutes video