Quadratischen Gleichungen – Anwendungsaufgaben

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Quadratischen Gleichungen – Anwendungsaufgaben
Hallo und herzlich willkommen. Heute wollen wir uns Textaufgaben zu quadratischen Gleichungen und Rechtecken anschauen. Textaufgaben zu quadratischen Gleichungen treten häufig bei der Berechnung des Flächeninhalts eines Rechtecks auf. Zunächst wiederholen wir gemeinsam, was man unter einer quadratischen Gleichung versteht. Im Anschluss lösen wir gemeinsam einige Textaufgaben zu quadratischen Gleichungen. Hierbei lernst du die Herangehensweise an solche Aufgabentypen. Viel Spaß.
Quadratischen Gleichungen – Anwendungsaufgaben Übung
-
Beschreibe, wie du die Seitenlänge $a$ einer $441~m^2$ großen quadratischen Fläche berechnest.
TippsDer Flächeninhalt eines Rechtecks wird mit $A = a \cdot b$ berechnet.
Eine Strecke verbindet zwei Punkte und ist somit stets größer $0$.
LösungGegeben ist eine quadratische Fläche mit dem Flächeninhalt von $A = 441~m^2$. Quadratische Flächen besitzen immer vier gleich lange Seiten, die rechte Winkel einschließen, sodass du die Fläche als $A = a \cdot a = a^2$ berechnen kannst.
Bei einer $441~m^2$ großen Fläche ergibt sich also die Gleichung $441 = a^2$, welche mit der Quadratwurzel zu lösen ist. Dafür ist es hilfreich, bis zu einem gewissen Bereich das Quadrat einer Zahl zu kennen, beispielsweise $19^2 = 361$, $20^2 = 400$ oder $21^2 = 441$. Auf diese Weise fällt dir die Lösung geradezu in den Schoß.
Es ist nur wichtig zu beachten, dass beim Verwenden der Quadratwurzel immer zwei Ergebnisse herauskommen, einmal ein positives und einmal ein negatives. In unserem Fall ist $\sqrt{441} = \pm 21$.
Da die Länge einer Strecke nicht negativ sein kann, fällt in diesem Fall das negative Ergebnis weg.
Die gesuchte Strecke $a$ beträgt $21~m$. Die Probe bestätigt uns, dass $a^2 = 21^2 = 441$ und $A = 441$ übereinstimmen.
-
Bestimme die Seitenlängen des $27~m^2$ großen Rechtecks, deren Seite $b$ dreimal so lang ist wie $a$.
TippsWenn eine Strecke $x$ doppelt so lang wie eine Strecke $y$ ist, lässt sich $x$ durch $2y$ beschreiben.
Vernachlässige das negative Ergebnis, nachdem du die Quadratwurzel gezogen hast.
LösungDie uns gegebene Fläche besitzt den Flächeninhalt $A = 27~m^2$. Im Allgemeinen berechnest du den Flächeninhalt eines Rechtecks mit $A = a \cdot b$.
In unserer Aufgabe ist uns keine Seite gegeben, aber wir wissen, dass die Seite $b$ dreimal so lang ist wie $a$. Das können wir mathematisch ausdrücken durch $b = 3a$. Jetzt können wir $b$ in $27 = a \cdot b$ einsetzen und haben plötzlich nur noch eine Variable.
$27 = a \cdot 3a$ lässt sich zu $27 = 3a^2$ vereinfachen. Nun ist es wichtig, dass du die Rechengesetze befolgst. Erst muss das Produkt aufgelöst werden, dann das Quadrat.
Indem du durch $3$ teilst, ergibt sich $9 = a^2$. Jetzt ziehst du noch die Quadratwurzel und erhältst die Ergebnisse $a_{1,2} = \pm 3$. Da du weißt, dass eine Streckenlänge nicht negativ sein kann, bleibt letztlich die Seitenlänge $a = 3$. Da $b = 3a$ ist, ergibt sich $b = 3 \cdot 3 = 9$.
Die gesuchten Seitenlängen sind also $a = 3~m$ und $b = 9~m$. Und tatsächlich ergibt die Probe, dass die Ausdrücke $a \cdot b = 3 \cdot 9 = 27$ und $A = 27$ übereinstimmen.
-
Ermittle die Seitenlängen des Zimmers.
TippsStelle zunächst fest, wie die beiden Seiten $a$ und $b$ zueinander stehen und ob sich eine Seite mithilfe der anderen ausdrücken lässt.
Bringe deine Gleichung in eine Form, auf welche sich die pq-Formel anwenden lässt.
LösungIn dieser Aufgabe geht es um die Aufstellung einer quadratischen Gleichung und die Anwendung der pq-Formel.
Peters Zimmer besitzt eine rechteckige Grundfläche und einen Flächeninhalt von $35~m^2 = a \cdot b$. Da er weiß, dass eine Seite zwei Meter länger ist als die andere, können wir sagen, dass $b = a + 2$.
Diese Information ist besonders wertvoll, da wir nun eine Gleichung aufstellen können, die nur eine Variable besitzt, nämlich $35 = a \cdot (a + 2) = a^2 + 2a$.
Wir erinnern uns, dass sich bei quadratischen Gleichungen die pq-Formel anwenden lässt. Dafür muss eine Gleichung die Form $a^2 + pa + q = 0$ haben. Das lässt sich auch bei unserer Gleichung herstellen. Dann haben wir $a^2 + 2a - 35 = 0$ mit $p = 2$ und $q = - 35$.
Jetzt kann die pq- Formel verwendet werden. Allgemein lautet sie:
$a_{1,2} = - \frac{p}{2} \pm \sqrt{ ( \frac{p}{2} )^2 - q}$.
Mit unseren Werten für p und q können wir schreiben:
$a_{1,2} = - \frac{2}{2} \pm \sqrt{ ( \frac{2}{2} )^2 + 35}$.
Wichtig ist hier, den Vorzeichenwechsel vor dem $q$ zu beachten. Darin liegt ein häufig praktizierter Fehler. Wenn wir nur $a_{1,2}$ berechnen, ergibt sich $a_1 = - 7$ und $a_2 = 5$. Das erste Ergebnis fällt weg, da eine Strecke keine negative Länge besitzen kann.
Die Seite $a$ ist also $5$ Meter lang, die Seite $b$ ist $7$ Meter lang. Die Probe bestätigt uns das Ergebnis, denn $a \cdot b = 5 \cdot 7 = 35$ und $A = 35$ stimmen überein.
-
Bestimme die Maße der $90~m^2$ großen rechteckigen Scheune, deren eine Seite um $8$ Meter länger ist als das Doppelte der anderen.
TippsDie allgemeine Gleichung, auf die du die pq-Formel anwenden kannst, lautet $x^2 + px + q = 0$. Der Faktor vor $x^2$ muss dabei $1$ sein.
Negative Lösungen fallen nach Anwendung der pq-Formel weg, wenn es um die Länge von Strecken geht.
LösungDie Scheune besitzt eine Fläche von $90~m^2$. Sie hat eine rechteckige Grundfläche und lässt sich dementsprechend mit der Formel $90 = a \cdot b$ berechnen. Die Seitenlängen $a$ und $b$ sind unbekannt, wir wissen aber, dass eine Seite um acht Meter länger als das Doppelte der anderen Seite ist. Es ist also, wenn wir $a$ als kürzere Seite festlegen, $b = 2a + 8$.
Damit können wir $b$ ersetzen und die Gleichung $90 = a \cdot (2a + 8)$ aufstellen. Lösen wir die Klammer auf, erhalten wir $90 = 2a^2 + 8a$. Um die pq-Formel verwenden zu können, müssen wir $90$ subtrahieren und dann durch $2$ teilen. Wir bekommen eine Gleichung der Form $a^2 + pa + q = 0$.
Das ist bei $a^2 + 4a - 45 = 0$ der Fall. Wir können die pq-Formel also mit $p = 4$ und $q = - 45$ anwenden. Wir setzen ein:
$\begin{align} a_{1,2} &= -\frac{4}{2}\pm \sqrt{ \left(\frac{4}{2}\right)^2+45} \\ &= - 2 \pm \sqrt{4 + 45} \\ &= - 2 \pm 7 \end{align}$
Es ergeben sich die Lösungen $a_1 = - 9$ und $a_2 = 5$. Als Lösung kommt nur $a = 5$ in Frage. Da der Zusammenhang zwischen $a$ und $b$ über $b = 2 \cdot a + 8$ gegeben ist, ergibt sich $b = 2 \cdot 5 + 8 = 18$.
Die Seitenlängen sind also $5$ und $18$ Meter lang. Die Probe bestätigt die Ergebnisse, denn die Ausdrücke $a \cdot b = 5 \cdot 18 = 90$ und $A = 90$ sind gleich.
-
Gib die wahren Aussagen zu quadratischen Gleichungen und Rechtecken an.
TippsIm Allgemeinen hat eine quadratische Funktion die Form f$($x$)$ = ax$^2$ + bx + c.
Die pq-Formel dient zum Lösen quadratischer Gleichungen.
LösungWie du an der allgemeinen quadratischen Funktion f$($x$)$ = ax$^2$ + bx + c sehen kannst, beträgt die höchste Potenz 2 bei x$^2$. Nur in diesem Fall ist von einer quadratischen Funktion die Rede.
f$($x$)$ = x$^3$ + 2x$^2$ oder f$($x$)$ = 4x + 3 sind keine quadratischen Funktionen.
In einem Rechteck sind die sich gegenüberliegenden Seiten gleich lang und ein Rechteck besitzt nur rechte Winkel als Innenwinkel. Eine Verlängerung der sich gegenüberliegenden Seiten würde keinen Schnittpunkt bewirken, da die Seiten parallel zueinander sind.
Die Verwendung der pq-Formel spielt beim Lösen von quadratischen Gleichungen eine wichtige Rolle. Du solltest beachten, dass deine Gleichung der Form x$^2$ + px + q = 0 entspricht, bevor du p und q in die Formel x$_{1,2}$ = - $\frac{\text{p}}{2}$ $\pm$ $\sqrt{ (\frac{\text{p}}{2})^2 - \text{q} }$ einsetzt.
Häufig kommen durch die pq-Formel auch negative Ergebnisse zustande. Wenn es um die Berechnung von Strecken geht, kannst du die negativen Ergebnisse vernachlässigen.
-
Ermittle die Längen der Katheten.
TippsWie kannst du Fläche eines Dreiecks bestimmen?
Berechne zuerst die Fläche des Rechtecks, welches die Katheten als Seiten hat und teile dein Ergebnis dann durch 2.
Bezeichne die kürzere Kathete mit a. Wie groß ist dann die längere Seite?
Negative Seitenlängen können nicht auftreten.
LösungHier suchen wir die Längen der Katheten in einem rechtwinkligen Dreiecks, dessen Flächeninhalt eine Größe von 6 cm$^2$ hat.
Wir wissen, dass der Flächeninhalt eines solchen Dreiecks sich durch A = $\frac{a \cdot b}{2}$ berechnen lässt. Wir tun einfach so, als wäre es ein Rechteck und teilen dann durch 2.
Wir wissen außerdem, dass die eine Kathete um $\frac{1}{3}$ länger als die andere ist. Bezeichnen wir die Länge der kürzeren Kathete mit a, dann hat die längere Kathete die Größe b = $\frac{4}{3} \cdot$ a.
Setzen wir in die Flächenformel ein und multiplizieren mit 2, so erhalten wir a $\cdot$ $\frac{4}{3}$ $\cdot$ a = 12. Wenn wir weiter auflösen, ergibt sich a$^2$ = 9 mit a$_{1,2}$ = $\pm$ 3.
Die kürzere Kathete a misst 3 cm, die längere b = $\frac{4}{3}$ a = 4 cm. Durch die Probe mit $\frac{a\cdot b}{2}$ = $\frac{3\cdot 4}{2}$ = 6 und A = 6 fühlen wir uns bestätigt.
9'204
sofaheld-Level
6'600
vorgefertigte
Vokabeln
7'650
Lernvideos
35'620
Übungen
32'360
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?


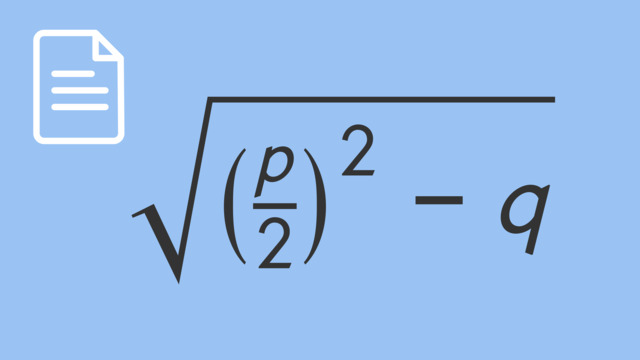









Danke für die genaue erklärung
Langsam und gut nachvollziehbar erklärt; ausgezeichnet!
Hans Scherer
Super erklärt! Vielen Dank :)