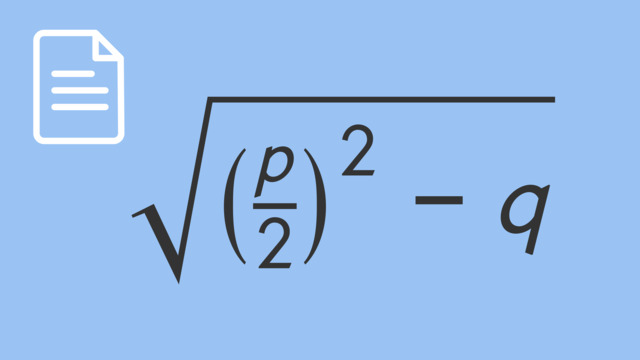Lösungsverhalten quadratischer Gleichungen – die Diskriminante
Mit der Diskriminante kannst du vorab die Anzahl der Lösungen einer quadratischen Gleichung herausfinden. Entdecke, wie du die pq-Formel anwendest und was die Diskriminante bedeutet. Neugierig? Lies weiter!
- Lösungsverhalten quadratischer Gleichungen – benötigtes Vorwissen
- Was ist die Diskriminante einer quadratischen Gleichung?
- Anzahl der Lösungen über die Diskriminante bestimmen
- Zwei Lösungen – Diskriminante > 0
- Eine Lösung – Diskriminante = 0
- Keine Lösung – Diskriminante < 0
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Lerntext zum Thema Lösungsverhalten quadratischer Gleichungen – die Diskriminante
Lösungsverhalten quadratischer Gleichungen – benötigtes Vorwissen
Du kennst vermutlich schon diverse Lösungswege für quadratische Gleichungen. Doch es gibt eine Möglichkeit, die Anzahl der Lösungen schon vor dem Berechnen dieser zu bestimmen. Das geht über die Diskriminante.
Für das Verstehen dieser Thematik musst du wissen, was eine quadratische Gleichung ist. Diese werden im Folgenden in ihrer Normalform zusammen mit der $pq$-Formel betrachtet. In diesem Text werden also Beispiele der Form $0 = x^{2} + px + q$ verwendet, um die Einbindung in die $pq$-Formel zu vereinfachen.
Was ist die Diskriminante einer quadratischen Gleichung?
Schauen wir uns zunächst den allgemeinen Fall (ohne konkrete Zahlenwerte) mit der $pq$-Formel an. Wir haben die quadratische Gleichung $0 = x^{2} + px + q$. Um diese zu lösen, können wir die $pq$-Formel anwenden:
$pq$-Formel:
$x_{1{,}2} = –\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^{2}~–~q}$
Diskriminante:
Den Term in der Wurzel, also $(\frac{p}{2})^{2}~–~q$, nennt man Diskriminante.
Anzahl der Lösungen über die Diskriminante bestimmen
Die Diskriminante ($\left(\frac{p}{2}\right)^{2}~–~q$) beschreibt den Term unterhalb der Wurzel in der $pq$-Formel. Weil das Wurzelziehen bestimmte mathematische Einschränkungen mit sich bringt, hat die Diskriminante einen direkten Einfluss auf die Anzahl an Lösungen für die quadratische Gleichung. Zum einen steht der Wurzelterm hinter dem $\pm$ und sorgt so dafür, dass es zwei Lösungen der Gleichung gibt, wenn der Wert der Diskriminante größer null ist. Zum anderen stellt die Wurzel aber auch die Ursache dar, wenn es für die quadratische Gleichung keine Lösung gibt. Wie das konkret aussieht, wird im Folgenden mithilfe von Beispielen gezeigt.
Zwei Lösungen – Diskriminante > 0
Wir betrachten die quadratische Gleichung $0 = x^{2} + 4x~–~5$. Damit ist $p = 4$ und $q = –5$. Die Werte werden in die $pq$-Formel eingesetzt:
$x_{1{,}2} = –\frac{4}{2} \pm \sqrt{(\frac{4}{2})^{2} + 5}$
Die Diskriminante ist damit der Term $(\frac{4}{2})^{2} + 5$. Dieser Term ist die Summe aus zwei positiven Zahlen und somit auf jeden Fall größer als $0$. Wir lösen die obige Gleichung.
$\begin{array}{rcccl} x_{1{,}2} & = & –\frac{4}{2} & \pm & \sqrt{(\frac{4}{2})^{2} + 5} \\ & = & –2 & \pm & \sqrt{2^{2} + 5} \\ & = & –2 \pm & \sqrt{9} \\ & = & –2 \pm & 3 \\ \end{array}$
$\Rightarrow x_1 = –2 + 3 = 1~\text{und}~x_2 = –2~–~3 = –5$
Diese Gleichung hat also zwei Lösungen. Woran liegt das? Wie oben beschrieben ist die Wurzel entscheidend. Da der Term unter der Wurzel positiv ist, erhalten wir bedingt durch das $\pm$ zwei unterschiedliche Lösungen. Die Wurzel wird zum $–\frac{p}{2}$ addiert und subtrahiert. Wir halten also fest:
Ist die Diskriminante einer quadratischen Gleichung größer als $0$, besitzt die quadratische Gleichung zwei Lösungen.
Eine Lösung – Diskriminante = 0
Wir betrachten die quadratische Gleichung $0 = x^{2} + 2x + 1$. Damit ist $p = 2$ und $q = 1$. Die Werte werden in die $pq$-Formel eingesetzt:
$x_{1{,}2} = –\frac{2}{2} \pm \sqrt{(\frac{2}{2})^{2}~–~1}$
Für die Diskriminante gilt damit: $(\frac{2}{2})^{2}~–~1 = 1~–~1 = 0$. Wir lösen die obige Gleichung.
$\begin{array}{rcccl} x_{1{,}2} & = & –\frac{2}{2} & \pm & \sqrt{(\frac{2}{2})^{2}~–~1} \\ & = & –1 & \pm & \sqrt{0} \\ & = & –1 & \pm & 0\\ \end{array}$
$\Rightarrow x_1 = –1 + 0 = –1~\text{und}~x_2 = –1~–~0 = –1$
Diese Gleichung hat also eine Lösung. Erneut ist die Wurzel und damit die Diskriminante verantwortlich dafür. Da der Term unter der Wurzel $0$ ist, wird zum Term $–\frac{p}{2}$ weder etwas addiert noch subtrahiert. Wir halten also fest:
Ist die Diskriminante einer quadratischen Gleichung gleich $0$, besitzt die quadratische Gleichung eine Lösung.
Keine Lösung – Diskriminante < 0
Wir betrachten die quadratische Gleichung $0 = x^{2} + 4x + 5$. Damit ist $p = 4$ und $q = 5$. Die Werte werden in die $pq$-Formel eingesetzt:
$x_{1{,}2} = –\frac{4}{2} \pm \sqrt{(\frac{4}{2})^{2}~–~5}$
Die Diskriminante ist damit der Term $(\frac{4}{2})^{2}~–~5 = 4~–~5$. Dieser Term ist auf jeden Fall kleiner als $0$. Wir lösen die obige Gleichung.
$\begin{array}{rcccl} x_{1{,}2} & = & –\frac{4}{2} & \pm & \sqrt{(\frac{4}{2})^{2}~–~5} \\ & = & –2 & \pm & \sqrt{4~–~5} \\ & = & –2 \pm & \sqrt{–1} \\ \end{array}$
Die Wurzel $\sqrt{–1}$ können wir nicht ziehen, da es innerhalb der reellen Zahlen nicht möglich ist, die Wurzel aus negativen Zahlen zu ziehen. Diese Gleichung hat also keine Lösungen. Da der Term unter der Wurzel negativ ist, lässt sich die Wurzel nicht ziehen. Wir halten also fest:
Ist die Diskriminante einer quadratischen Gleichung kleiner als $0$, besitzt die quadratische Gleichung keine Lösung.
Quadratische Gleichungen mit Parametern
Im Zusammenhang mit der Anzahl der möglichen Lösungen von quadratischen Gleichungen können dir auch Aufgaben mit Parametern begegnen. Deswegen wollen wir dies im Folgenden an einem Beispiel erläutern.
Parameter sind Variablen, die mit anderen Variablen kombiniert auftreten. Dabei sind Parameter im Gegensatz zu den anderen Variablen für den jeweils betrachteten Fall festgelegt. Ein einfaches Beispiel ist die allgemeine lineare Funktionsgleichung $y = m \cdot x + b$, in der $m$ und $b$ Parameter und $x$ und $y$ Variablen sind.
Wir betrachten die quadratische Gleichung $0 = x^{2}~–~2ax + 2a + 3$. Um nun bestimmen zu können, für welche Werte des Parameters $a$ die Gleichung zwei Lösungen, eine oder keine Lösung besitzt, schauen wir uns die Diskriminante der Gleichung an. Dazu stellen wir die $pq$-Formel mit $p = –2a$ und $q = 2a + 3$ auf.
$x_{1{,}2} = –\frac{–2a}{2} \pm \sqrt{(\frac{–2a}{2})^{2}~–~(2a + 3)}$
Um herauszufinden, für welche Werte von $a$ die Gleichung zwei Lösungen, eine oder keine Lösung hat, brauchen wir uns nun nur die Diskriminante $(\frac{–2a}{2})^{2}~–~(2a + 3)$ anzuschauen. Also vereinfachen wir:
$(\frac{–2a}{2})^{2}~–~(2a + 3) = (–a)^{2}~–~2a~–~3 = a^{2}~–~2a~–~3$
Diese Diskriminante muss für zwei Lösungen $> 0$, für eine Lösung $= 0$ und für keine Lösung $< 0$ sein. Ungleichungen sind immer etwas schwierig, also schauen wir uns an, für welche Werte von $a$ die Gleichung $= 0$ wird. Wir wollen also die Gleichung $0 = a^{2}~–~2a~–~3$ lösen, was wiederum eine quadratische Gleichung ist, die wir mit der $pq$-Formel lösen können:
$\begin{array}{rcccl} a_{1{,}2} & = & –\frac{–2}{2} & \pm & \sqrt{(\frac{–2}{2})^{2} + 3} \\ & = & 1 & \pm & \sqrt{1 + 3} \\ & = & 1 \pm & \sqrt{4} \\ & = & 1 \pm & 2 \end{array}$
$\Rightarrow a_1 = 1 + 2 = 3 \text{ und } a_2 = 1~–~2 = –1$
Also wird die Diskriminante unserer quadratischen Gleichung für $a_1 = 3$ und $a_2 = –1$ zu $0$. Das bedeutet auch, dass für diese Werte die quadratische Gleichung $0 = x^{2} –2ax + 2a + 3$ nur eine Lösung hat.
Um nun noch herauszufinden, für welche Werte von $a$ die Gleichung keine oder zwei Lösungen hat, müssen wir uns die Intervalle anschauen, die sich um die Nullstellen ergeben. Diese lauten anhand der obigen Werte:
- $a < –1$
- $–1 < a < 3$
- $a > 3$
Dafür setzen wir entsprechende Werte aus diesen Intervallen für $a$ in unsere Diskriminante $a^{2}~–~2a~–~3$ ein. Innerhalb eines Intervalls ist die Diskriminante für alle Werte von $a$ positiv ($>0$) oder für alle Werte von $a$ negativ ($<0$). Daher reicht es, einen beliebigen Wert pro Intervall für $a$ einzusetzen.
- $a = –2 \Rightarrow (–2)^{2}~–~2 \cdot (–2)~–~3 = 4 + 4~–~3 = 5 > 0$
Für $a < –1$ hat die quadratische Gleichung also zwei Lösungen, da die Diskriminante in diesem Intervall positiv ist.
- $a = 0 \Rightarrow (0)^{2}~–~2 \cdot (0)~–~3 = –3 < 0$
Also hat die Gleichung für $–1 < a < 3$ keine Lösungen, da die Diskriminante in diesem Intervall negativ ist.
- $a = 4 \Rightarrow 4^{2}~–~2 \cdot 4~–~3 = 16~–~8~–~3 > 0$
Und zuletzt hat die Gleichung auch für $a > 3$ zwei Lösungen, da die Diskriminante in diesem Intervall positiv ist.
Zusammenfassung – Lösungsverhalten quadratischer Gleichungen
Wenn vor der endgültigen Berechnung Aussagen darüber getroffen werden sollen, wie viele mögliche Lösungen eine quadratische Gleichung hat, kann dies über die Diskriminante gemacht werden. Es handelt sich dabei um den Term unter der Wurzel in der $pq$-Formel, also um den Term $(\frac{p}{2})^{2}~–~q$ bei der quadratischen Gleichung $0 = x^{2} + px + q$. Es gilt:
- $(\frac{p}{2})^{2}~–~q > 0 \Rightarrow$ Die Gleichung hat zwei Lösungen.
- $(\frac{p}{2})^{2}~–~q = 0 \Rightarrow$ Die Gleichung hat eine Lösung.
- $(\frac{p}{2})^{2}~–~q < 0 \Rightarrow$ Die Gleichung hat keine Lösung.
Dies ist insbesondere beim Rechnen mit Parametern nützlich.
Häufig gestellte Fragen zum Thema Lösungsverhalten von quadratischen Gleichungen
Lösungsverhalten quadratischer Gleichungen – die Diskriminante Übung
-
Welche Aussagen zum Lösungsverhalten quadratischer Gleichungen sind richtig?
TippsZwei Aussagen sind richtig.
LösungBei der Diskriminante handelt es sich um den Term unter der Wurzel in der $pq$-Formel, also um den Term $(\frac{p}{2})^{2}~–~q$.
Die Anzahl der Lösungen einer Gleichung ist abhängig davon, ob die Diskriminante größer, kleiner oder gleich $0$ ist.
-
Welche Aussagen gehören zusammen?
TippsEs geht darum, ob die Diskriminante kleiner, gleich oder größer als 0 ist.
Lösung$(\frac{p}{2})^{2}~–~q > 0 \Rightarrow$ Die Gleichung hat zwei Lösungen.
$(\frac{p}{2})^{2}~–~q = 0 \Rightarrow$ Die Gleichung hat eine Lösung.
$(\frac{p}{2})^{2}~–~q < 0 \Rightarrow$ Die Gleichung hat keine Lösungen.
-
Wie viele Lösungen hat die Gleichung?
Tipps$(\frac{p}{2})^{2}~–~q > 0 \Rightarrow$ Die Gleichung hat zwei Lösungen.
$(\frac{p}{2})^{2}~–~q = 0 \Rightarrow$ Die Gleichung hat eine Lösung.
$(\frac{p}{2})^{2}~–~q < 0 \Rightarrow$ Die Gleichung hat keine Lösungen.
LösungWir betrachten die quadratische Gleichung $0 = x^{2} + 4x~–~5$.
Damit ist $p = 4$ und $q = –5$.
Die Werte werden in die $pq$-Formel eingesetzt:
$x_{1{,}2} = –\frac{4}{2} \pm \sqrt{(\frac{4}{2})^{2} + 5}$
Die Diskriminante ist der Term $(\frac{4}{2})^{2} + 5$.
Dieser Term ist größer als $0$.
<p>$\begin{array}{rcccl} x_{1{,}2} & = & –\frac{4}{2} & \pm & \sqrt{(\frac{4}{2})^{2} + 5} \\ & = & –2 & \pm & \sqrt{2^{2} + 5} \\ & = & –2 \pm & \sqrt{9} \\ & = & –2 \pm & 3 \\ \end{array}$</p>
$\Rightarrow x_1 = –2 + 3 = 1~\text{und}~x_2 = –2~–~3 = –5$
Diese Gleichung hat also zwei Lösungen.
-
Wie viele Lösungen haben die quadratischen Gleichungen?
Tipps$(\frac{p}{2})^{2}~–~q > 0 \Rightarrow$ Die Gleichung hat zwei Lösungen.
$(\frac{p}{2})^{2}~–~q = 0 \Rightarrow$ Die Gleichung hat eine Lösung.
$(\frac{p}{2})^{2}~–~q < 0 \Rightarrow$ Die Gleichung hat keine Lösungen.
Lösung$2$ Lösungen:
$x_{1{,}2} = –\frac{4}{2} \pm \sqrt{(\frac{4}{2})^{2} + 5}$
$x_{1{,}2} = –\frac{9}{2} \pm \sqrt{(\frac{9}{2})^{2} + 14}$
$1$ Lösung:
$x_{1{,}2} = –\frac{2}{2} \pm \sqrt{(\frac{2}{2})^{2}~–~1}$
$x_{1{,}2} = –\frac{4}{2} \pm \sqrt{(\frac{4}{2})^{2}~–~4}$
$0$ Lösungen:
$x_{1{,}2} = –\frac{6}{2} \pm \sqrt{(\frac{6}{2})^{2}~–~22}$
$x_{1{,}2} = –\frac{4}{2} \pm \sqrt{(\frac{4}{2})^{2}~–~5}$
-
Finde die Fehler in der Rechnung.
TippsVier Stellen müssen markiert werden.
LösungWir betrachten die quadratische Gleichung $0 = x^{2} + 6x + 21$.
Damit ist $p = 6$ und $q = 21$.
Die Werte werden in die $pq$-Formel eingesetzt:
$x_{1{,}2} = –\frac{6}{2} \pm \sqrt{(\frac{6}{2})^{2}~–~21}$
Die Diskriminante ist damit der Term $(\frac{6}{2})^{2}~–~21 = 9~–~21$.
Dieser Term ist kleiner als $0$.
Wir lösen die obige Gleichung.
<p>$\begin{array}{rcccl} x_{1{,}2} & = & –\frac{6}{2} & \pm & \sqrt{(\frac{6}{2})^{2}~–~21} \\ & = & –3 & \pm & \sqrt{9~–~21} \\ & = & –3 \pm & \sqrt{–12} \\ \end{array}$</p>
Die Wurzel $\sqrt{–12}$ können wir nicht ziehen, da es innerhalb der reellen Zahlen nicht möglich ist, die Wurzel aus negativen Zahlen zu ziehen.
Diese Gleichung hat also keine Lösungen.
-
Für welche Parameter von $a$ hat die Gleichung eine Lösung?
TippsParameter sind Variablen, die mit anderen Variablen kombiniert auftreten. Dabei sind Parameter im Gegensatz zu den anderen Variablen für den jeweilig betrachteten Fall festgelegt. Ein einfaches Beispiel ist die allgemeine lineare Funktionsgleichung $y = m \cdot x + b$, in der $m$ und $b$ Parameter und $x$ und $y$ Variablen sind.
LösungWir betrachten die quadratische Gleichung $0 = x^{2}~–~2ax + 4a + 5$.
Um bestimmen zu können, für welche Werte des Parameters $a$ die Gleichung eine Lösung besitzt, schauen wir uns die Diskriminante der Gleichung an.
Dazu stellen wir die $pq$-Formel mit $p = –2a$ und $q = 4a + 5$ auf.
$x_{1{,}2} = –\frac{–2a}{2} \pm \sqrt{(\frac{–2a}{2})^{2}~–~(4a + 5)}$
Wir vereinfachen die Diskriminante:
$(\frac{–2a}{2})^{2}~–~(4a + 5) = (–a)^{2}~–~4a~–~5 = a^{2}~–~4a~–~5$
Diese Diskriminante muss für eine Lösung $= 0$ sein.
Wir wollen also die Gleichung $0 = a^{2}~–~4a~–~5$ lösen, was wiederum eine quadratische Gleichung ist, die wir mit der $pq$-Formel lösen können:
<p>$\begin{array}{rcccl} a_{1{,}2} & = & –\frac{–4}{2} & \pm & \sqrt{(\frac{–4}{2})^{2} + 5} \\ & = & -2 & \pm & \sqrt{4 + 5} \\ & = & -2 \pm & \sqrt{9} \\ & = & -2 \pm & 3 \end{array}$</p> $\Rightarrow a_1 = -2+3 = 1 \text{ und } a_2 = -2-3 = –5$
Also wird die Diskriminante unserer quadratischen Gleichung für $a_1 = 1$ und $a_2 = –5$ zu $0$.
Das bedeutet auch, dass für diese Werte die quadratische Gleichung $0 = x^{2} –2ax + 4a + 5$ nur eine Lösung hat.
9'908
sofaheld-Level
6'600
vorgefertigte
Vokabeln
7'804
Lernvideos
37'196
Übungen
32'654
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?