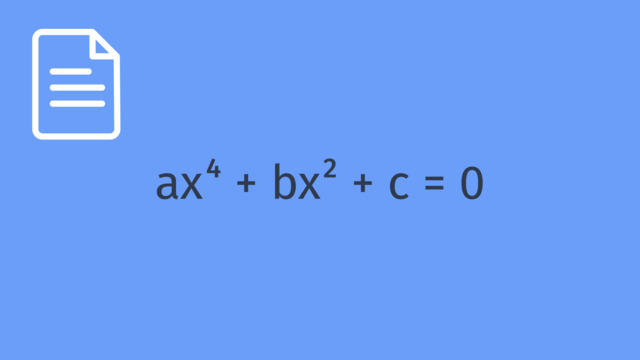Gleichungen 3. Grades ohne Absolutglied – Ausklammern

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Gleichungen 3. Grades ohne Absolutglied – Ausklammern
Nach dem Schauen dieses Videos wirst du in der Lage sein, Gleichungen 3. Grades ohne Absolutglied zu lösen.
Zunächst lernst du, was eine Gleichung 3. Grades ist und welche Eigenschaften diese hat. Anschließend lernst du, wie viele Lösungen diese Gleichung haben kann. Abschließend lernst du, eine Gleichung 3. Grades ohne Absolutglied mithilfe der pq-Formel und des Satzes vom Nullprodukt zu lösen.
Lerne etwas über Gleichungen 3. Grades ohne Absolutglied, während du Alice Kubinski, Spionin 3. Grades, bei ihren Recherchen begleitest.
Das Video beinhaltet Schlüsselbegriffe, Bezeichnungen und Fachbegriffe wie Gleichungen, Kubische Gleichung, Satz vom Nullprodukt, pq-Formel und Ausklammern.
Bevor du dieses Video schaust, solltest du bereits wissen, wie du Gleichungen 2. Grades löst.
Nach diesem Video wirst du darauf vorbereitet sein, das Lösen von Gleichungen 3. Grades mit Absoluglied zu lernen.
Transkript Gleichungen 3. Grades ohne Absolutglied – Ausklammern
Oh Mann, was für ein Mistwetter! Alice Kubinski, Spionin 3. Grades ist im Einsatz und beobachtet die seltsamen Machenschaften zweier verdächtiger Subjekte. Was ist das?! Vermutlich ein verschlüsselter Hinweis zu einem geheimen Treffpunkt! Alice braucht Hilfe und wird von ihrem Informanten kontaktiert. Aha, diese seltsamen Gleichungen sind also Gleichungen 3. Grades ohne Absolutglied! Was ist überhaupt eine Gleichung dritten Grades? Hier siehst du eine in allgemeiner Form. "x hoch 3" ist in dieser Gleichung die höchste Potenz von x - und genau darauf bezieht sich die Bezeichnung "3. Grades". Man nennt solche Gleichungen auch kubische Gleichung. Die einzelnen Bestandteile werden als kubisches Glied quadratisches Glied, lineares Glied und absolutes Glied bezeichnet. Der Koeffizient a darf bei solchen Gleichungen nicht 0 sein, sonst gäbe es das kubische Glied nicht. Es gibt einen Spezialfall: Wenn d gleich Null ist, dann liegt eine kubische Gleichung ohne Absolutglied vor. Glück für Alice! Denn Gleichungen 3. Grades ohne Absolutglied sind etwas einfacher zu lösen. Eine Gleichung dritten Grades hat für reelle x-Werte übrigens immer mindestens eine Lösung aber maximal drei! Alice will natürlich alle möglichen Lösungen bestimmen! Und zum Glück kommt da schon ein wichtiger Hinweis von ihrem Informanten! Schauen wir uns das mal genauer an. Scheinbar sollen wir x ausklammern und den Satz vom Nullprodukt anwenden: Der lautet: Ein Produkt ist Null, wenn einer der Faktoren Null ist. Wir haben zwar in unserer Gleichung auf der einen Seite eine Null aber das hier ist ja kein Produkt! In jedem Term steckt jedoch mindestens ein x, also können wir x ausklammern! Dann haben wir ein Produkt, das Null ergibt! Nach dem Satz vom Nullprodukt ist die Gleichung also erfüllt, wenn entweder dieser Faktor, also das x, gleich Null ist oder dieser quadratische Ausdruck gleich Null ist. Und daraus ermitteln wir dann jeweils die Lösungen! Starten wir mit dem Lösen der ersten Gleichung! Da x in jedem Term auf der linken Seite der Gleichung vorkommt, können wir das x ausklammern. Ganz wie geplant! Jetzt nutzen wir den Satz vom Nullprodukt: Ein Produkt ist Null, wenn einer der Faktoren Null ist. Also ist die Gleichung erfüllt, wenn x selbst Null ist. Dies ist die erste Lösung der kubischen Gleichung. Die Gleichung ist aber auch erfüllt, wenn der verbliebene quadratische Term gleich null ist. Für die möglichen weiteren Lösungen müssen wir also diese Gleichung lösen zum Beispiel mit der pq-Formel. Dazu müssen wir erstmal die 5 vor dem x² loswerden, also teilen die gesamte Gleichung durch 5. Dann können wir p und q bestimmen. Jetzt setzen wir die Zahlen für p und q in die pq-Formel ein vereinfachen. Diese Vorzeichen heben sich gegenseitig auf, in Klammern minus ein Halb zum Quadrat ergibt 1 Viertel, und Minus in Klammern minus 2 ergibt plus 2. 2 schreiben wir als 8 Viertel und fassen unter der Wurzel zusammen. Jetzt noch die Wurzel ziehen und wir erhalten durch das plus minus die zwei weiteren Lösungen. Alle Lösungen, x1 gleich 0, x2 gleich 2 und x3 gleich -1, halten wir in der Lösungsmenge fest. Nun müssen wir nur noch die zweite Gleichung lösen! Bevor wir loslegen können, bringen wir die Gleichung in ihre allgemeine Form. Dafür ziehen wir 24 auf beiden Seiten der Gleichung ab, damit hinter dem Gleichheitszeichen nur noch eine Null steht. Jetzt klammern wir wieder das x aus! Durch den Satz vom Nullprodukt wissen wir, dass entweder x Null sein muss oder dieser quadratische Term. Zur Lösung der entsprechenden quadratischen Gleichung brauchen wir diesmal die p-q-Formel nicht! Bringen wir hier die 4 auf die andere Seite der Gleichung und entfernen vom "x Quadrat" noch den störenden Faktor, dann müssen wir nur noch die Wurzel ziehen, um die möglichen Lösungen zu erhalten! Aber aus einer negativen Zahl dürfen wir die Wurzel nicht ziehen, weshalb x2 und x3 nicht definiert sind. Die kubische Gleichung hat hier also nur eine Lösung, nämlich x1 gleich null. Nun noch einmal alles in der Zusammenfassung. Eine Gleichung dritten Grades ohne Absolutglied erkennst du daran, dass die höchste Potenz "x hoch drei" ist und kein abolutes Glied vorkommt. Um die Lösungsmenge zu bestimmen, klammerst du erstmal ein x aus. Nach dem Satz vom Nullprodukt ist die erste Lösung "x Eins" gleich Null. Der quadratische Faktor liefert dann bis zu zwei weiteren Lösungen. Abschließend können wir die Lösungsmenge angeben. Alice hat ganze Arbeit geleistet und den geheimen Treffpunkt mit Hilfe der Lösungen gefunden! Sie klopft. Ein bisschen mulmig ist ihr schon. Was ist denn hier los? Eine geheime Mathelehrer-Party?! Manche Sachen will man einfach nicht über seine Mathelehrer wissen.
Gleichungen 3. Grades ohne Absolutglied – Ausklammern Übung
-
Bestimme die korrekten Aussagen zu Gleichungen dritten Grades.
TippsEin Produkt ist das Ergebnis einer Multiplikation. Die beiden Zahlen, die multipliziert werden, heißen Faktoren. Also:
$\text{Faktor} \cdot \text{Faktor}= \text{Produkt}$
Multiplizierst du eine Zahl mit null, ist das Ergebnis immer gleich null!
LösungDiese Aussagen sind falsch:
- „Gleichungen, deren Variablen höchstens zur dritten Potenz erhoben sind, heißen quadratische Gleichungen.“
- „Eine Gleichung dritten Grades kann nur entweder keine oder drei reelle Lösungen haben.“
Diese Aussagen sind richtig:
- „Das Absolutglied einer Gleichung ist der Teil, der nicht mit einer Variablen multipliziert wird.“
- „Bei einer Gleichung dritten Grades ohne Absolutglied musst du zuerst $x$ ausklammern, um den Satz vom Nullprodukt anwenden zu können.“
- „Der Satz vom Nullprodukt besagt, dass ein Produkt genau dann gleich null wird, wenn einer seiner Faktoren null ist.“
-
Bestimme die Lösung der Gleichung dritten Grades.
TippsIn einer Gleichung in Normalform stehen alle Terme der Gleichung auf einer Seite. Durch Äquivalenzumformungen kannst du Gleichungen auf die Normalform bringen. Zum Beispiel steht
$x^2=4$
nicht in der Normalform. Ziehst du $4$ von der Gleichung ab, ist sie in der Normalform:
$ x^2-4=0$
Die Quadratwurzel einer negativen Zahl ist im reellen Zahlenraum nicht definiert.
LösungDen Lückentext kannst du so vervollständigen:
„Zuerst bringt sie die Gleichung auf die Normalform. Dazu zieht sie auf beiden Seiten $24$ ab. Dann erhält sie:
$-9x^3-4x=0$.“
- In einer Gleichung in Normalform stehen alle Terme der Gleichung auf einer Seite. Durch Äquivalenzumformungen kannst du Gleichungen auf die Normalform bringen.
$x \cdot (-9x^2-4)=0$.“
- Um den Satz vom Nullprodukt anwenden zu können, musst du die Gleichung zuerst in ein Produkt umformen. Das erreichst du, indem du $x$ ausklammerst.
- Setzt du $0$ in die Gleichung ein, dann wird die Gleichung gleich $0$. Denn alles, was mit null multipliziert wird, wird zu null.
$-9x^2-4=0$.“
- Jetzt musst du herausfinden, wann der andere Faktor der Gleichung gleich null wird. Das erreichst du, indem du ihn gleich null setzt.
$x^2= -\frac{4}{9}$.
Diese Gleichung ist nicht lösbar. Damit beträgt die Lösungsmenge: $\mathrm{L}=\{x=0\}$.“
- Die Quadratwurzel eine negativen Zahl ist im reellen Zahlenraum nicht definiert. Deshalb hat diese Gleichung nur die Lösung $x=0$.
-
Ermittle die Lösung der Gleichungen.
TippsDu kannst die Lösungen der Gleichungen bestimmen, indem du die Gleichungen faktorisierst und den Satz vom Nullprodukt verwendest.
Bleibt nach dem Faktorisieren eine quadratische Gleichung, kannst du diese mit der $p-q-Formel$ oder Mitternachtsformel lösen.
LösungVerbinde die Gleichungen mit ihren Lösungen, indem du die Gleichungen faktorisierst und den Satz vom Nullprodukt verwendest. Bei
$x^3-4x=0$
kannst du folgendermaßen vorgehen:
$\begin{array}{ll} x^3-4x&=0 \\ x(x^2-4)&=0 \end{array}$
Daraus folgt die erste Lösung der Gleichung: $x_2=0$. Die anderen kannst du bestimmen, indem du den zweiten Faktor gleich null setzt:
$\begin{array}{lll} x^2-4&=0 &\vert+4\\ x^2&=4 &\vert\sqrt{\hphantom{x}}\\ x&= \pm 2 \end{array}$
Daraus folgen die anderen beiden Lösungen: $x_1=-2$ und $x_3=2$. Die Nummerierung der Lösungen ist beliebig wählbar.
Die anderen Gleichungen kannst du analog lösen. Dann erhältst du:
- $3x^3-27x=0$ hat die Lösungen $x_1=-3$, $x_2=0$, $x_3=3$
- $x^3-x^2-6x=0$ wir durch $x_1=-2$, $x_2=0$, $x_3=3$ gelöst
- $5x^3-5x=0$ ergibt: $x_1=-1$, $x_2=0$, $x_3=1$
-
Leite die Lösungen der Gleichungen her.
TippsBetrachtest du ein Produkt aus zwei Faktoren, dann besagt der Satz vom Nullprodukt, dass das Produkt genau dann gleich null ist, wenn einer der Faktoren gleich null ist.
LösungBestimme die Lösungen der Gleichungen mit dem bekannten Vorgehen. Für die erste Gleichung erhältst du:
$\begin{array}{lll} x^3+2x+15&=15 &\vert -15\\ x^3+2x&=0 \\ x(x^2+2)&=0\\ \end{array}$
Daraus folgt die erste Lösung der Gleichung: $x_2=0$. Die anderen kannst du bestimmen, indem du den zweiten Faktor gleich null setzt:
$\begin{array}{lll} x^2+2&=0 & \vert -2\\ x^2 &=-2 \end{array}$
Diese Gleichung hat keine Lösung, da die Wurzel einer negativen Zahl nicht definiert ist. Die anderen Gleichungen kannst du auf ähnliche Weise lösen. Dann erhältst du:
- $x^3+3x^2-10x=0$ hat die Lösungen $x_1=-5$ $x_2=0$ und $x_3=2$
- $(x^2-9)x+13=13$ ergibt $x_1=-3$, $x_2=0$ und $x_3=3$
- Die Gleichung $3x^3-60x=15x$ wird gelöst durch $x_1=-5$, $x_2=0$ und $x_1=5$
- $3x^3-24x^2 +45x=0$ hat folgende Lösungen $x_1=0$, $x_2=3$ und $x_3=5$
-
Benenne die Teile der kubischen Gleichung.
TippsDie Potenz der Variablen entscheidet über den Namen des Glieds.
In quadratischen Gliedern ist die Variable zur zweiten Potenz erhoben.
LösungDu kannst die Glieder folgendermaßen zuordnen:
- In kubischen Gliedern ist die Variable zur dritten Potenz erhoben: $-9x^3$, $5x^3$ und $ax^3$
- In quadratischen Gliedern ist die Variable zur zweiten Potenz erhoben: $bx^2$, $-5x^2$
- In linearen Gliedern ist die Variable zur ersten Potenz erhoben: $cx$ und $-10x$
- Absolutglieder stehen ohne Variable: $-10$ und $d$
-
Erschließe eine Nullstelle der Gleichungen dritten Grades mit Absolutglied.
TippsHier geht es darum, die erste Nullstelle zu erraten. Dabei kannst du ausnutzen, dass das Absolutglied durch diese Nullstelle teilbar sein muss. Du kannst also alle Teiler des Absolutglieds nacheinander in die Gleichung einsetzen und überprüfen, ob sie die Gleichung lösen.
Das Absolutglied von
$x^3+6x^2+11x+6=0$
ist beispielsweise durch die Zahlen $\pm1$, $\pm2$, $\pm3$ und $\pm6$ teilbar. Setze nacheinander alle diese Zahlen in die Gleichung ein und überprüfe, ob sie die Gleichung lösen.
LösungHier geht es darum, die erste Nullstelle zu erraten. Dabei kannst du ausnutzen, dass das Absolutglied durch die Nullstellen teilbar sein muss. Du kannst also alle Teiler des Absolutglieds nacheinander in die Gleichung einsetzen und überprüfen, ob sie die Gleichung lösen.
Die Gleichung $x^3-x^2+x-1=0$ hat das Absolutglied $-1$. Es ist durch $-1$ und $1$ vollständig teilbar. Setzt du $-1$ in die Gleichung ein, erhältst du:
$(-1)^3-(-1)^2+(-1)-1=-1-1-1-1=-4 \neq 0$
Die Gleichung wird also nicht durch $-1$ gelöst. Setzt du die andere Möglichkeit $1$ ein, erhältst du:
$1^3-1^2+1-1=0$
$x=1$ löst also die Gleichung. So kannst du auch die Nullstellen der anderen Gleichungen bestimmen, wobei es jeweils ausreicht, eine der möglichen Lösungen zu finden. Du erhältst:
- Die Gleichung $x^3-x^2-3x-1=0$ hat eine Nullstelle bei $x=-1$.
- Die Nullstellen von $x^3+6x^2+11x+6=0$ liegen bei $x=-1$, $x=-2$ oder $x=-3$.
- $3x^3+4x^2-x+6=0$ hat eine Nullstelle bei $x=-2$.
- Die Gleichung $-x^3+3x^2+x-3=0$ hat Nullstellen bei $x=3$, $x=-1$ und $x=1$.
9'182
sofaheld-Level
6'600
vorgefertigte
Vokabeln
7'643
Lernvideos
35'607
Übungen
32'360
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?