Spurpunkte von Geraden und Schatten
Beim Billardspiel bewegt sich eine Kugel modellhaft entlang einer Geraden. Dabei trifft sie an verschiedenen Punkten auf die Bande, den Rand des Billardtisches. Mathematisch werden diese Punkte als Spurpunkte bezeichnet.
Beliebteste Videos
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was ist ein Spurpunkt?
Ein Spurpunkt ist ein Schnittpunkt einer Geraden mit einer der Koordinatenebenen. Du musst also einen Punkt auf der Geraden finden, welcher auch gleichzeitig in einer der Koordinatenebenen liegt. Eine besondere Rolle spielen diese Spurpunkte beim Schattenwurf.
Hierfür wiederholen wir zunächst einmal, was Geraden im dreidimensionalen Raum und was Koordinatenebenen sind.
Geraden im Raum
Eine Gerade $g$ im dreidimensionalen Raum sieht so aus:
$g:\vec x=\vec a+r\cdot \vec u$.
Diese Darstellung wird Parameterform oder auch Parametergleichung genannt. Die darin enthaltenen Größen haben die folgende Bedeutung:
- $\vec x$ ist ein Vektor, der auf einen beliebigen Punkt der Geraden zeigt.
- $\vec a$ ist der sogenannte Stützvektor. Dieser zeigt auf einen bekannten Punkt der Geraden.
- $\vec u$ ist ein Richtungsvektor der Geraden.
- $r$ ist ein Parameter.
Die Koordinatenebenen
In einem $x$-$y$-$z$-Koordinatensystem gibt es drei Koordinatenebenen:
- Die $x$-$y$-Koordinatenebene: Jeder Punkt dieser Ebene hat die $z$-Koordinate $z=0$.
- Die $x$-$z$-Koordinatenebene: Jeder Punkt dieser Ebene hat die $y$-Koordinate $y=0$.
- Die $y$-$z$-Koordinatenebene: Jeder Punkt dieser Ebene hat die $x$-Koordinate $x=0$.
Entsprechend dieser Ebenen werden die Spurpunkte oft mit Indices benannt. Zum Beispiel ist $S_{xy}$ der Spurpunkt mit der $x$-$y$-Koordinatenebene.
Schattenwurf
Wir schauen uns als Beispiel den Schatten an, den ein schwebender Würfel auf den Boden wirft. Der Schatten des Würfels soll in der $x$-$y$-Koordinatenebene liegen. Hier siehst du den sogenanntenSchattenpunkt eines Eckpunktes des Würfels in der $x$-$y$-Ebene bei einer gegebenen punktförmigen Lichtquelle. Der Schattenpunkt ist die Projektion eines Punktes auf eine Fläche, in diesem Fall die $x$-$y$-Ebene.
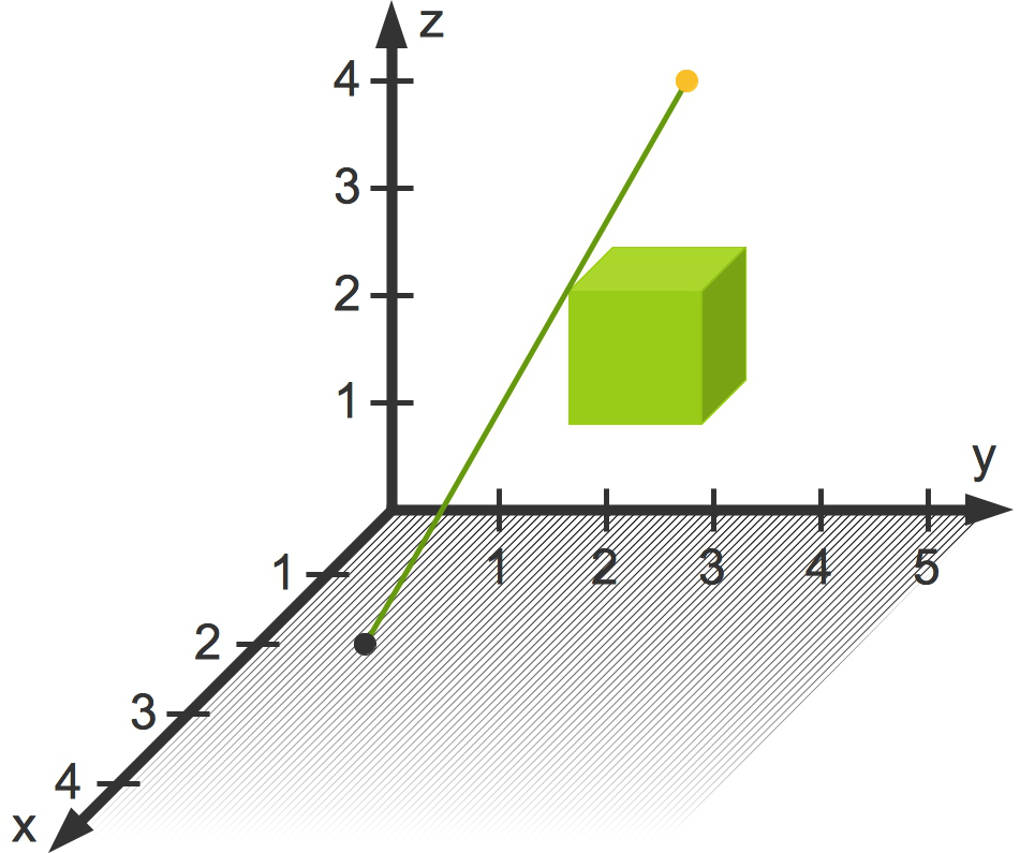
Bestimmung eines Spurpunktes
Wie kann man einen Spurpunkt berechnen? Wir schauen uns dies an dem obigen Beispiel an. Die Lichtquelle liegt im Punkt $L(2|4|6)$. Der Eckpunkt des Würfels sei $A(2|3|4)$.
Zunächst stellst du die Gleichung der Geraden auf, welche durch diese beiden Punkte verläuft.
- Hierfür wählst du den Ortsvektor eines der beiden Punkte als Stützvektor.
- Der Verbindungsvektor der beiden Punkte ist der Richtungsvektor der Geraden. Du erhältst den Verbindungsvektor zweier Punkte, indem du von dem Ortsvektor des Endpunktes den des Anfangspunktes subtrahierst.
$g:\vec x=\begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix}+r\cdot \begin{pmatrix} 0 \\ -1 \\ -2 \end{pmatrix}$
Der Spurpunkt dieser Geraden mit der $x$-$y$-Koordinatenebene hat die $z$-Koordinate $z=0$.
Die $z$-Koordinate eines beliebigen Punktes der Geraden lautet $z=6-2r$. Du löst also die Gleichung $6-2r=0$:
- Addiere zunächst $2r$. So erhältst du die Gleichung $2r=6$.
- Nun dividierst du durch $2$ und erhältst $r=3$.
Zuletzt setzt du diesen Wert für den Parameter $r$ in die Geradengleichung ein und gelangst so zu dem Ortsvektor des Spurpunktes:
$\vec{s_{xy}}=\begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix}+3\cdot \begin{pmatrix} 0 \\ -1 \\ -2 \end{pmatrix}=\begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix}+\begin{pmatrix} 0 \\ -3 \\ -6 \end{pmatrix}=\begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}$
Der Spurpunkt ist somit $S_{xy}(2|1|0)$.
Lagebeziehungen Gerade und deren Spurpunkte
Im Folgenden wirst du an Beispielen zum einen noch einmal sehen, wie die Spurpunkte berechnet werden, und zum anderen, welche spezielle Lage eine Gerade im Raum haben kann.
Spurpunkte in jeder Koordinatenebene des dreidimensionalen Raumes
Die Gerade $g$ sei wie folgt gegeben:
$g:\vec x=\begin{pmatrix} -4 \\ 3 \\ 6 \end{pmatrix}+r\cdot \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix}=\begin{pmatrix} -4+2r \\ 3+r \\ 6-2r \end{pmatrix}$
Nun löst du insgesamt drei Gleichungen, welche du erhältst, wenn du die entsprechende Koordinate $0$ setzt.
- $6-2r=0$: Addiere $2r$ und dividiere durch $3$. Dies führt zu $r=3$ und somit zu $S_{xy}(2|6|0)$.
- $3+r$ führt durch Subtraktion von $3$ zu $r=-3$. So erhältst du $S_{xz}(-10|0|12)$.
- $-4+2r=0$: Addiere $4$ und dividiere durch $2$. So erhältst du $r=2$. Dies führt zu $S_{yz}(0|5|2)$.
Die Gerade $g$ besitzt also Spurpunkte mit jeder der Koordinatenebenen.
Kann eine Gerade eine Koordinatenebene zweimal schneiden?
Kann eine Gerade auch nur zwei Spurpunkte haben?
Betrachte nun die Gerade
$g:\vec x=\begin{pmatrix} 1 \\ 6 \\ 4 \end{pmatrix}+r\cdot \begin{pmatrix} 0 \\ -3 \\ 1 \end{pmatrix}=\begin{pmatrix} 1 \\ 6-3r \\ 4+r \end{pmatrix}$
Auch hier löst du wieder drei Gleichungen. Die Gleichung zur Berechnung des Spurpunktes mit der $y$-$z$-Koordinatenebene lautet $1=0$. Dies ist eine falsche Aussage. Das bedeutet, dass die Gerade keinen Spurpunkt, also keinen gemeinsamen Punkt, mit der $y$-$z$-Koordinatenebene besitzt. Die Gerade liegt somit parallel zu dieser Koordinatenebene.
- $6-3r=0$: Addiere $3r$ und dividiere anschließend durch $3$. Dies führt zu $r=2$ und somit zu $S_{xz}(1|0|6)$.
- $4+r=0$: Subtraktion von $4$ führt zu $r=-4$ und somit zu $S_{xy}(1|18|0)$.
Weitere Lagebeziehungen der Geraden
Einige mögliche Lagebeziehungen siehst du hier:
- Eine Ursprungsgerade ist eine Gerade, die durch den Koordinatenursprung $O(0|0|0)$ verläuft. Eine Ursprungsgerade hat den Koordinatenursprung als Spurpunkt mit jeder der Koordinatenebenen.
- Liegt eine Gerade auf einer der Koordinatenachsen, zum Beispiel der $x$-Achse, dann hat sie unendlich viele Spurpunkte mit der $x$-$y$- sowie der $x$-$z$-Koordinatenebene und einen Spurpunkt, den Koordinatenursprung, mit der $y$-$z$-Koordinatenebene.
- Liegt eine Gerade parallel zu einer der Koordinatenachsen, zum Beispiel der $y$-Achse, und zusätzlich nicht in einer der Koordinatenebenen, dann hat sie nur einen Spurpunkt mit der $x$-$z$-Koordinatenebene.
Abschließend siehst du für diesen Fall noch ein Beispiel.
Die Gerade $g$ sei wie folgt gegeben:
$g:\vec x=\begin{pmatrix} 3 \\ 2 \\ 1 \end{pmatrix}+r\cdot \begin{pmatrix} 0 \\ 5 \\ 0 \end{pmatrix}=\begin{pmatrix} 3 \\ 2+5r \\ 1 \end{pmatrix}$
Du siehst, sowohl die $x$- als auch die $z$-Koordinate eines beliebigen Punktes der Geraden sind ungleich $0$. Das bedeutet, dass die Gerade nur einen Spurpunkt mit der $x$-$z$-Koordinatenebene haben kann. Dieser ist gegeben durch $S_{xz}(3|0|1)$.
Alle Videos zum Thema
Videos zum Thema
Spurpunkte von Geraden und Schatten (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Spurpunkte von Geraden und Schatten (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter









 Spurpunkte - Billard Bandenspiel
Spurpunkte - Billard Bandenspiel
 Spurpunkte - Schatten einer Figur einzeichnen
Spurpunkte - Schatten einer Figur einzeichnen
 Berechnen von Spurpunkten
Berechnen von Spurpunkten









