Satz des Cavalieri und Eulerscher Polyedersatz
Grundfläche, Schnittfläche, Volumen
Beliebteste Videos
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Das Satz des Cavalieri
Stell dir vor, du hast einen Stapel Druckerpapier.
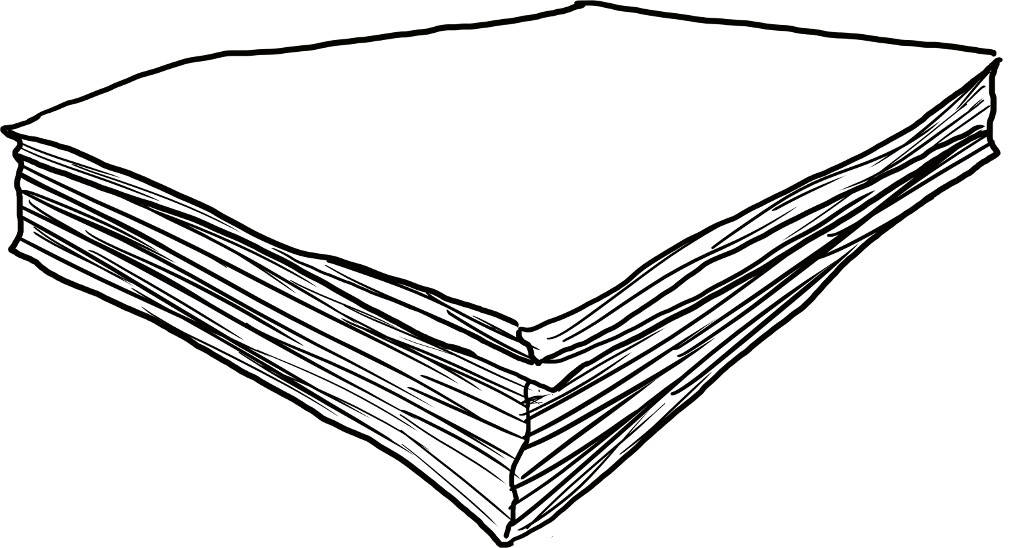
Da es sich hierbei um einen Quader handelt, kannst du dessen Volumen berechnen, indem du die Länge mit der Breite mit der Höhe des Quaders multiplizierst. Wenn du den Stapel nun ein wenig verschiebst, so dass er schräg ist: Was glaubst du, ändert sich dadurch das Volumen? Nein, ganz sicher nicht.
Das besagt der Satz des Cavalieri, oder auch das Prinzip von Cavalieri:
Zwei Körper gleicher Gesamthöhe besitzen das gleiche Volumen, wenn ihre Schnittflächen in jeder Höhe den gleichen Flächeninhalt haben.
Das Beispiel dieses blauen Quaders, zeigt das noch einmal anschaulich.
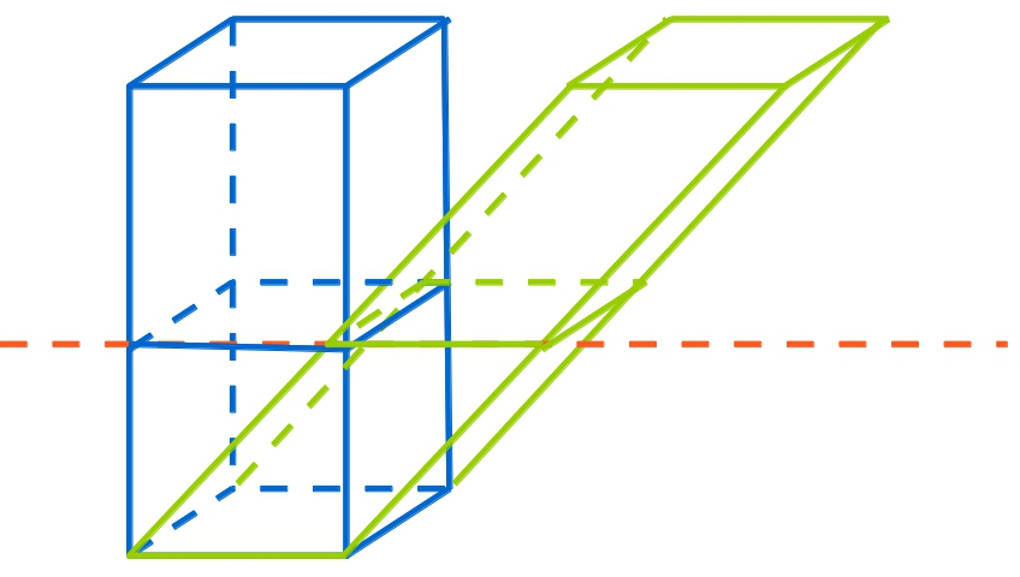
Das grüne Parallelepiped entsteht durch Verschieben aus dem blauen Quader. Dies entspricht der Situation mit dem Papierstapel. Die rote gestrichelte Linie deutet eine Schnittebene parallel zur Grundfläche des Quaders an. Die dadurch entstehenden Flächen, das blaue Rechteck und das grüne Parallelogramm, haben den gleichen Flächeninhalt. Dies gilt für jede Schnittebene. Deshalb stimmen das Volumen des Parallelepipeds und des Quaders überein.
Der Eulersche Polyedersatz
Bevor wir uns mit diesem Satz beschäftigen, wenden wir uns erst einmal dem Begriff Polyeder zu: Ein Polyeder heißt auch Vielflach. Ein Polyeder ist ein Körper, welcher ausschließlich von ebenen Flächen begrenzt wird.
Beispiele für Polyeder sind: Würfel; Quader, Pyramiden, ...
Hier siehst du einen Würfel:

Nun kannst du dir überlegen, ob Körper auch von nicht ebenen Flächen begrenzt werden können. Na klar, zum Beispiel wird eine Kugel von einer gekrümmten Fläche begrenzt, ebenso ein Kegel oder ein Zylinder. Hier siehst du zum Beispiel einen Kegel. Seine Mantelfläche ist gekrümmt.
Polyeder haben Ecken, Kanten und Flächen.
Wir schauen uns einmal ein Prisma an:
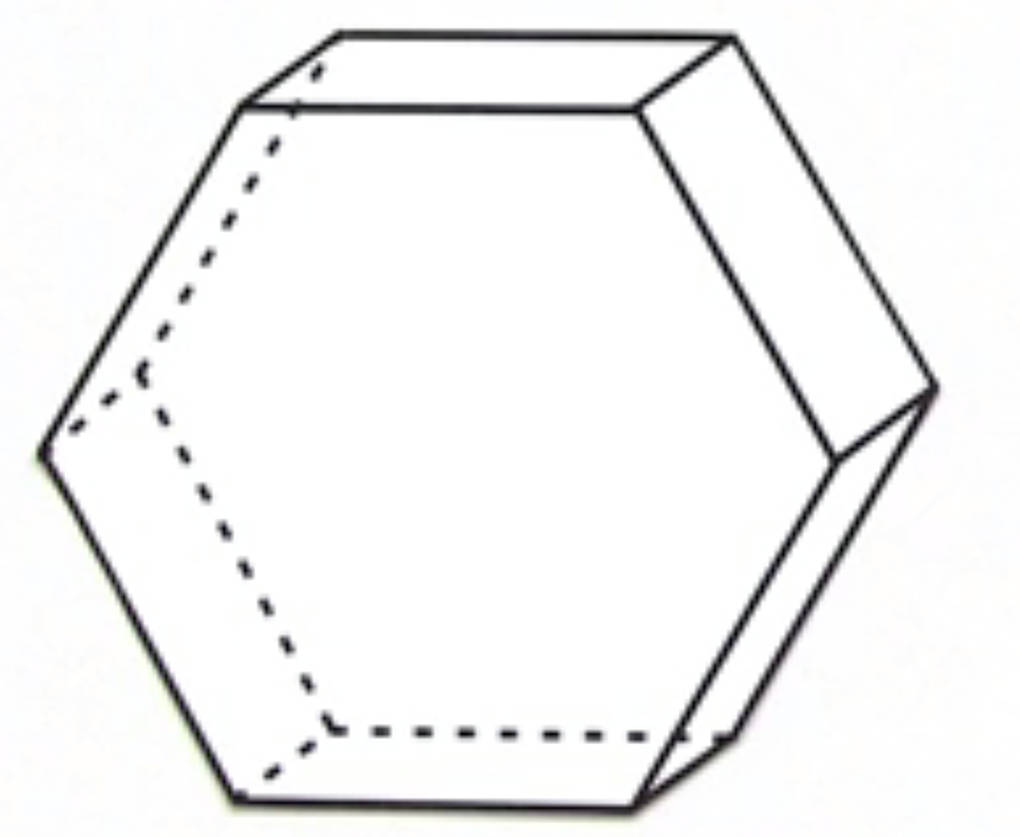
Ein Prisma setzt sich immer aus zwei beliebigen, aber deckungsgleichen (kongruenten) Vielecken als Grund- und Deckfläche zusammen. Sie sind über Kanten an den Ecken miteinander verbunden. Ganz allgemein gilt für ein Prisma mit einem $n$-Eck als Grundfläche:
Die Anzahl der Flächen beträgt $n+2$, die der Ecken $2n$ und die der Kanten $3n$.
Ein Würfel ist ein Prisma mit einem Quadrat, also einem $4$-Eck, als Grund- und Deckfläche. Der Würfel hat $2\cdot 4=8$ Ecken, $3\cdot 4=12$ Kanten und $4+2=6$ Flächen.
Nun untersuchen wir einmal, wie die jeweiligen Anzahlen zusammenhängen:
- Beim allgemeinen Prisma gilt: Die Anzahl der Kanten minus der Anzahl der Ecken plus $2$ ist gleich die Anzahl der Flächen, also $3n-2n+2=n+2$.
- Das Gleiche gilt natürlich auch für den Würfel: $12-8+2=6$, und das ist in der Tat die Anzahl der Flächen.
Dies wird im Eulerschen Polyedersatz verallgemeinert:
Seien $E$ die Anzahl der Ecken, $F$ die Anzahl der Flächen und $K$ die Anzahl der Kanten eines Polyeders, dann gilt: $E-K+F=2$.
Oder: Wie oben bereits beschrieben: $K-E+2=F$. Diese beiden Gleichungen sind äquivalent.
Alle Videos zum Thema
Videos zum Thema
Satz des Cavalieri und Eulerscher Polyedersatz (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Satz des Cavalieri und Eulerscher Polyedersatz (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter








 Schnittflächen von Prismen und Pyramiden
Schnittflächen von Prismen und Pyramiden
 Eulerscher Polyedersatz
Eulerscher Polyedersatz
 Satz des Cavalieri
Satz des Cavalieri












