Obersummen und Untersummen
Wie kannst du Inhalte von Flächen berechnen, wenn eine Grenze nicht gerade ist? Du kannst den Flächeninhalt näherungsweise mit Rechteckflächen berechnen.
Beliebteste Videos und Lerntexte
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Die Streifenmethode des Archimedes
- Eigenschaften der Unter- und Obersummen
- Berechnung einer Ober- und Untersumme
- Zusammenhang Ober- und Untersumme mit dem Hauptsatz der Differential- und Integralrechnung
Die Streifenmethode des Archimedes
Die Streifenmethode des Archimedes ist ein Verfahren, um Flächen zu berechnen, deren Grenzen nicht geradlinig sind.
Hier siehst du das Flächenstück $A$, welches von dem Funktionsgraphen der Funktion $f$ mit $f(x)=x^2$ sowie der $x$-Achse auf dem Intervall $I=[1;2]$ eingeschlossen wird. Die Grenzen $x=1$ und $x=2$ sowie $y=0$ sind geradlinig. Der Abschnitt der abgebildeten Parabel ist nicht gerade.
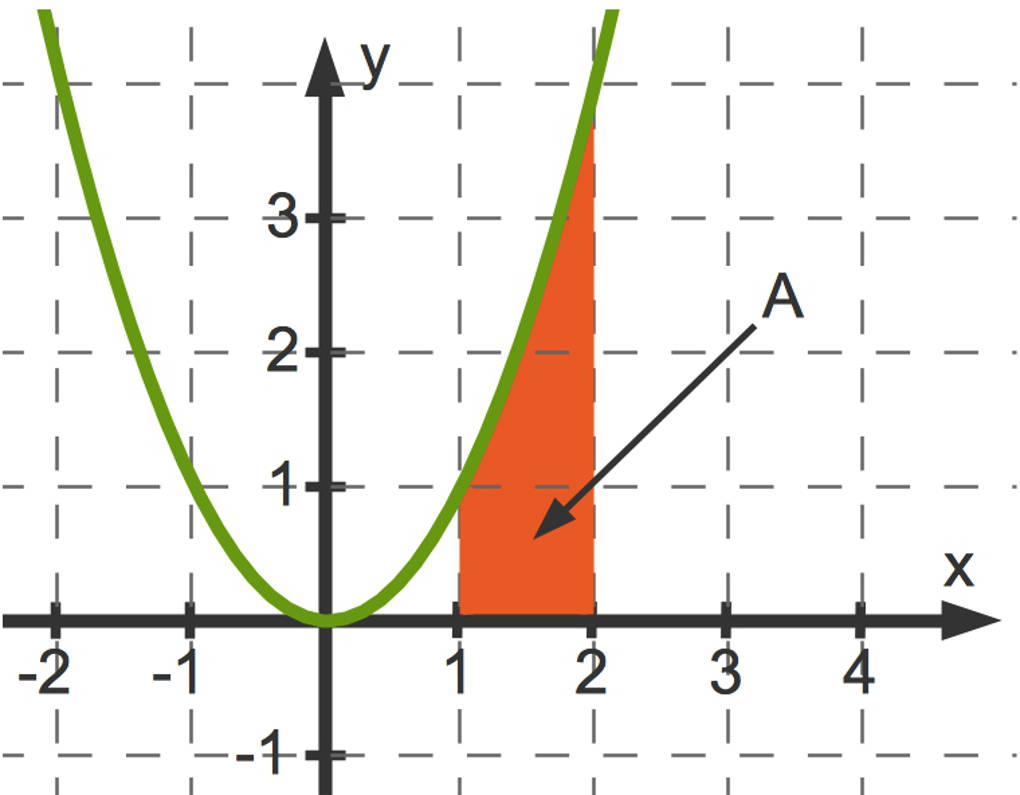
Du kannst nun das Flächenstück $A$ durch Rechtecke näherungsweise beschreiben. Dies siehst du hier anschaulich:
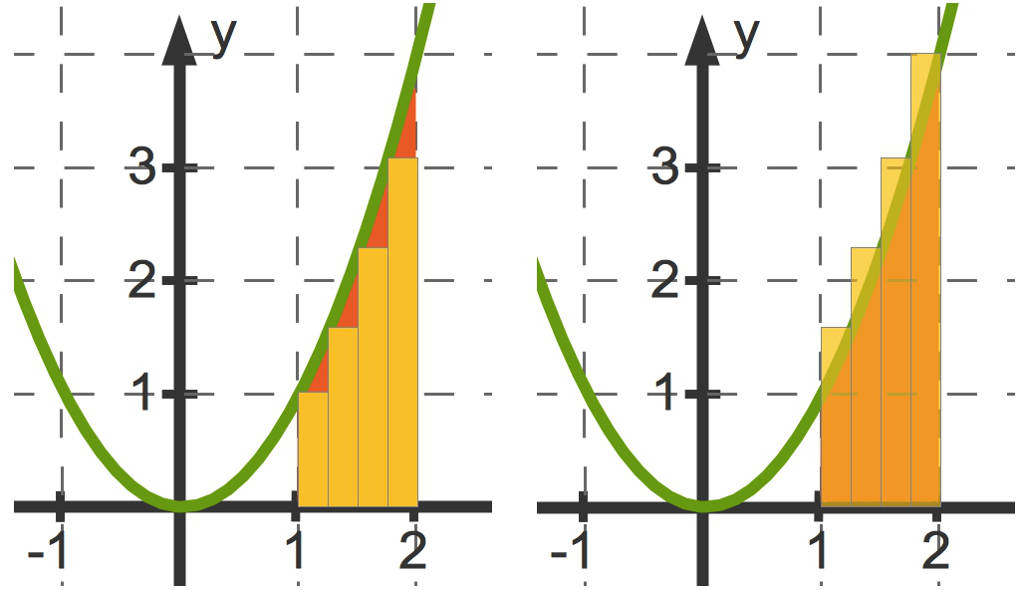
Du erkennst jeweils einen Ausschnitt des obigen Bildes, in welchem die Fläche $A$ vergrößert dargestellt ist.
Durch Zerlegung des Intervalles $[1; 2]$ in zum Beispiel vier gleich breite Streifen oder auch Rechteckflächen näherte Archimedes die tatsächliche Fläche durch zwei berechenbare Flächen an.
- Du siehst links vier Rechteckflächen, die komplett unterhalb des Funktionsgraphen liegen. Die Summe der entsprechenden Flächeninhalte ist die sogenannte Untersumme.
- Die Flächenstücke rechts liegen komplett oberhalb des Funktionsgraphen. Die resultierende Fläche als Summe der Einzelflächen wird als Obersumme bezeichnet.
Eigenschaften der Unter- und Obersummen
Es seien $U(n)$ die Untersumme und $O(n)$ die Obersumme bei Unterteilung des Intervalls in $n$ gleich große Teilintervalle.
- Wenn du das betrachtete Intervall immer feiner unterteilst, nähern die Ober- sowie die Untersumme das tatsächliche Flächenstück immer genauer an.
- Die Folge der Untersummen ist monoton wachsend, also $U(n+1)\ge U(n)$.
- Die Folge der Obersummen ist monoton fallend, also $O(n+1)\le O(n)$.
- Für jede Unterteilung des Intervalls gilt, dass die Untersumme kleiner oder gleich der Obersumme ist: $U(n)\le O(n)$.
Sei $A$ der tatsächliche Flächeninhalt, dann gilt insgesamt $U(n)\le A \le O(n)$. Darüber hinaus erhältst du: $\lim\limits_{n\to \infty} U(n)=A=\lim\limits_{n\to\infty} O(n)$
Berechnung einer Ober- und Untersumme
Wir berechnen nun die Untersumme $U(4)$ sowie die Obersumme $O(4)$ für $I=[1;2]$ und die quadratische Funktion $f$ mit $f(x)=x^2$.

Die Höhe der jeweiligen Rechtecke ist bei der Untersumme der jeweils kleinste Funktionswert auf dem entsprechenden Intervall. Dieser wird am jeweils linken Intervallrand angenommen. Bei der Obersumme ist dies der größte Funktionswert, am rechten Intervallrand. So erhältst du die folgenden Werte
$\begin{array}{rcl}U(4)&=&\frac14\cdot\left(f(1)+f(1,25)+f(1,5)+f(1,75)\right)\\ &=&\frac14\cdot\left(1^2+1,25^2+1,5^2+1,75^2\right)\\ &=&1,96875\end{array}$
und ebenso
$\begin{array}{rcl}O(4)&=&\frac14\cdot\left(f(1,25)+f(1,5)+f(1,75)+f(2)\right)\\ &=&\frac14\cdot\left(1,25^2+1,5^2+1,75^2+2^2\right)\\ &=&2,71875\end{array}$
Allgemeine Berechnung der Untersumme
Hier kannst du am Beispiel der Untersumme für die quadratische Funktion $f$ mit $f(x)=x^2$ bei Unterteilung des Intervalls $I=[0;1]$ (Intervall gewählt für einfachere Berechnung) in $n$ gleich große Teilintervalle sehen, wie der tatsächliche Flächeninhalt als Grenzwert der Untersummen berechnet werden kann.
- Berechne $U(n)=\frac1n\left(\left(\frac0n\right)^2+\left(\frac1n\right)^2+\left(\frac2n\right)^2+...+\left(\frac{n-1}n\right)^2\right)$.
- Du kannst nun den Faktor $\frac1{n^2}$ in dem Klammerterm ausklammern: $U(n)=\frac1{n^3}\left(1^2+2^2+...+(n-1)^2\right)$.
- Verwende die Summenformel $1^2+2^2+...+(n-1)^2=\frac{(n-1)\cdot n\cdot (2n-1)}{6}$.
- Schließlich erhältst du $U(n)= \frac{(n-1)\cdot n\cdot (2n-1)}{6\cdot n^3}$.
- Es ist $A=\lim\limits_{n\to\infty} U(n)=\frac26=\frac13$.
Zusammenhang Ober- und Untersumme mit dem Hauptsatz der Differential- und Integralrechnung
Diesen Flächeninhalt berechnest du mit dem Hauptsatz der Differential- und Integralrechnung als bestimmtes Integral:
$A=\int\limits_0^1~x^2~dx=\left[\frac13x^3\right]_0^1=\frac13\cdot 1^3-\frac13\cdot 0^3=\frac13$.
Du kannst nun natürlich sagen, dass die letzte Berechnung sehr viel einfacher ist. Das stimmt auch. Allerdings wird diese Regel durch die Streifenmethode nach Archimedes hergeleitet.
Abschließend kannst du noch den Flächeninhalt $A$ aus dem anfänglichen Beispiel berechnen
$A=\int\limits_1^2~x^2~dx=\left[\frac13x^3\right]_1^2=\frac13\cdot 2^3-\frac13\cdot 1^3=\frac83-\frac13=\frac73$.
Du kannst erkennen, dass $U(4)=1,96875\le\frac73\le 2,71875=O(4)$ erfüllt ist.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Obersummen und Untersummen (2 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Obersummen und Untersummen (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter







 Streifenmethode des Archimedes
Streifenmethode des Archimedes
 Was ist ein Integral?
Was ist ein Integral?












