Hauptsatz der Differential- und Integralrechnung

Inhaltsverzeichnis zum Thema

• Das unbestimmte und das bestimmte Integral
• Das unbestimmte Integral
• Das bestimmte Integral
• Die Bedeutung des bestimmten Integrals
• Der Hauptsatz der Differential- und Integralrechnung anschaulich.
• Der Hauptsatz der Differential- und Integralrechnung
• Beispiel
• Beispiele
• Beispiel 1 (Flächeninhalt)
• Beispiel 2 (Absolutbetrag)
• Beispiel 3 (Flächenbilanz)

Das unbestimmte und das bestimmte Integral

Das unbestimmte Integral

Gegeben sei $f$, eine beliebige reelle und integrierbare Funktion. Unter einer Stammfunktion einer solchen Funktion $f$ wird eine differenzierbare Funktion $F$ verstanden, deren Ableitungsfunktion $F'$ mit $f$ übereinstimmt. Ist die Funktion $f$ auf einem Intervall $I$ definiert, so muss auch $F$ auf diesem Intervall $I$ definiert und differenzierbar sein. Für alle $x$ im Intervall $I$ gilt: $F'(x)=f(x)$

Hat die Funktion $f$ eine Stammfunktion $F$, dann existieren unendlich viele Stammfunktionen von $f$. Ist $F$ eine Stammfunktion von $F$, dann ist auch für alle $c \in \mathbb{R}$ die Funktion $G$, welche durch die Summe von der Stammfunktion $F$ und $c$ definiert ist, eine Stammfunktion von $f$. Es gilt $G$ ist Stammfunktion von $f$ für beliebige reelle $c$:

$G(x)=(F(x)+c)'=F'(x)+0=f(x)$

Die Konstante $c$ wird Integrationskonstante genannt.

Die Menge aller Stammfunktionen einer Funktion $f$ ist das unbestimmtes Integral von $f$:

$\int~f(x)~dx = \{ F(x) | F'(x)=f(x) \}$

Das bestimmte Integral

Wenn zusätzlich Integrationsgrenzen $a$ und $b$ gegeben sind, dann handelt es sich nicht mehr um ein unbestimmtes Integral, sondern um ein bestimmtes Integral:

$\int\limits_a^b~f(x)~dx $

Dabei ist hier $a$ die untere und $b$ die obere Integrationsgrenze.

Die Bedeutung des bestimmten Integrals

Sei $f$ eine integrierbare Funktion, deren Graph auf dem Intervall $I=[a;b]$ komplett oberhalb der x-Achse liegt, dann lässt sich der von diesem Funktionsgraphen und der x-Achse eingeschlossene Flächeninhalt mit Hilfe des bestimmten Integrals berechnen.

Wir schauen uns dies an dem Beispiel der Funktion $f$ mit der Funktionsgleichung $f(x)=x^2$ und dem Intervall $I=[1;2]$ an.

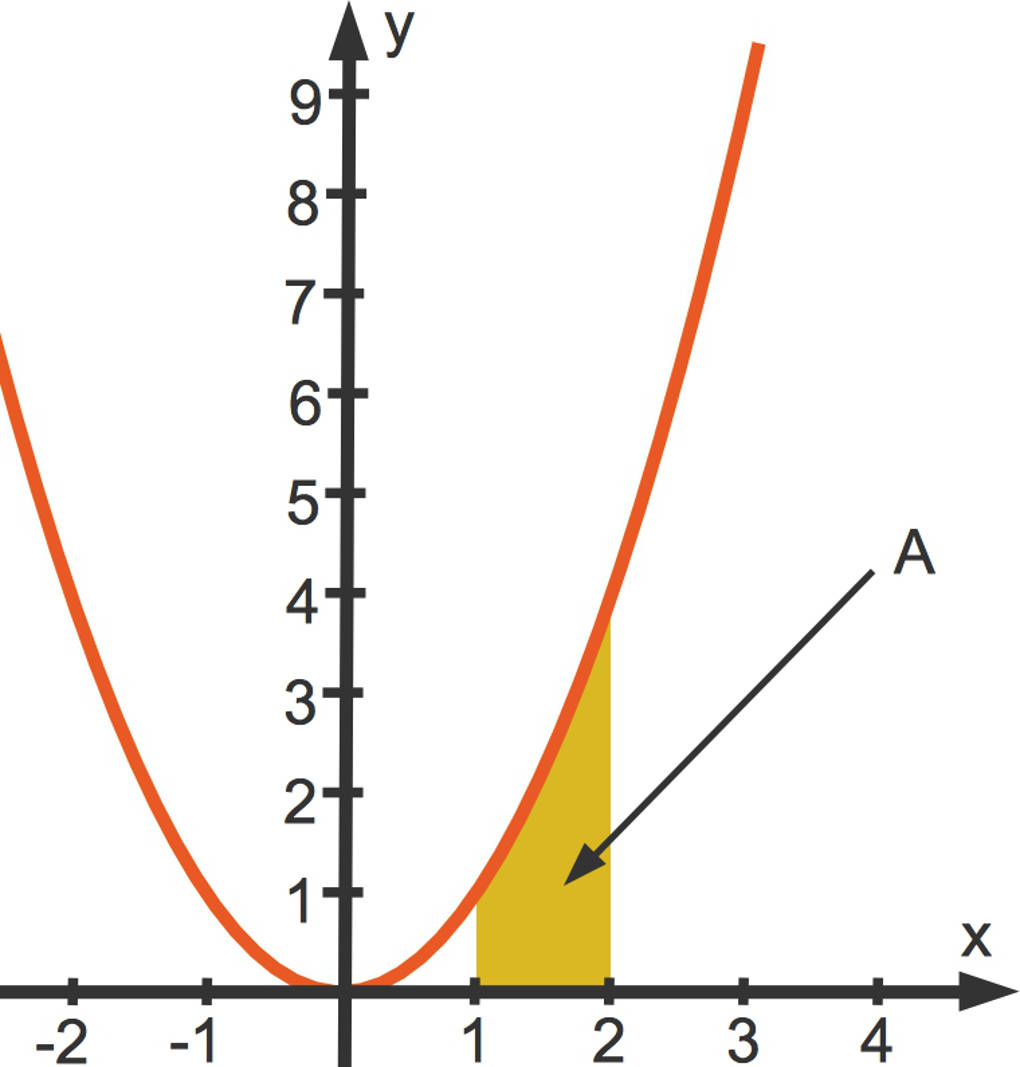
Es ist $A=\int\limits_1^2~x^2~dx$.

Nun bleibt noch die Frage, wie dieses bestimmte Integral berechnet werden soll.

Der Hauptsatz der Differential- und Integralrechnung anschaulich.

Am Beispiel der abschnittsweise konstanten Funktion $f$ kannst du nun anschaulich den Hauptsatz der Differential- und Integralrechnung sehen.

Eine abschnittsweise konstante Funktion ist eine Funktion, die aus zwei oder mehreren konstanten Funktionen zusammengesetzt ist, wobei die einzelnen Funktionen für unterschiedliche Abschnitte auf der Zahlengeraden definiert sind. An den Übergängen von einer zum anderen Teilintervall, den sogenannten Nahtstellen, sind die Funktionen nicht stetig. Solche abschnittsweise definierten Funktion $f$ sind nur stückweise stetig. Eine Stammfunktion existiert nur, wenn die Funktion $f$ den Zwischenwertsatz erfüllt. Dies ist bei abschnittsweisen konstanten Funktionen erfüllt.

Der Graph der Funktionswerte $f(x)$ ist im linken Bild blau darstellt. Die verschiedenen Farben stellen die unterschiedlichen Flächen der Funktionsabschnitten und der x-Achse dar. Auf dem rechten Bild wurde der Graph, einer von $f$ zugehörige Flächeninhaltsfunktion $F$, dargestellt (schwarz). Die Funktion beschreibt den Flächeninhalt des Graphen der Funktion $f$, der von der x-Achse und den Intervallgrenzen eingeschlossen wird.

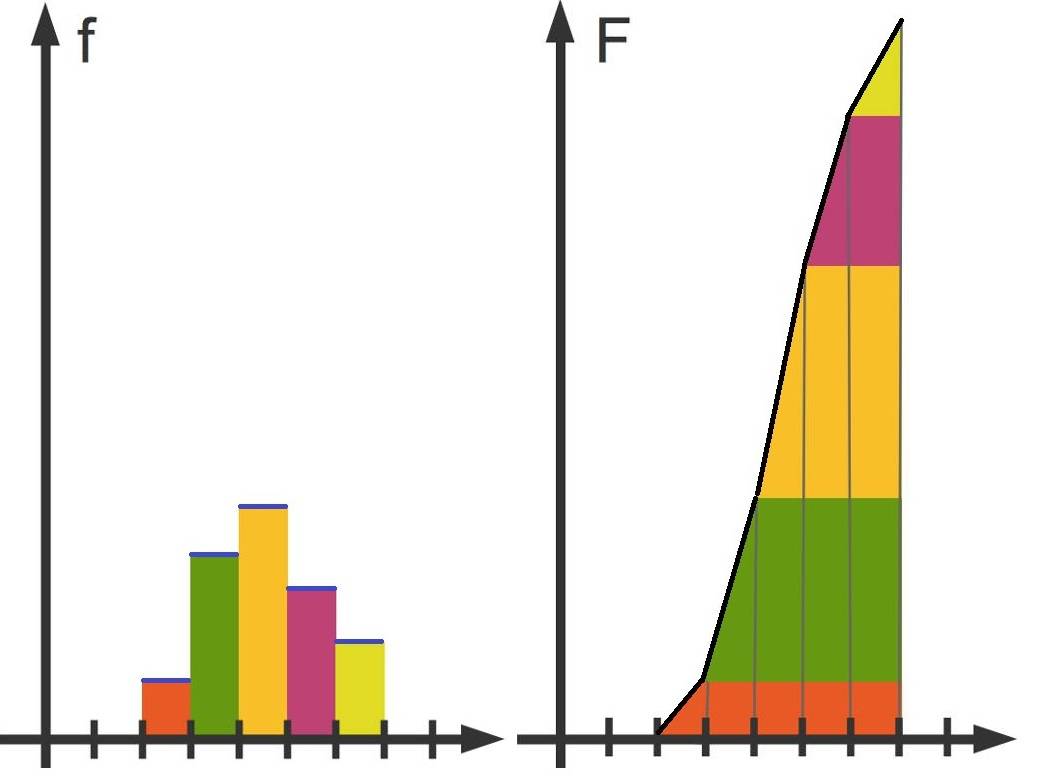
Die y-Achse ist mit $F$ beschriftet. Dies steht für den Flächeninhalt der Funktion $f$. Der Funktionswert der Stammfunktion an einer bestimmten Stelle ist der Inhalt der gesamt eingeschlossenen Fläche bis zu dieser Stelle. Du kannst an diesem Bild erkennen, dass „immer mehr Fläche dazu kommt“. Da für beliebige Werte von $x$ gilt, dass $F'(x)=f(x)$ ist $F$ eine Stammfunktion von $f$.

Zur Bestimmung der einzelnen Flächeninhalte schau dir einmal den ersten Funktionsabschnitt mit dem zugehörigen roten Rechteck, ganz links in der linken Darstellung, an. Der Flächeninhalt dieses Rechtecks (hellblau schraffiert) ist gerade der Funktionswert von $f$ multipliziert mit der Länge des Intervalls. So kommst du zu dem zugehörigen Flächeninhalt.

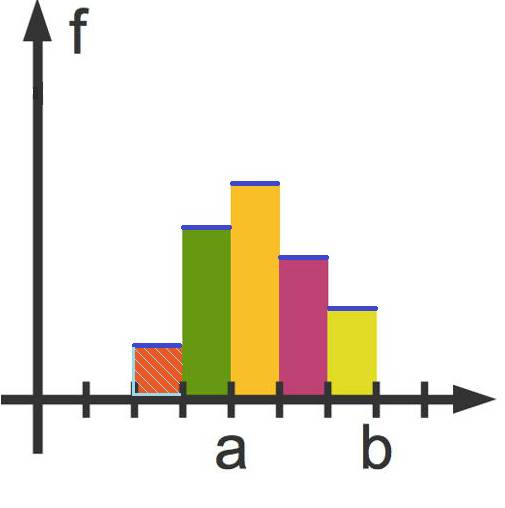
Nun schauen wir uns einmal an, welcher Flächeninhalt von dem Graphen der Funktion und der x-Achse innerhalb eines bestimmten Intervalls $I=[a;b]$ eingeschlossen wird:

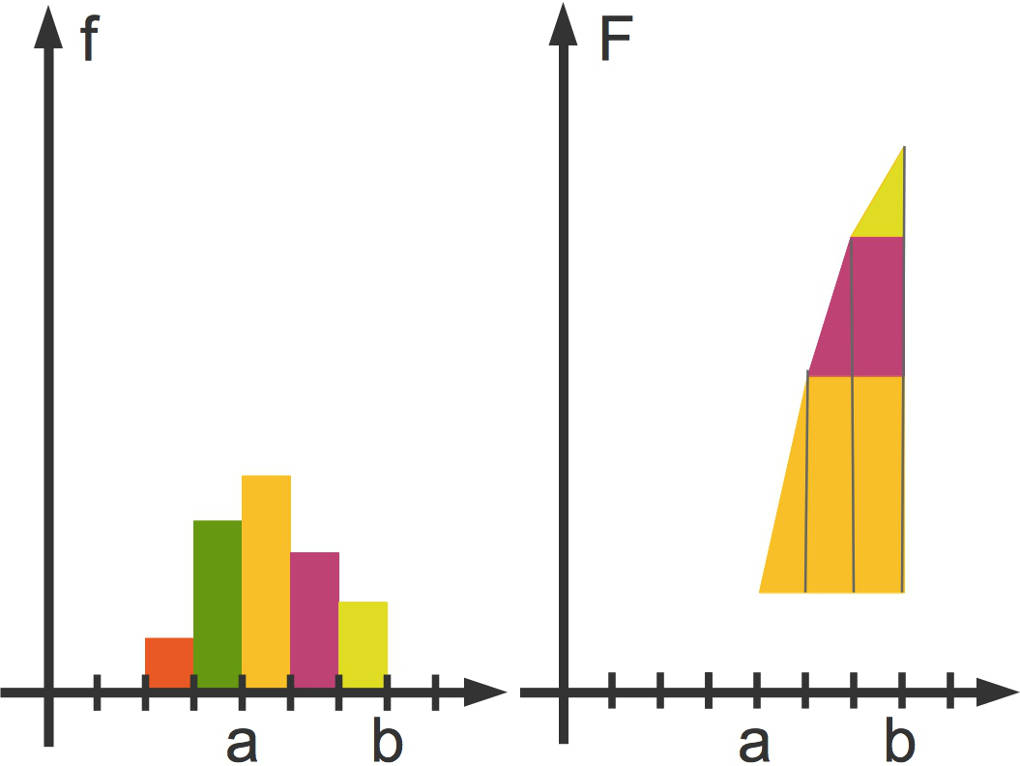
Das Intervall $I=[a;b]$ liegt zwischen dem $3.$ (gelb) und $5.$(hellgrün) Funktionsabschnitt. Der Flächeninhalten $F(a)$ der ersten beide Abschnitte (rot und grün) sollen also nicht betrachtet werden. Wobei für $F(a)$ gilt:

$F(a)=\int\limits_0^a~f(x)~dx $

Der Flächeninhalt im Intervall $I=[a;b]$ ergibt sich aus $F(a)$ subtrahiert von $F(b)$. Das bedeutet, dass der Flächeninhalt gegeben ist durch $F(b)-F(a)$.

Dies ist die Aussage des Hauptsatzes der Differential- und Integralrechnung.

Der Hauptsatz der Differential- und Integralrechnung

Den Hauptsatz der Differential- und Integralrechnung wirst du sicher sehr häufig anwenden. Mit Hilfe dieses Satzes kannst du jedes bestimmte Integral berechnen:

$\int\limits_a^b~f(x)~dx =\left[F(x)\right]_a^b=F(b)-F(a)$

Wir schauen uns diesen Satz nun etwas genauer an:

• Die Funktion $F$ ist eine Stammfunktion von $f$. Das bedeutet: $F’(x)=f(x)$
• Du musst also eine solche Stammfunktion kennen oder aber diese bestimmen.
• Nun berechnest du den Wert der Stammfunktion an der oberen Integrationsgrenze $b$ , also $F(b)$, und den an der unteren Integrationsgrenze $a$, also $F(a)$, und bildest in dieser Reihenfolge die Differenz.

Beispiel

Kommen wir wieder zu unserem Beispiel $f(x)=x^2$ zurück:

Eine Stammfunktion von $f$ ist gegeben durch $F$ mit $F(x)=\frac13x^3$. Dies kannst du durch Ableiten überprüfen.:

$F'(x)=\left(\frac13x^3\right)'=\frac13\cdot 3x^2=\frac33x^2=x^2=f(x)$

Nun können wir den Flächeninhalt berechnen:

$A=\int\limits_1^2~x^2~dx=\left[\frac13 x^3\right]_1^2=\frac13\cdot 2^3-\frac13\cdot 1^3=\frac73$

Beispiele

Im Folgenden kannst du noch an einigen Beispielen üben, wie ein bestimmtes Integral berechnet wird.

• Liegt der Funktionsgraph innerhalb des Intervalls $I=[a;b]$ komplett oberhalb der x-Achse ist das bestimmte Integral der Flächeninhalt der von dem Funktionsgraphen und der x-Achse eingeschlossenen Fläche:

$ A=\int\limits_a^b~f(x)~dx =F(b)-F(a)$

• Liegt der Funktionsgraph innerhalb des Intervalls $I=[a;b]$ komplett unterhalb der x-Achse ist das bestimmte Integral negativ. Der Absolutbetrag des bestimmten Integrals ist der Inhalt des von dem Funktionsgraphen und der x-Achse eingeschlossenen Flächenstücks.

$A=\left|\int\limits_a^b~f(x)~dx \right|=\left| F(b)-F(a)\right|$

• Hat der Funktionsgraph innerhalb des Intervalls $I=[a;b]$ eine (oder mehrere) Nullstelle(n), ist das bestimmte Integral eine Flächenbilanz.

Beispiel 1 (Flächeninhalt)

Der Funktionsgraph der kubischen Funktion $f$ mit $f(x)=x^3$ liegt innerhalb des Intervalls $I=[0;b]$ komplett oberhalb der x-Achse. Das bestimmte Integral ist der Inhalt der eingeschlossenen Fläche:

$A=\int\limits_0^2~x^3~dx=\left[\frac14x^4\right]_0^2=\frac14\cdot 2^4-\frac14\cdot 0^4=\frac{16}4=4$

Beispiel 2 (Absolutbetrag)

Der Funktionsgraph der kubischen Funktion Funktion $f$ mit $f(x)=x^3$ liegt innerhalb des Intervalls $I=[-2;0]$ vollständig unterhalb der x-Achse. Das bestimmte Integral ist folglich negativ:

$\int\limits_{-2}^0~x^3~dx=\left[\frac14x^4\right]_{-2}^0=\frac14\cdot 0^4-\frac14\cdot (-2)^4=-\frac{16}4=-4$

Der Flächeninhalt der eingeschlossenen Fläche ist dann $A=\left|\int\limits_{-2}^0~x^3~dx\right|=|-4|=4$.

Beispiel 3 (Flächenbilanz)

Der Funktionsgraph der kubischen Funktion $f$ mit $f(x)=x^3$ liegt auf dem Intervall $I=[-1;1]$ und damit sowohl oberhalb als auch unterhalb der x-Achse. Er hat eine Nullstelle bei $x_N=0$:

$\int\limits_{-1}^1~x^3~dx=\left[\frac14x^4\right]_{-1}^1=\frac14\cdot 1^4-\frac14\cdot (-1)^4=\frac14-\frac14=0$

Möchtest du bei dem obigen Beispiel einen Flächeninhalt berechnen, musst du wie folgt vorgehen:

• Ermittle zunächst die Nullstellen innerhalb des angegebenen Intervalls.
• Nun bestimmst du die Inhalte der Flächenstücke, welche unterhalb und solcher, welche oberhalb der $x$-Achse liegen.
• Schließlich addierst du die entsprechenden Flächeninhalte.