Umkehrfunktionen
Definitionsbereich, Wertebereich, Spiegelung an der Winkelhalbierenden, Umkehrfunktion bestimmen
Beliebteste Videos
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Temperatureinheiten
- Graphische Bestimmung der Umkehrfunktion
- Algebraische Bestimmung der Umkehrfunktion
Was genau ist eine Funktion?
Eine Funktion ist eine spezielle Zuordnung oder auch Abbildung. Dabei wird jedem $x$ genau ein $y$ zugeordnet. Eine Funktion $f(x)$ muss also eindeutig sein. Hier siehst du einige Beispiele für Funktionen:
- $f(x)=x$,
- $f(x)=2x^2-3x$,
- $f(x)=e^x$ heißt Exponentialfunktion mit $e\approx2,71828$, der Euler’schen Zahl.
Es gibt lineare Funktionen, quadratische Funktionen, kubische Funktionen, Exponentialfunktionen und viele andere.
Umkehrfunktionen
Temperatureinheiten
Paul möchte in den Urlaub fliegen. Geplant ist eine Reise in die USA. Paul weiß, dass Temperaturen in den USA in Grad Fahrenheit $°F$ gemessen werden. Bei ihm zu Hause werden die Temperaturen in Grad Celsius $°C$ gemessen. Die Umrechnung von $°C$ in $°F$ wird durch eine lineare Funktion dargestellt:
$f(x)=1,8\cdot x+32$.
Dabei steht das Argument $x$ der Funktion für die Angabe in $°C$ und der Funktionswert $f(x)$ für die entsprechende Angabe in $°F$.
Pauls Thermometer zeigt $30°C$ an. Wie viel Grad Fahrenheit $°F$ sind dies?

Er setzt die Angabe in $°C$ in die obige Funktionsgleichung ein und erhält $f(30)=1,8\cdot 30+32=86$. Das bedeutet, dass $30°C$ gerade $86°F$ entsprechen.
In den USA angekommen, überlegt Paul, was er anziehen soll. Er schaut auf das Thermometer: Es werden $77°F$ anzeigt. Aber wie viel Grad Celsius sind das? Paul löst eine Gleichung
$\begin{array}{rclll} 77&=&1,8\cdot x+32&|&-32\\ 45&=&1,8\cdot x&|&:1,8\\ 25&=&x\end{array}$
Nun weiß er, dass $77°F$ gerade $25°C$ entsprechen.
Je nachdem ob Paul Fahrenheit in Celsius umrechnen möchte oder andersherum, muss er einen der folgenden Wege beschreiten:
- Setzt du einen Wert für das Argument $x$ in die Funktionsgleichung ein, so erhältst du den Funktionswert. So rechnest du $°C$ in $°F$ um.
- Wenn du umgekehrt zu einem gegebenen Funktionswert das zugehörige Argument bestimmen willst, löst du die Gleichung nach $x$ auf. So rechnest du $°F$ in $°C$ um.
Der Graph der Funktion $f(x)=1,8\cdot x+32$ ist eine Gerade. Diese lässt sich in ein Koordinatensystem einzeichnen.
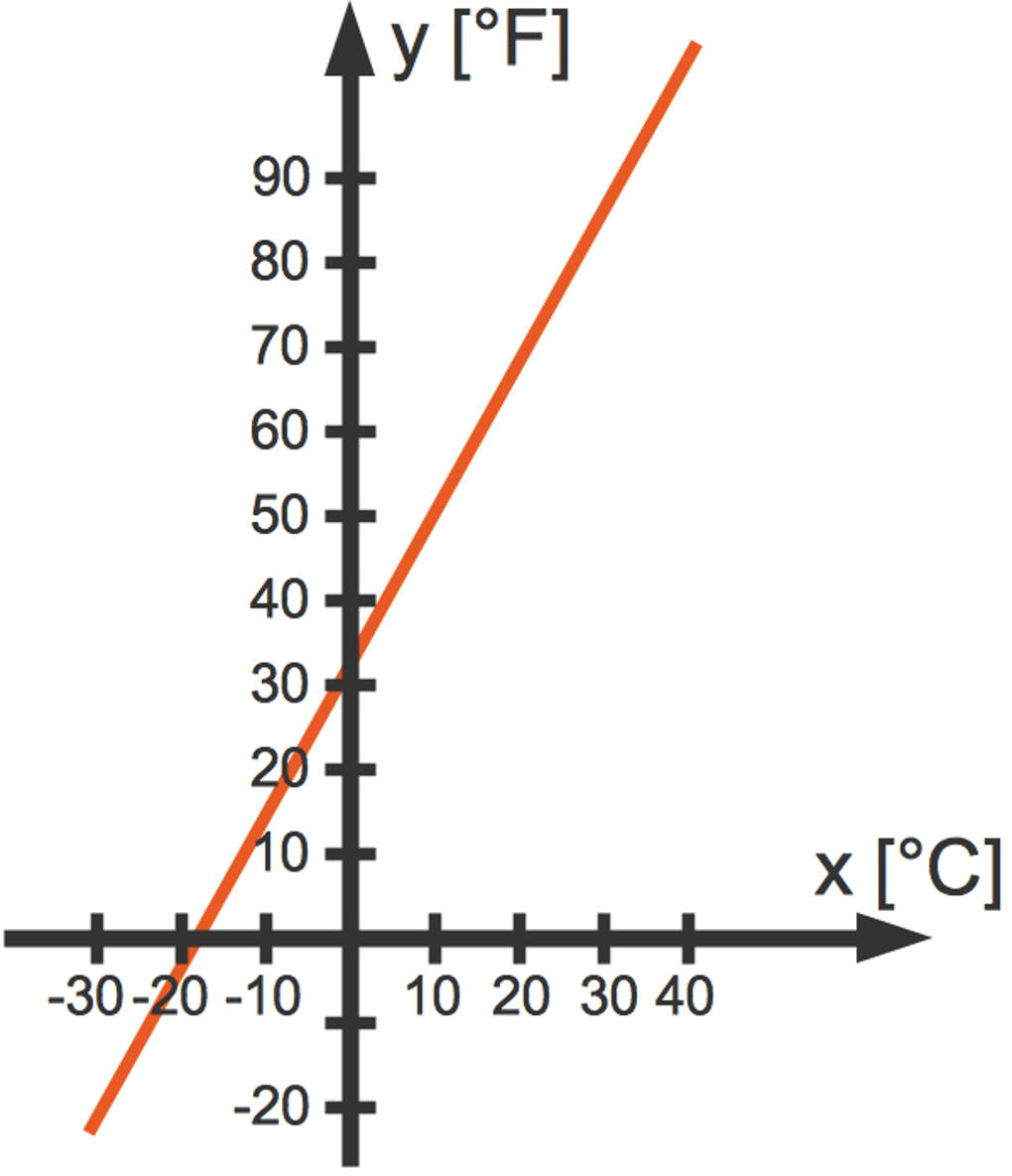
Anstatt eine komplizierte Gleichung nach $x$ aufzulösen, kannst du auch vorher die Funktion umkehren. Dies ist allerdings nur dann möglich, wenn zu jedem Funktionswert $y$ auch eindeutig ein Argument $x$ gehört. Eine solche Funktion heißt eineindeutig oder injektiv. Nicht jede Funktion ist umkehrbar, wie wir später sehen werden.
Wenn eine Funktion $y=f(x)$ umkehrbar ist, dann bezeichnet die Funktion $y=f^{-1}(x)$ die Umkehrfunktion.
Graphische Bestimmung der Umkehrfunktion
Wir wollen nun einmal Schritt für Schritt die Umkehrfunktion graphisch herleiten.
Wenn du den Graphen einer Funktion in ein Koordinatensystem gezeichnet hast, zeichnest du in das gleiche Koordinatensystem den Graphen der Identitätsfunktion $y=x$.
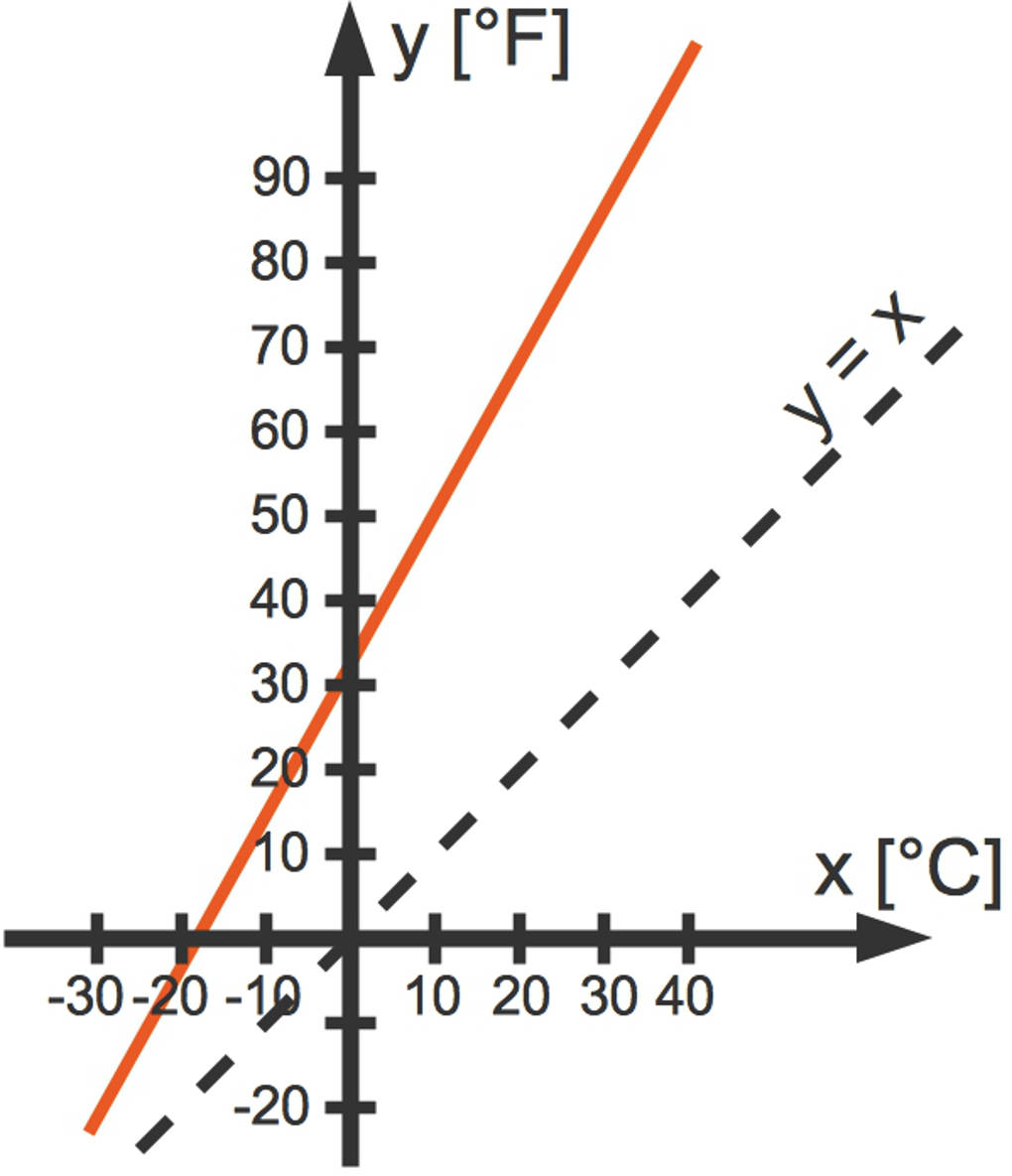
Nun spiegelst du einige Punkte des Funktionsgraphen von $f(x)$ an dieser Geraden.
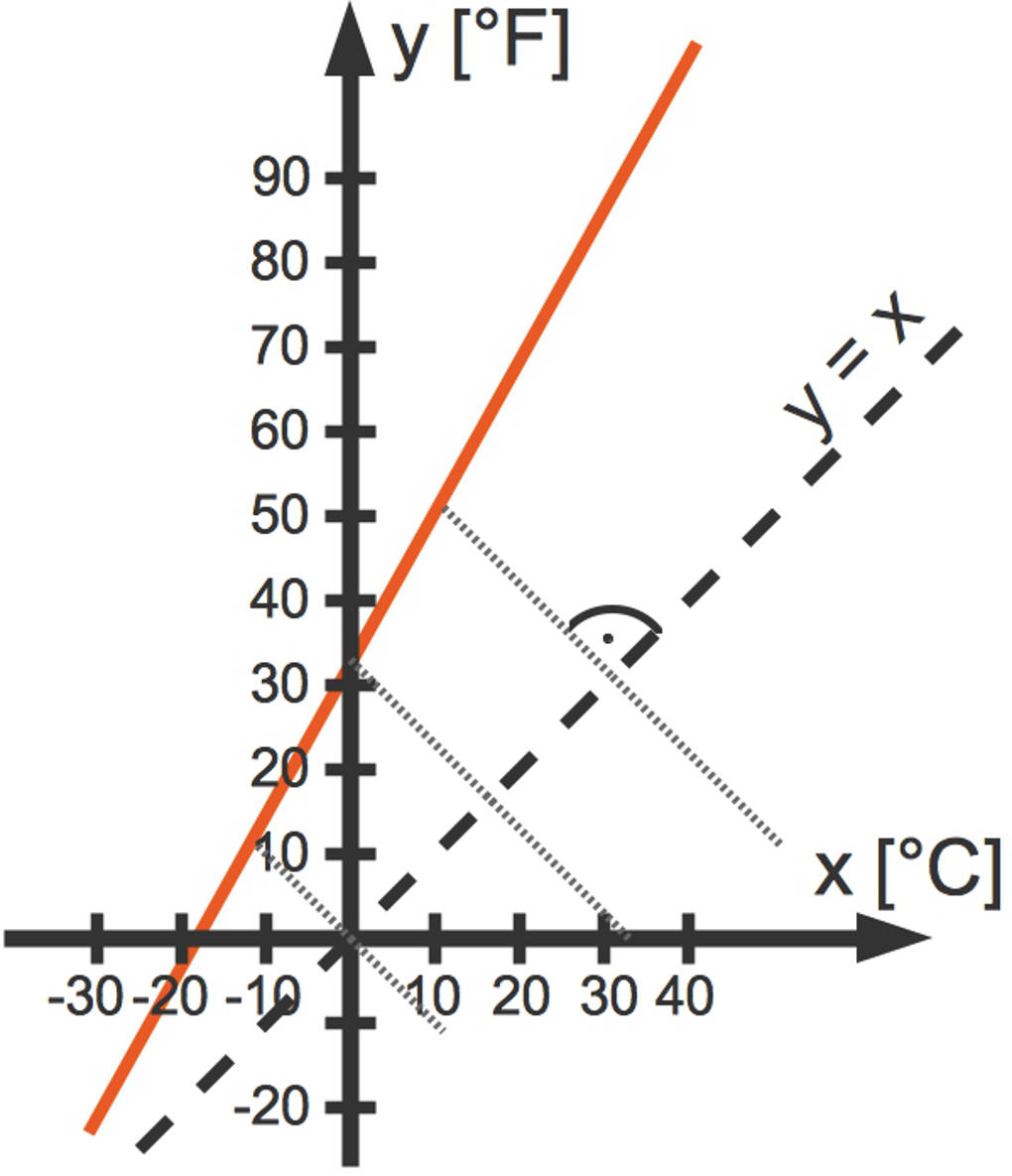
Zuletzt verbindest du die Spiegelpunkte und erhältst den Graphen der Umkehrfunktion.
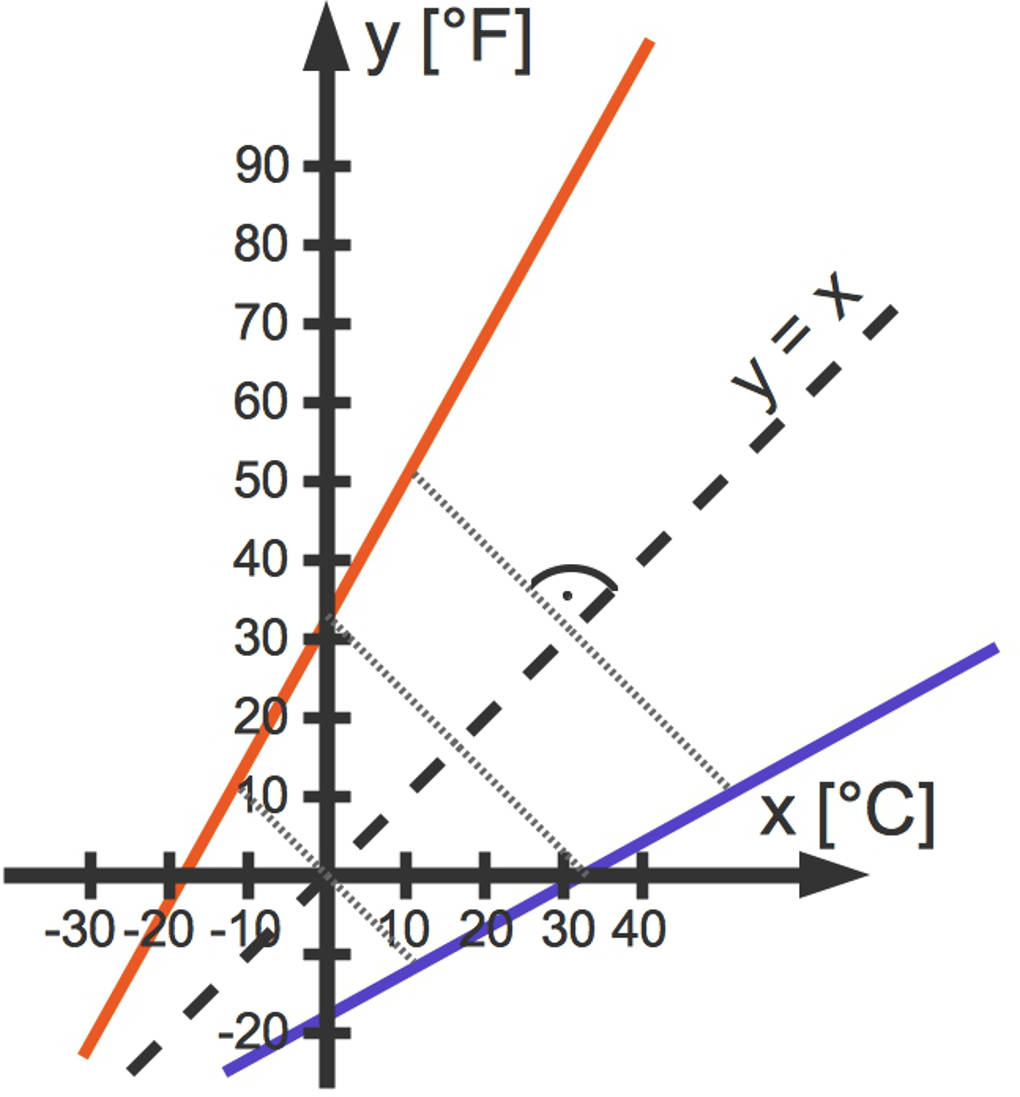
Die Nachteile dieser graphischen Bestimmung liegen auf der Hand. Zum einen kann es sehr aufwändig sein, die einzelnen Punkte zu spiegeln, und zum anderen kann die Funktionsgleichung häufig nicht exakt bestimmt werden.
Wir wollen einmal untersuchen, ob nicht auch eine rechnerische Lösung gefunden werden kann.
Algebraische Bestimmung der Umkehrfunktion
Ebenso wie Paul zu $77°F$ die zugehörige Angabe in Grad Celsius bestimmt hat, kann allgemein die Funktionsgleichung der Umkehrfunktion hergeleitet werden.
Du formst im ersten Schritt die Gleichung $y=1,8\cdot x+32$ nach $x$ um:
$\begin{array}{rclll} y&=&1,8\cdot x+32&|&-32\\ y-32&=&1,8\cdot x&|&:1,8\\ \frac{y-32}{1,8}&=&x\end{array}$
Etwas übersichtlicher können wir schreiben:
$x=\frac59\cdot y-\frac{160}9$.
Um die gewohnte Schreibweise zu benutzen, vertauschen wir die Variablen $x$ und $y$:
$y=\frac59\cdot x-\frac{160}9$.
Dann wollen wir noch kenntlich machen, dass es sich um eine Umkehrfunktion handelt. Wir ersetzen $y$ durch $f^{-1}(x)$:
$f^{-1}(x)=\frac59\cdot x-\frac{160}9$.
Lass uns doch einmal die Temperatur aus Pauls Urlaub in diese Funktionsgleichung einsetzen:
$f^{-1}(77)=\frac59\cdot 77-\frac{160}9=25$.
Ganz allgemein kann die Umkehrfunktion einer linearen Funktion $f(x)=m\cdot x+b$ so bestimmt werden:
$\begin{array}{rclll} y&=&m\cdot x+b&|&-b\\ y-b&=&m\cdot x&|&:m\\ x&=&\frac1m\cdot y-\frac bm\end{array}$
Die allgemeine Umkehrfunktion für lineare Funktionen lautet also:
$f^{-1}(x)=\frac1m\cdot x-\frac{b}m$.
Wann ist eine Funktion umkehrbar?
Eine Funktion muss eineindeutig (injektiv) sein, damit sie umkehrbar ist. Wann ist eine Funktion eineindeutig?
Jede Funktion, die entweder streng monoton wachsend oder streng monoton fallend ist, ist auch umkehrbar.
Das bedeutet, wenn eine Funktion sowohl Bereiche hat, in denen sie wächst, und solche, in denen sie fällt, ist sie nicht umkehrbar. Dies gilt zum Beispiel für die Funktion $f(x)=x^2-2$.
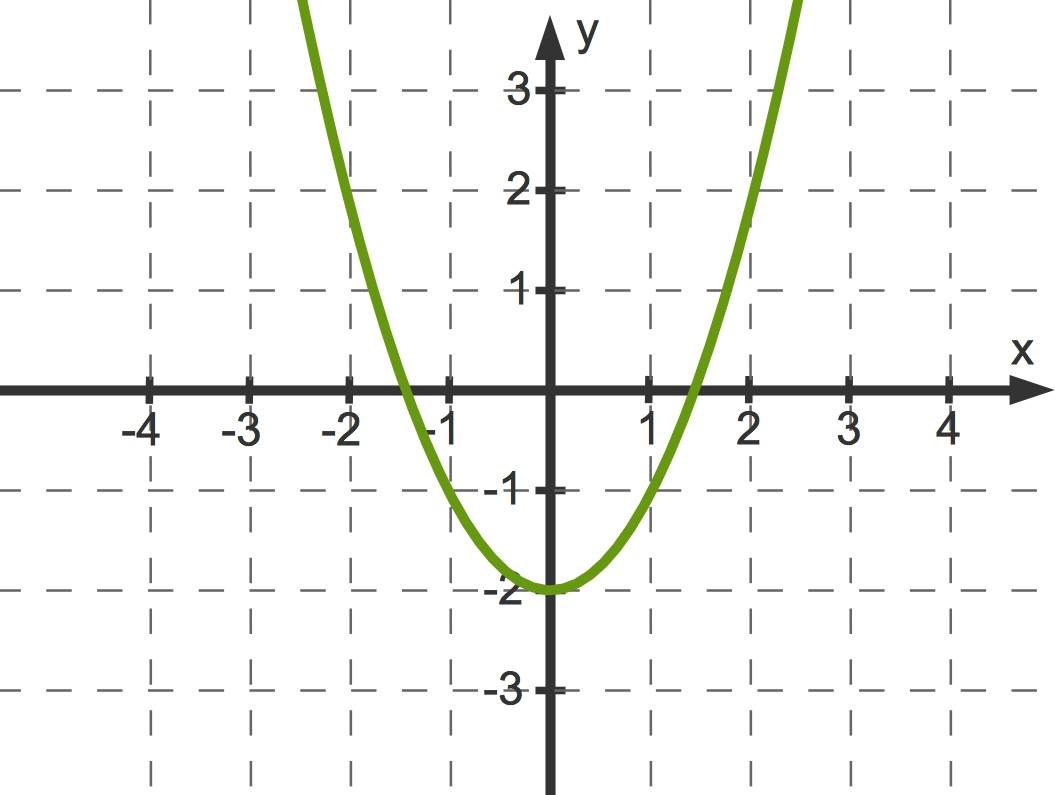
Zusammenhang zwischen Definitions- und Wertebereich
Etwas vereinfacht gesprochen, können wir sagen:
- Der Definitionsbereich der Funktion ist der Wertebereich der Umkehrfunktion.
- Der Wertebereich der Funktion ist der Definitionsbereich der Umkehrfunktion.
Die Umkehrfunktion einer Potenzfunktion
Eine Funktion $f(x)=x^n$, $n\in\mathbb{N}$, heißt Potenzfunktion. Die Umkehrbarkeit von Potenzfunktionen hängt von dem Exponenten ab. Es gibt gerade und ungerade Exponenten.
Ungerade Exponenten
Für alle ungeraden Exponenten ist die Funktion umkehrbar. Es gilt dann $\mathbb{D}_f=\mathbb{W}_f=\mathbb{R}$.
- Die Umkehrfunktion zu $f(x)=x^3$ ist die dritte Wurzel $f^{-1}(x)=\sqrt[3](x)$.
- Die Umkehrfunktion zu $f(x)=x^5$ ist die fünfte Wurzel $f^{-1}(x)=\sqrt[5](x)$.
- ...
Die Umkehrfunktion einer quadratischen Funktion
Stellvertretend für die geraden Exponenten wollen wir uns die quadratische Funktion ansehen.
Wenn man den Graphen der Funktion $f(x)=x^2$ auf den positiven x-Achsenbereich einschränkt, also $\mathbb{D}_f=\mathbb{W}_f=\mathbb{R}^+_0$, kann man diesen Graphen an der Funktionsgeraden zu $f(x)=x$ spiegeln. Der gespiegelte Funktionsgraph gehört dann zu der Wurzelfunktion $f^{-1}(x)=\sqrt x$.
Die Umkehrfunktion von quadratischen Funktionen ist die Wurzelfunktion.
Die Umkehrfunktion der natürlichen Exponentialfunktion
Die Umkehrfunktion der Exponentialfunktion $f(x)=e^x$ ist die natürliche Logarithmusfunktion $f^{-1}(x)=\ln(x)$.
Damit kannst du zu einer gegebenen Exponentialfunktion eine Umkehrfunktion herleiten. Wir schauen uns abschließend die Funktion $f(x)=e^x-3$ an.
Der Wertebereich dieser Funktion ist $\mathbb{W}_f=(-3;\infty)$, weil $e^x$ für alle reellen Zahlen größer $0$ ist. Dies ist dann auch der Definitionsbereich der Umkehrfunktion.
Wir wollen die Gleichung $y=e^x-3$ nach $x$ auflösen:
$\begin{array}{rclll} y&=&e^x-3&|&+3\\ y+3&=&e^x&|&\ln(~~~)\\ \ln(y+3)&=&x\end{array}$
Wir vertauschen nun $x$ und $y$ und ersetzen $y$ durch $f^{-1}(x)$:
$f^{-1}(x)=\ln(x+3)$.
Wie du siehst, ist der Definitionsbereich der Umkehrfunktion tatsächlich der Wertebereich der Funktion.
Alle Videos zum Thema
Videos zum Thema
Umkehrfunktionen (6 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Umkehrfunktionen (6 Arbeitsblätter)
-
 Umkehrfunktionen
PDF anzeigen
Umkehrfunktionen
PDF anzeigen -
 Was ist eine Umkehrfunktion?
PDF anzeigen
Was ist eine Umkehrfunktion?
PDF anzeigen -
 Umkehrfunktion von linearen Funktionen
PDF anzeigen
Umkehrfunktion von linearen Funktionen
PDF anzeigen -
 Umkehrfunktion von Potenzfunktionen
PDF anzeigen
Umkehrfunktion von Potenzfunktionen
PDF anzeigen -
 Wurzelfunktion als Umkehrfunktion der quadratischen Funktion
PDF anzeigen
Wurzelfunktion als Umkehrfunktion der quadratischen Funktion
PDF anzeigen -
 Logarithmusfunktion als Umkehrfunktion der Exponentialfunktion
PDF anzeigen
Logarithmusfunktion als Umkehrfunktion der Exponentialfunktion
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter


















