Grenzwerte x gegen unendlich

Inhaltsverzeichnis zum Thema

• Was ist der Grenzwert $x$ gegen unendlich?
• Grenzwerte von Funktionen durch Testeinsetzungen berechnen
• Beispiel 1
• Beispiel 2
• Grenzwerte von Funktionen durch Termvereinfachungen berechnen
• Grenzwerte von ganzrationalen Funktionen
• Ganzrationale Funktionen mit geradem Grad
• Ganzrationale Funktionen mit ungeradem Grad
• Zusammenfassung

Was ist der Grenzwert $x$ gegen unendlich?

Im Rahmen einer Kurvendiskussion musst du den Funktionsgraphen einer Funktion zeichnen. Genauer: Du zeichnest einen Ausschnitt des Funktionsgraphen. Dann bleibt immer noch die Frage, wie sich die Funktion außerhalb dieses Ausschnittes verhält. Welche Funktionswerte werden angenommen, wenn $x$ immer größer oder immer kleiner wird?

Mathematisch drückt man dies so aus:

• $\lim\limits_{x\to \infty}~f(x)=?$
• $\lim\limits_{x\to -\infty}~f(x)=?$

Es wird also nach dem Verhalten im Unendlichen gefragt, dem Grenzwert.

• Die Schreibweise „$\lim$“ steht für „Limes“, lateinisch für „Grenze“.
• Unter „$\lim$“ steht, wogegen $x$ gehen soll.

Im Folgenden schauen wir uns verschiedene Verfahren zum Bestimmen eines solchen Grenzwertes an.

Grenzwerte von Funktionen durch Testeinsetzungen berechnen

Bei der Grenzwertbestimmung durch Testeinsetzung gehst du wie folgt vor.

Du erstellst eine Wertetabelle. Dabei wählst du Werte für $x$, die immer größer (also $x\to \infty$) oder immer kleiner (also $x\to -\infty$) werden. Zu diesen Werten berechnest du die zugehörigen Funktionswerte. Das Verhalten dieser Funktionswerte zeigt dir dann an, wogegen die Funktionswerte schließlich gehen.

Beispiel 1

Dies schauen wir uns einmal an einem Beispiel an: $f(x)=\frac{x^2+1}{x^2}$.

Beachte, dass der Definitionsbereich dieser Funktion $\mathbb{D}_f=\mathbb{R}\setminus\{0\}$ ist. Das bedeutet, dass der Funktionsgraph an der Stelle $x=0$ eine Polstelle hat (oder haben kann!).

Den zugehörigen Funktionsgraphen kannst du hier sehen.

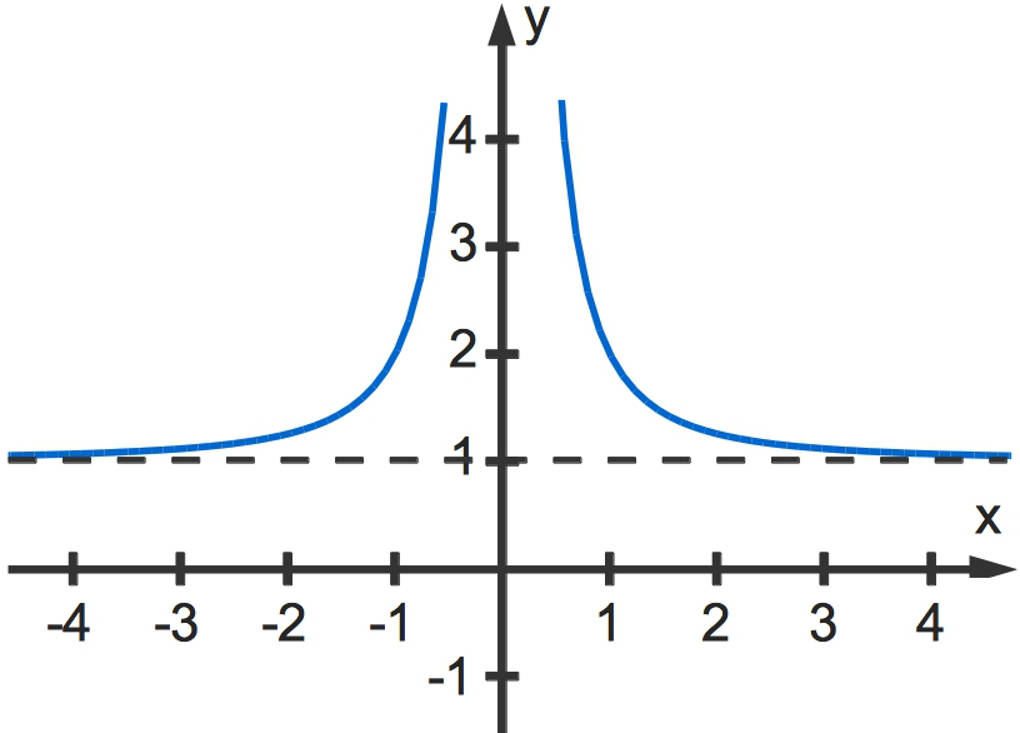
Du kannst daran auch bereits erkennen, dass sich der Funktionsgraph an eine zur $x$-Achse parallele Gerade durch $y=1$ anschmiegt.

Damit gilt:

$\lim\limits_{x\to\infty}~f(x)=1$

Ebenso kannst du den Grenzwert für $x\to-\infty$ bestimmen. Dieser ist ebenfalls $1$.

Beispiel 2

Wir schauen uns noch ein weiteres Beispiel an: $f(x)=\frac{x^2-1}{x+2}$.

Der Definitionsbereich dieser Funktion ist $\mathbb{D}_f=\mathbb{R}\setminus\{-2\}$. Hier siehst du den Teil des Funktionsgraphen für $x>-2$.

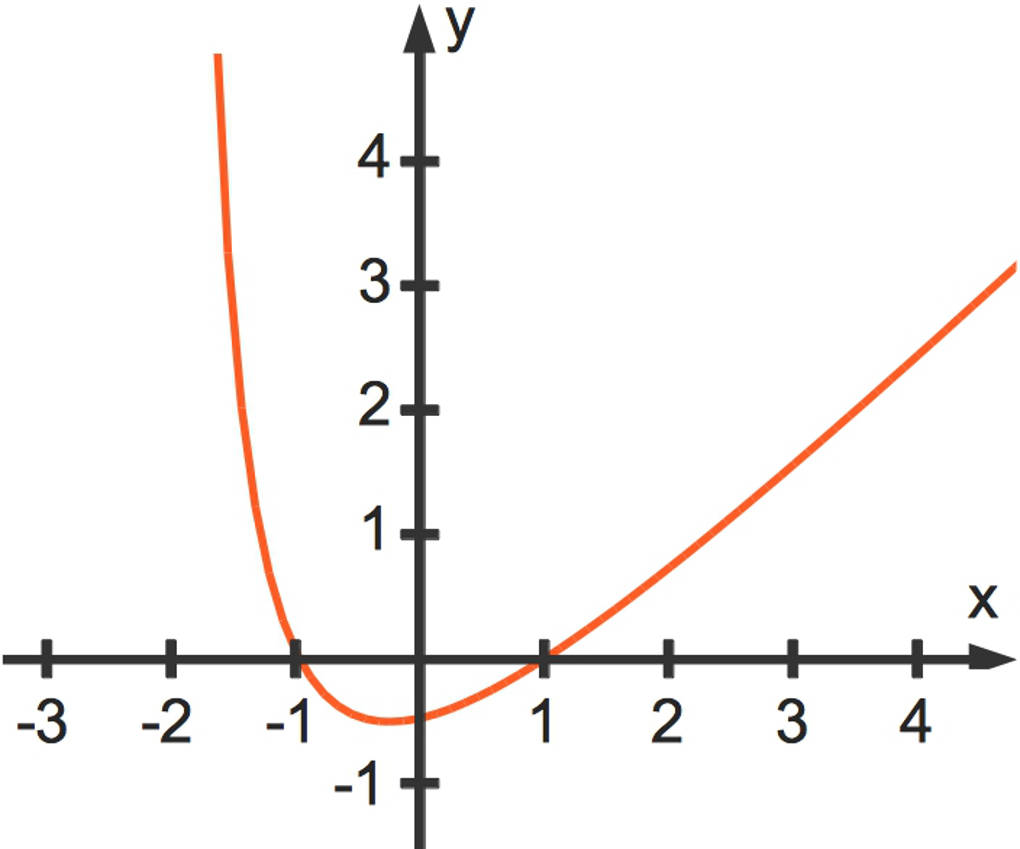
In der folgenden Wertetabelle siehst du wieder die Funktionswerte zu einigen $x$.

Du kannst sowohl an dem Funktionsgraphen als auch an der Wertetabelle erkennen, dass die Funktionswerte für immer größer werdende $x$ auch immer größer werden. Es gilt also:

$\lim\limits_{x\to\infty}~f(x)=$„$\infty$“

In diesem Fall liegt ein uneigentlicher Grenzwert, also keine endliche Zahl, vor. Deswegen schreibt man dies oft in Anführungszeichen.

Grenzwerte von Funktionen durch Termvereinfachungen berechnen

Das Verfahren durch Testeinsetzung ist streng genommen nicht korrekt. Warum? Es könnte zufällig so sein, dass du eine Folge von $x$ gefunden hast, welche gegen unendlich geht, für die der entsprechende Grenzwert für die Funktion herauskommt. Bei einer anderen Folge könnte auch der Grenzwert ein anderer sein. Dies ist allerdings bei den betrachteten Funktionen nicht der Fall.

Etwas „ mathematischer“ ist das Verfahren der Termvereinfachung oder auch Termumformung.

Hierfür schauen wir uns noch einmal das erste Beispiel an: $f(x)=\frac{x^2+1}{x^2}$.

Der Grenzwert ist bereits bekannt. Dieser ist $1$.

Der Funktionsterm wird nun umgeformt. Du kannst jeden Summanden im Zähler durch den Nenner dividieren und erhältst dann:

$f(x)=\frac{x^2+1}{x^2}=1+\frac1{x^2}$

Nun kannst du dir jeden einzelnen Summanden anschauen. Du verwendest hierfür die Grenzwertsätze.

Der Grenzwert der Summe zweier Funktionen ist gleich der Summe der Grenzwerte der einzelnen Summanden. Dies gilt ebenso für Differenzen:

$\lim\limits_{x\to\infty}(f(x)\pm g(x))=\lim\limits_{x\to\infty}f(x)\pm\lim\limits_{x\to\infty}g(x)$

Also gilt:

$\lim\limits_{x\to\infty}f(x)=\lim\limits_{x\to\infty}\left(1+\frac1{x^2}\right)=\lim\limits_{x\to\infty}1+\lim\limits_{x\to\infty}\frac1{x^2}$

Der linke Grenzwert ist $1$, da eine konstante Funktion betrachtet wird, und der rechte ist $0$, also folgt insgesamt:

$\lim\limits_{x\to\infty}f(x)=\lim\limits_{x\to\infty}1+\lim\limits_{x\to\infty}\frac1{x^2}=1+0=1$

Grenzwerte von ganzrationalen Funktionen

Eine ganzrationale Funktion sieht wie folgt aus:

$f(x)=a_n\cdot x^n+a_{n+1}\cdot x^{n-1}+...+a_2\cdot x^2+a_1\cdot x+a_0$

Dabei ist $n$ der Grad, die höchste Potenz, und $a_n$ der zugehörige Koeffizient der ganzrationalen Funktion.

Das Grenzwertverhalten ganzrationaler Funktionen hängt

• zum einen davon ab, ob der Grad $n$ gerade oder ungerade ist und
• zum anderen davon, ob der Koeffizient $a_n$ vor dem $x$ mit der höchsten Potenz positiv oder negativ ist.

Dies schauen wir uns jeweils an einem Beispiel an.

Ganzrationale Funktionen mit geradem Grad

Es sollen die Grenzwerte für $x$ gegen plus und minus unendlich der Funktion $f(x)=x^2$ bestimmt werden. Der Funktionsgraph ist eine nach oben geöffnete Parabel.

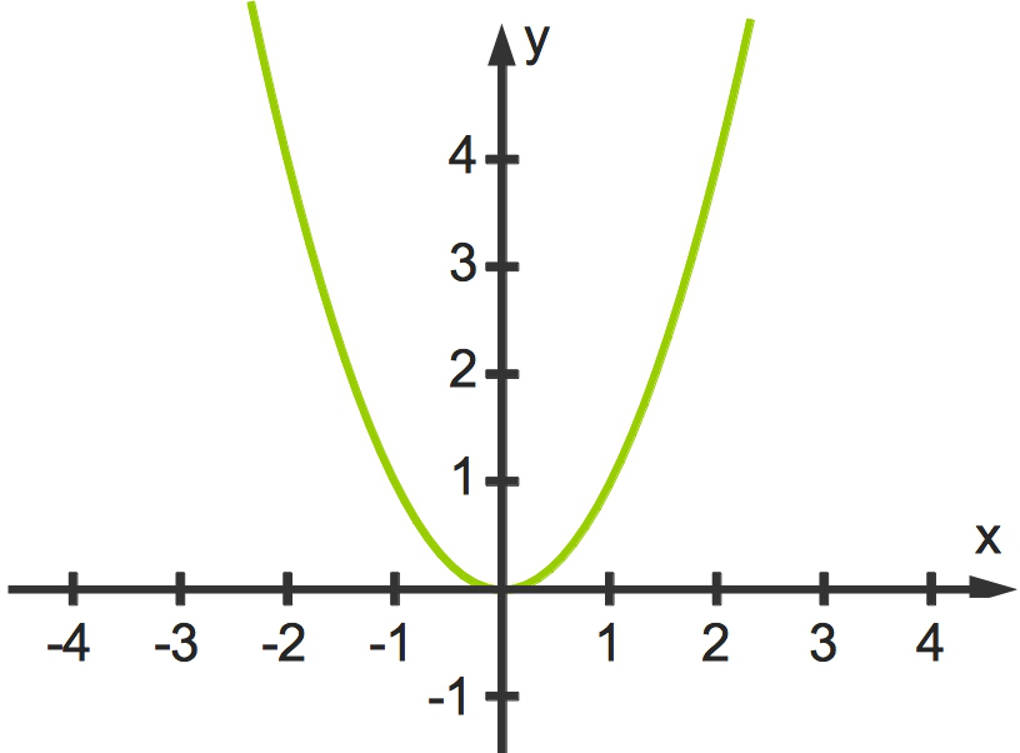
Du kannst hier erkennen, dass sowohl für immer größer als auch für immer kleiner werdende $x$ die Funktionswerte immer größer werden, also gegen unendlich gehen. Dies kannst du natürlich durch Testeinsetzung überprüfen. Es gilt also

$\lim\limits_{x\to\infty}~f(x)=\lim\limits_{x\to-\infty}~f(x)=$„$\infty$“.

Wenn du statt $f(x)=x^2$ die Funktion $g(x)=-x^2$ betrachtest, erhältst du eine an der $x$-Achse gespiegelte, also nach unten geöffnete, Parabel. Damit gilt

$\lim\limits_{x\to\infty}~g(x)=\lim\limits_{x\to-\infty}~g(x)=$„$-\infty$“.

Ganzrationale Funktionen mit ungeradem Grad

Hierfür schauen wir uns die Funktion $f(x)=x^3$ mit dem dazugehörigen Funktionsgraphen an.

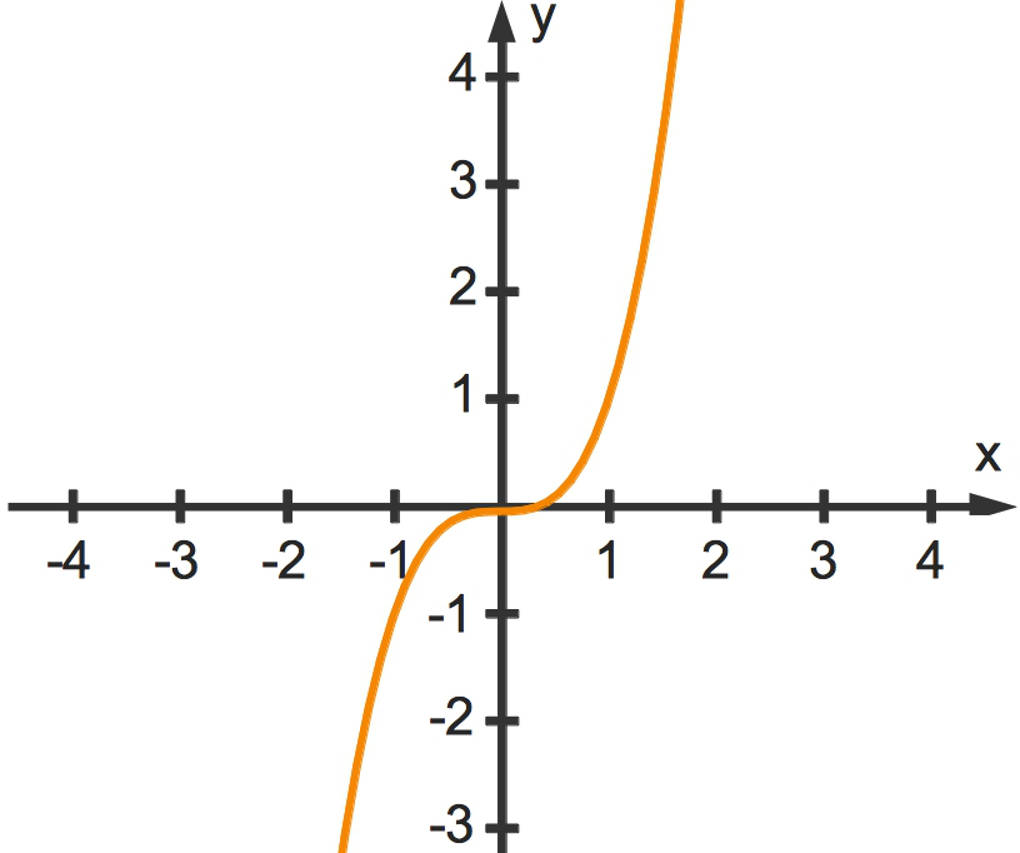
Hier kannst du die folgenden Grenzwerte erkennen:

$\lim\limits_{x\to\infty}~f(x)=$„$\infty$“ und

$\lim\limits_{x\to-\infty}~f(x)=$„$-\infty$“.

Auch hier führt die Spiegelung an der $x$-Achse zu einer Vorzeichenveränderung bei den Grenzwerten. Für $g(x)=-x^3$ gilt

$\lim\limits_{x\to\infty}~g(x)=$„$-\infty$“ sowie

$\lim\limits_{x\to-\infty}~g(x)=$„$\infty$“.

Zusammenfassung

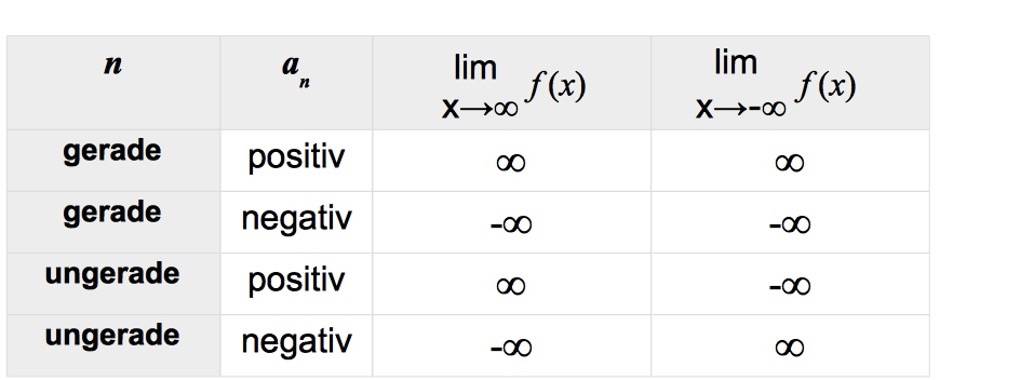
Du siehst, je nach Grad $n$, gerade oder ungerade, und entsprechendem Koeffizienten $a_n$, positiv oder negativ, kannst du die Grenzwerte einer ganzrationalen Funktion

$f(x)=a_n\cdot x^n+a_{n+1}\cdot x^{n-1}+...+a_2\cdot x^2+a_1\cdot x+a_0$

direkt angeben. Die folgende Tabelle soll dir hierfür einen Überblick geben.