Vierfeldertafel
Einfach lernen mit Videos, Übungen, Aufgaben & Arbeitsblättern
Beliebteste Videos
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was ist eine Vierfeldertafel?
Die Vierfeldertafel ist eine Tabelle. Diese verwendest du, um absolute oder relative Häufigkeiten, also Verteilungen, oder auch Wahrscheinlichkeiten zu erfassen.
Dabei werden zwei Merkmale berücksichtigt, zum Beispiel $A$ und $B$.
- Es gibt zwei Spalten für die Merkmalsausprägungen von $A$ ($A$ und $\bar{A}$)
- sowie zwei Zeilen für die Merkmalsausprägungen von $B$ ($B$ und $\bar{B}$).
- Somit gibt es im Inneren der Tabelle vier Felder.
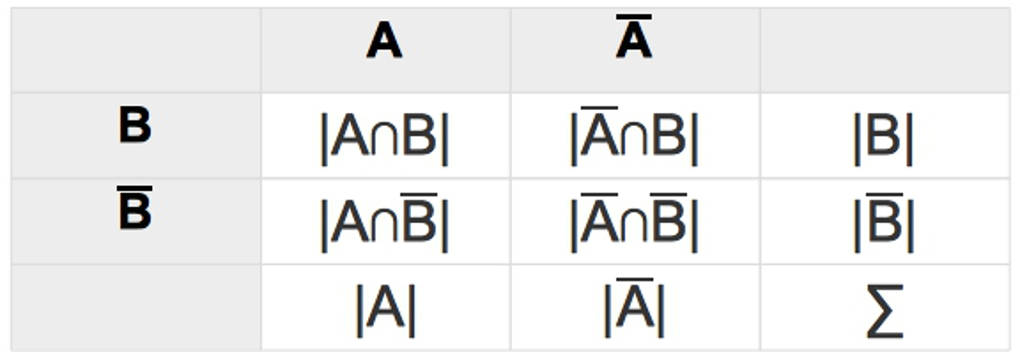
In dieser Vierfeldertafel sind die absoluten Häufigkeiten eingetragen:
- Zum Beispiel gibt $|A\cap B|$ die absolute Häufigkeit für das gemeinsame Eintreten von Merkmal $A$ und $B$ an. Dabei steht $\cap$ für den Schnitt.
- $\Sigma$ gibt die Gesamtanzahl an.
- Jede absolute Häufigkeit in der untersten Zeile ist die Summe der beiden darüber stehenden absoluten Häufigkeiten. So ist zum Beispiel $|A|=|A\cap B|+|A\cap \bar{B}|$.
- Jede absolute Häufigkeit in der letzten Spalte ist die Summe der beiden absoluten Häufigkeiten links daneben: $|B|=|A\cap B|+|\bar{A}\cap B|$.
- Die letzte Zeile und die letzte Spalte müssen jeweils in der Summe $|A|+|\bar{A}|=|B|+|\bar{B}|=\Sigma$ ergeben.
Mit Hilfe einer Vierfeldertafel kannst du relative Häufigkeiten oder Wahrscheinlichkeiten sowie bedingte Wahrscheinlichkeiten berechnen.
Die Vierfeldertafel kann auch mit Wahrscheinlichkeiten angegeben sein:
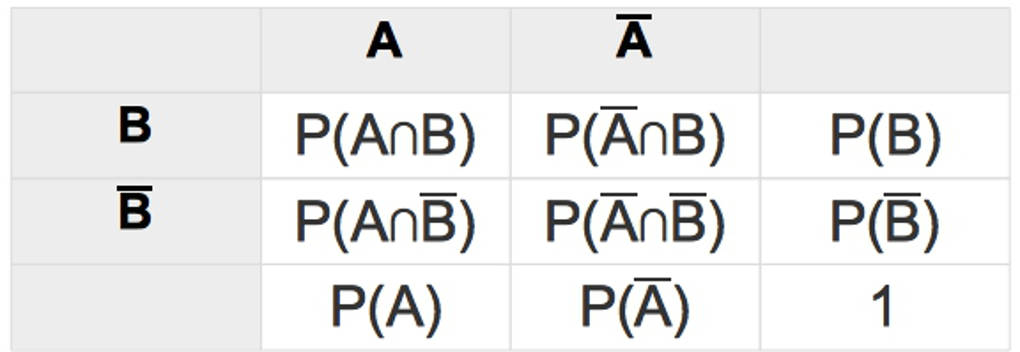
Du siehst, dass unten rechts die $1$ steht. Diese Wahrscheinlichkeit ergibt sich, wenn du entweder $P(A)+P(\bar{A})$ oder $P(B)+P(\bar{B})$ berechnest.
Beispiel
Schauen wir uns doch einmal ein Beispiel an. Es wird eine Untersuchung zum Frühstücksverhalten in Abhängigkeit vom Geschlecht untersucht.
- $F$ steht für „... frühstückt mindestens fünfmal pro Woche.“
- $\bar{F}$ steht für „... frühstückt höchstens viermal pro Woche.“
- $W$ steht für „Frau“ und
- $\bar{W}$ für „Mann“.
Es werden insgesamt $500$ Personen ($\Sigma$) befragt.
- Von diesen sind $270$ Frauen ($|W|$).
- Von den Frauen frühstücken $180$ mindestens fünfmal pro Woche ($|F\cap W|$) und
- von den Männern frühstücken $160$ höchstens viermal pro Woche ($|\bar{F}\cap \bar{W}|$).
Nun kannst du mit diesen Werte eine Vierfeldertafel erstellen:
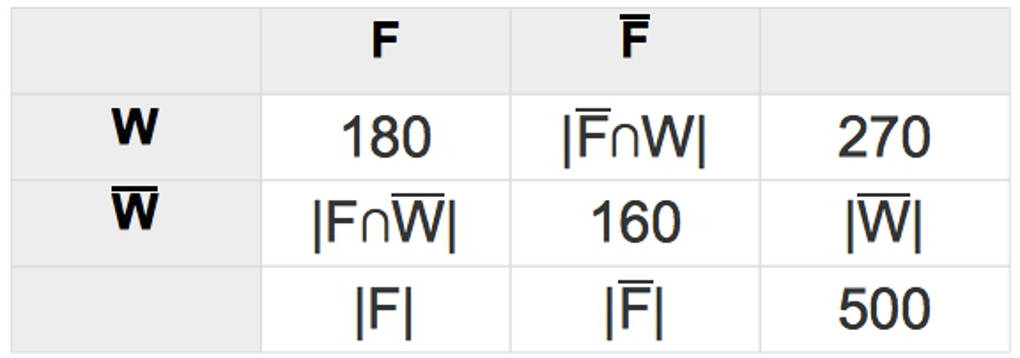
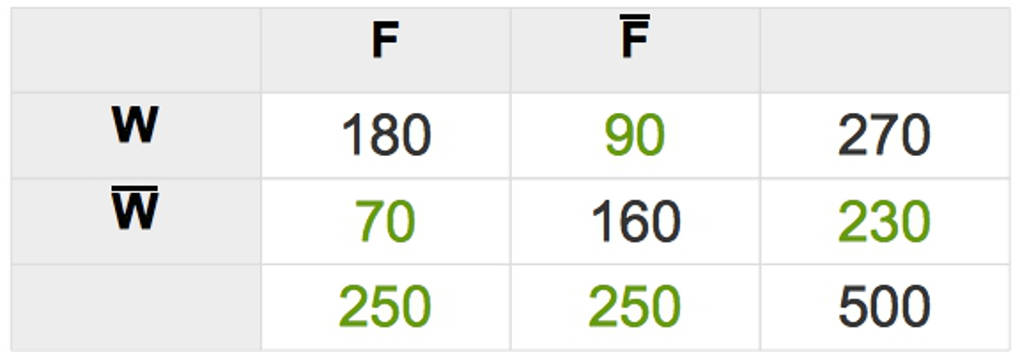
Allerdings fehlen noch einige Werte. Diese kannst du ermitteln, wenn du bedenkst, dass zum Beispiel $|F\cap W|+|\bar{F}\cap W|=270$ ist. Ebenso kannst du die übrigen noch freien Felder ausfüllen.
Auf diese Weise kannst du die Vierfeldertafel vervollständigen.
Wahrscheinlichkeiten mit Hilfe einer Vierfeldertafel berechnen
Randwahrscheinlichkeiten

Die Randwahrscheinlichkeiten sind die Wahrscheinlichkeiten für das Eintreten eines Merkmals. Diese sind:
- $P(A)=\frac{|A|}{\Sigma}$,
- $P(\bar{A})=\frac{|\bar{A}|}{\Sigma}$,
- $P(B)=\frac{|B|}{\Sigma}$ und
- $P(\bar{B})=\frac{|\bar{B}|}{\Sigma}$.

Am Beispiel des Frühstücksverhaltens können die folgenden Randwahrscheinlichkeiten oder auch relativen Randhäufigkeiten berechnet werden:
- $P(W)=\frac{270}{500}=0,54$,
- $P(\bar{W})=\frac{230}{500}=0,46$,
- $P(F)=\frac{250}{500}=0,5$ und
- $P(\bar{F})=\frac{250}{500}=0,5$.
Wenn du die Randwahrscheinlichkeiten oder relativen Randhäufigkeiten
- in der rechten Spalte ($0,54+0,46$) oder
- der unteren Zeile ($0,5+0,5$) addierst,
kommt immer $1$ heraus.
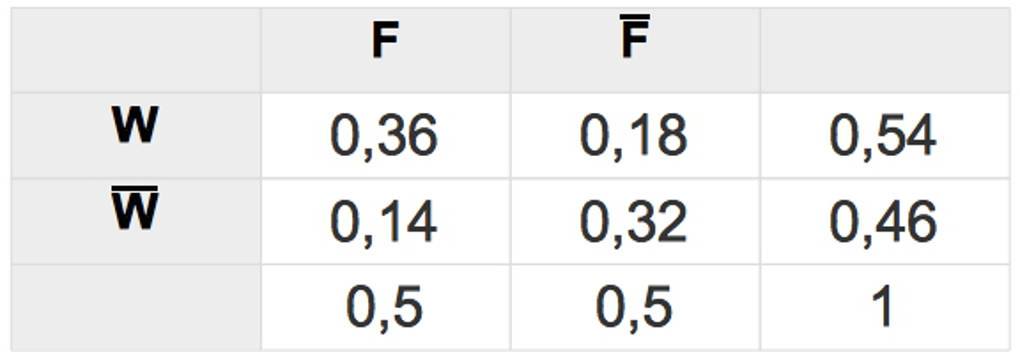
In dieser Vierfeldertafel sind auch noch die übrigen Wahrscheinlichkeiten $P(F\cap W)=0,36$, $P(\bar F\cap W)=0,18$, $P(F\cap \bar W)=0,14$ sowie $P(\bar F\cap \bar W)=0,32$ eingetragen.
Bedingte Wahrscheinlichkeiten
Eine bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit für das Eintreten eines Ereignisses unter der Bedingung, dass ein anderes Ereignis bereits eingetreten ist.
Bedingte Wahrscheinlichkeiten können mit Hilfe einer Vierfeldertafel berechnet werden. Es gilt, am Beispiel der bedingten Wahrscheinlichkeit von $B$ unter der Bedingung von $A$:
$P(B|A)=\frac{|A\cap B|}{|A|}$.
Ebenso können auch die übrigen bedingten Wahrscheinlichkeiten berechnet werden.
Auch dies schauen wir uns an dem Beispiel zum Frühstücksverhalten an:

- Wie groß ist die Wahrscheinlichkeit, dass eine Person, die mindestens fünfmal pro Woche frühstückt, eine Frau ist?
$\quad~~~P(W|F)=\frac{|F\cap W|}{|F|}=\frac{180}{250}=0,72$.
- Wie groß ist die Wahrscheinlichkeit, dass ein Mann mindestens fünfmal pro Woche frühstückt?
$\quad~~~P(F|\bar{W})=\frac{|F\cap \bar{W}|}{|\bar{W}|}=\frac{70}{230}\approx0,30$.
Der Zusammenhang zwischen Vierfeldertafeln und Baumdiagrammen
Du kannst die relativen Häufigkeiten oder Wahrscheinlichkeiten auch in Form eines Baumdiagramms darstellen.
In den Feldern einer Vierfeldertafel können auch Wahrscheinlichkeiten stehen:

Hier siehst du das zugehörige Baumdiagramm:
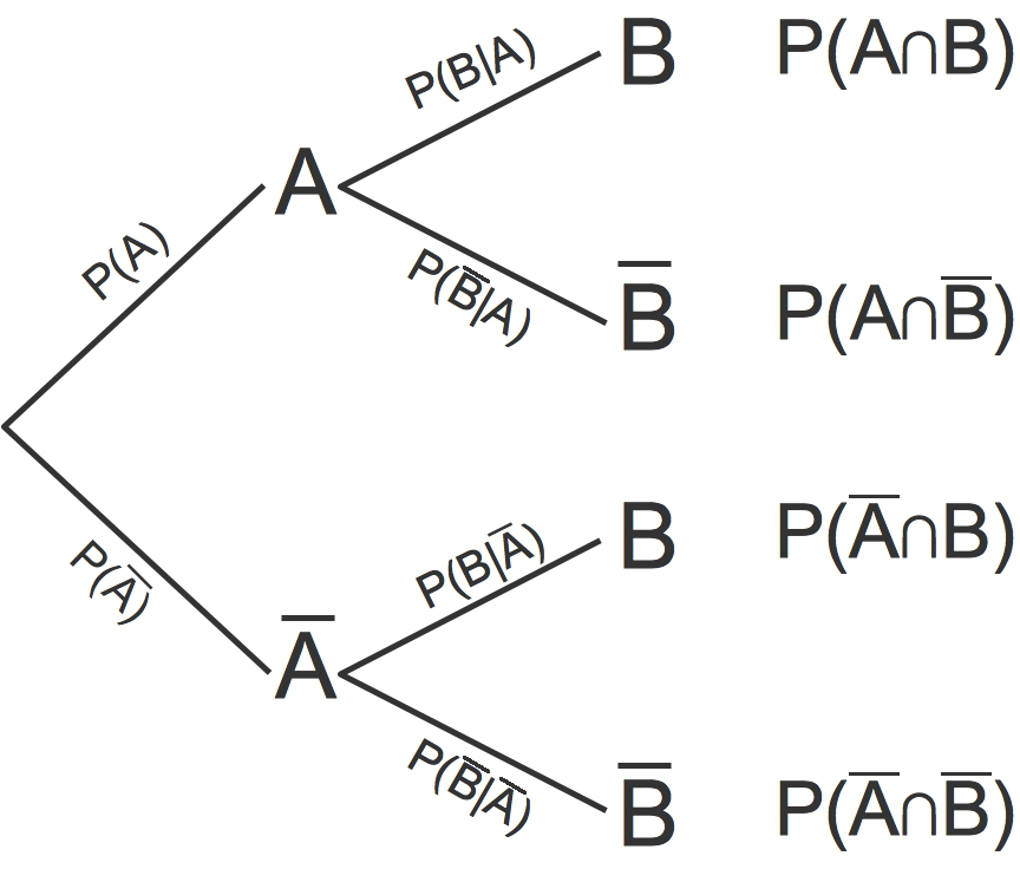
Nun kannst du mit Hilfe dieses Baumdiagramms bedingte Wahrscheinlickeiten berechnen. Es ist zum Beispiel mit dem Multiplikationssatz
$\quad~~~P(A\cap B)=P(A)\cdot P(B|A)$.
Nun kannst du diese Gleichung nach der bedingten Wahrscheinlichkeit $P(B|A)$ umstellen:
$\quad~~~P(B|A)=\frac{P(A\cap B)}{P(A)}$.
Dies entspricht gerade der bedingten Wahrscheinlichkeit, die mit Hilfe der absoluten Häufigkeiten berechnet wird:
$\quad~~~P(B|A)=\frac{|A\cap B|}{|A|}$.
Alle Videos zum Thema
Videos zum Thema
Vierfeldertafel (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Vierfeldertafel (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter






 Vierfeldertafel – Einführung
Vierfeldertafel – Einführung
 Vierfeldertafel – Übungen
Vierfeldertafel – Übungen
 Baumdiagramm in Vierfeldertafel übersetzen
Baumdiagramm in Vierfeldertafel übersetzen









