Stochastische Unabhängigkeit
Die stochastische Unabhängigkeit beschreibt den Zusammenhang zwischen den Wahrscheinlichkeiten des Eintretens zweier Ereignisse.
Beliebteste Videos
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was bedeutet stochastische Unabhängigkeit?
Die stochastische Unabhängigkeit ist nicht zu verwechseln mit kausaler Unabhängigkeit. Also der Art von Unabhängigkeit, die man aus dem Alltag kennt. Die stochastische Unabhängigkeit beschreibt den Zusammenhang zwischen den Wahrscheinlichkeiten des Eintretens zweier Ereignisse.
Anschaulich sind zwei Ereignisse stochastisch unabhängig, wenn das Eintreten eines Ereignisses die Wahrscheinlichkeit des Eintretens eines anderen Ereignisses nicht beeinflusst.
Zwei Ereignisse $A$ und $B$ sind stochastisch unabhängig, wenn gilt:
$P(A\cap B)=P(A) \cdot P(B)$.
Die Wahrscheinlichkeit, dass beide Ereignisse eintreten, ist also gleich dem Produkt ihrer Einzelwahrscheinlichkeiten. Das Eintreffen oder Nichteintreffen von Ereignis $A$ ist nicht Bedingung für das Eintreffen oder Nichteintreffen von Ereignis $B$.
Die bedingte Wahrscheinlichkeit
Seien $P(A)$ und $P(B)$ ungleich Null. Die bedingte Wahrscheinlichkeit für $A$ unter der Bedingung von $B$ ist definiert mit:
$P(A| B)=\frac{P(A\cap B)}{P(B)}$.
Analog gilt für die Wahrscheinlichkeit von $B$ unter der Bedingung von $A$:
$P(B| A)=\frac{P(A\cap B)}{P(A)}$.
Sind jetzt die Ereignisse $A$ und $B$ stochastisch unabhängig voneinander, ergibt sich für die jeweiligen bedingten Wahrscheinlichkeiten:
$P(A| B)=\frac{P(A\cap B)}{P(B)}=\frac{P(A)\cdot P(B)}{P(B)}=P(A)$ und
$P(B| A)=\frac{P(A\cap B)}{P(A)}=\frac{P(A)\cdot P(B)}{P(A)}=P(B)$.
Sind zwei Ereignisse nicht stochastisch unabhängig, sind sie stochastisch abhängig.
Für zwei stochastisch abhängige Ereignisse $A$ und $B$ gilt:
$P(A\cap B)\neq P(A) \cdot P(B).$
Zwei Ereignisse $A$ und $B$ heißen demnach stochastisch abhängig, wenn die Gleichung der stochastischen Unabhängigkeit nicht erfüllt ist. Die Wahrscheinlichkeit des Eintretens beider Ereignisse ist ungleich dem Produkt der beiden Einzelwahrscheinlichkeiten.
Baumdiagramm und Vierfeldertafel
Mit Hilfe eines Baumdiagrammes oder einer Vierfeldertafel kannst du bedingte Wahrscheinlichkeiten überprüfen. Schau dir das Baumdiagramm der bedingten Wahrscheinlichkeiten zweier Ereignisse $A$ und $B$ an.
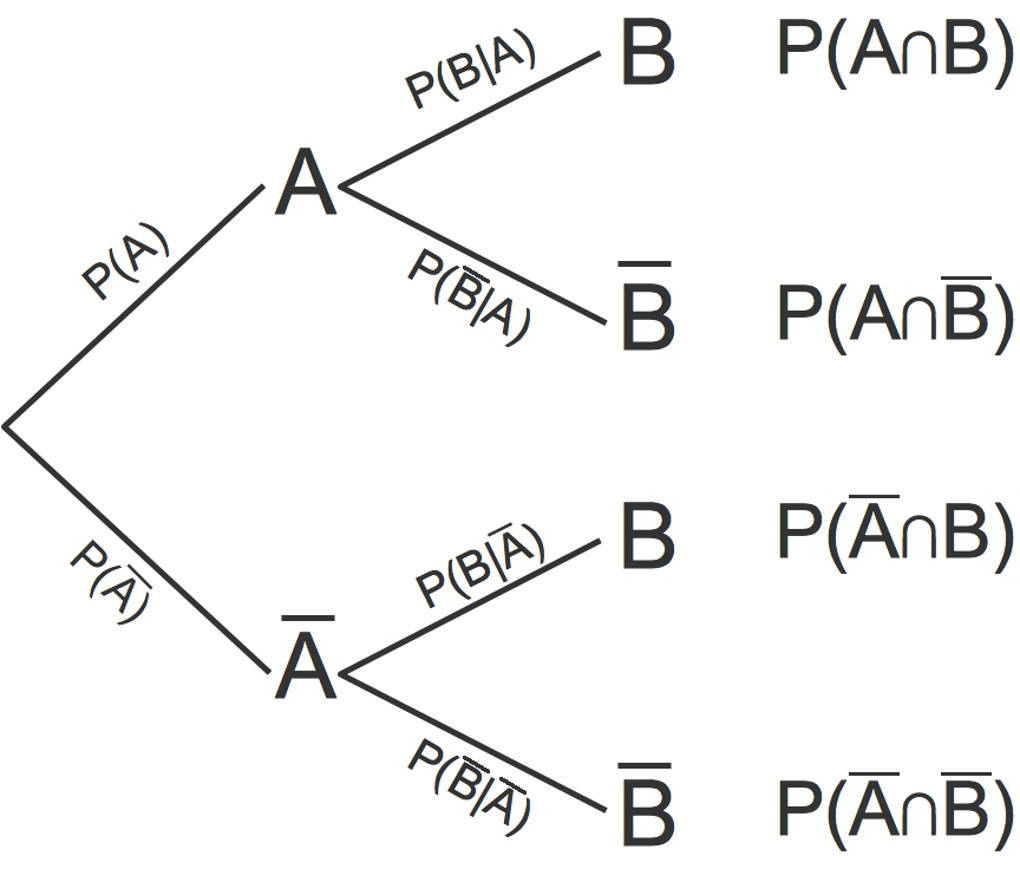
Sind die beiden Ereignisse $A$ und $B$ stochastisch unabhängig, dann ist die Wahrscheinlichkeit des Eintretens von $B$ im $2.$ Zug unabhängig davon, ob im $1. $Zug das Ereignis $A$ oder das Gegenereignis $\overline{A}$ eintritt. In beiden Fällen ist die Wahrscheinlichkeit gleich:
$P(B| A)=P(B| \overline{A})=P(B)$.
Analog gilt für $\overline{B}$:
$P(\overline{B}| A)=P(\overline{B}| \overline{A})=P(\overline{B})$.
Sind zwei Ereignisse $A$ und $B$ stochastisch unabhängig, so sind auch $A$ und $\overline{B}$, $\overline{A}$ und $\overline{B}$, sowie $\overline{A}$ und $B$ stochastisch unabhängig.
Werden nun die Durchschnittswahrscheinlichkeiten der zwei stochastisch unabhängigen Ereignisse $A$ und $B$ nach dem Multiplikationssatz betrachtet, dann gilt:
$P(A\cap B)=P(A) \cdot P(B|A)=P(A) \cdot P(B)$
$P(\overline{A}\cap B)=P(\overline{A}) \cdot P(B|\overline{A})=P(\bar{A}) \cdot P(B)$
$P(A\cap \overline{B})=P(A) \cdot P(\overline{B}|A)=P(A) \cdot P(\overline{B})$
$P(\bar{A}\cap \overline{B})=P(\overline{A}) \cdot P(\overline{B}|\overline{A})=P(\overline{A}) \cdot P(\overline{B})$
Sind zwei Ereignisse stochastisch unabhängig, dann sind Wahrscheinlichkeiten in den einzelnen Feldern der Vierfeldertafel gleich dem Produkt der Wahrscheinlichkeiten der zugehörigen Spalte und der zugehörigen Zeile. Die Vierfeldertafel kann genutzt werden, um die Unabhängigkeit von Ereignissen zu überprüfen.
\begin{array}{c|c|c|c} ~~&A & \bar{A} & ~~ \\ \hline B& P(A\cap B) & P(\overline {A} \cap B)& P(B) \\ \hline \overline{B} & P(A\cap \overline{B}) & P(\overline{A} \cap \overline{B}) & P(\overline{B}) \\ \hline ~~ & P(A) & P(\overline{A}) & ~~ \end{array}
Eigenschaften der stochastischen Unabhängigkeit
- Ist ein Ereignis $A$ stochastisch unabhängig von einem Ereignis $B$, dann ist $B$ auch stochastisch unabhängig von $A$. Die stochastische Unabhängigkeit ist symmetrisch.
- Sind zwei Ereignisse $A$ und $B$ stochastisch unabhängig mit $P(B)>0$, so ist die Wahrscheinlichkeit des Eintretens des Ereignisses $A$ unabhängig davon, ob Ereignis $B$ oder das Gegenereignis $\bar{B}$ eintritt. Für das Gegenereignis $\bar{B}$ gilt die Komplementärregel. Es gilt für die bedingte Wahrscheinlichkeit:
$~~~~~~P(A| B)=P(A| \overline{B})=P(A)$.
Nun werden die Sonderfälle $P(A)=0$ und $P(A)=1$ betrachtet.
- Ein Ereignis $A$ ist genau dann von sich selbst unabhängig, wenn es mit Wahrscheinlichkeit $P(A)=1 $ oder $P(A)=0$ eintritt.
- Die leere Menge $\emptyset$ und die Grundmenge $\Omega$ sind immer zu sich selbst unabhängig.
- Ist ein Ereignis $A$ von einem beliebigen Ereignis $B$ unabhängig, so gilt für $A$:
$~~~~~~P(A) =1$ oder
$~~~~~~P(A)=0.$
- Hat ein Ereignis $A$ die Wahrscheinlichkeit $P(A)=0$ oder $P(A)=1$, so gilt für ein beliebiges Ereignis $B$, dass $A$ und $B$ stochastisch unabhängig sind.
$~~~~~~$Für $P(A)=0$ gilt: $P(A\cap B)=0$.
$~~~~~~$Und für $P(A)=1$ gilt: $P(A\cap B)=1$.
Stochastische Unabhängigkeit überprüfen - Beispiel
Stochastische Unabhängig kannst du prüfen durch die Anwendung der Formel zur stochastischen Unabhängigkeit.

Montags fehlen Tim und Jerry regelmäßig in der Schule. Tim ist mit einer Wahrscheinlichkeit von $0,75$ in der Schule anwesend. Jerry fehlt mit einer Wahrscheinlichkeit von $0,3$ montags. Die Wahrscheinlichkeit, dass beide nicht in der Schule sind, liegt bei $0,2$. Ist die Abwesenheit von Tim und Jerry stochastisch abhängig oder stochastisch unabhängig?
Ereignis $A$ ist die Anwesenheit von Tim an einem Montag. Ereignis $B$ ist die Abwesenheit von Jerry an einem Montag. Da geprüft werden soll, ob die Abwesenheit der beiden stochastisch unabhängig ist, muss gezeigt werden, ob die Bedingung der stochastischen Unabhängigkeit erfüllt ist:
$P(\overline{A}\cap B)=P(\overline{A}) \cdot P(B).$
Da die Abwesenheit von Tim gesucht ist, wird das Gegenereignis $\bar{A}$ betrachtet. Die Wahrscheinlichkeit von $\bar{A}$ wird bestimmt mit:
$P(\overline{A})=1-P(A)=1-0,75 =0,25.$
Die Wahrscheinlichkeit, dass Jerry nicht zur Schule kommt, ist gegeben mit $P(B)=0,3$. Die Wahrscheinlichkeit, dass beide abwesend sind, ist gegeben mit $P(\bar{A}\cap B)=0,2$.
Werden nun die Werte der Wahrscheinlichkeiten für die Abwesenheit von Tim $(P(\bar{A}))$, die Abwesenheit von Jerry $(P(B))$ und die Abwesenheit von beiden $(P(\bar{A}\cap B))$ in die Gleichung der stochastischen Unabhängigkeit eingesetzt, ergibt sich:
\begin{array}{c c c} P(\bar{A}\cap B) & = & P(\bar{A}) \cdot P(B)\\ 0,2 & = & 0,3 \cdot 0,25\\ 0,2 &\neq & 0,075 \end{array}
Die Bedingung zur stochastischen Unabhängigkeit ist nicht erfüllt. Die Abwesenheit von Tim und Jerry ist stochastisch abhängig voneinander. Dies bedeutet jedoch nicht, dass die Abwesenheit der beiden in einer kausalen Abhängigkeit stehen muss. Tim und Jerry haben einen unterschiedlichen Freundeskreis, Schulweg und auch sonst keinerlei Gemeinsamkeiten, die einen Einfluss auf die Abwesenheit haben würden. Zwei Ereignisse können also stochastisch abhängig voneinander sein ohne, dass ein kausaler Zusammenhang besteht.
Alle Videos zum Thema
Videos zum Thema
Stochastische Unabhängigkeit (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Stochastische Unabhängigkeit (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter







 Stochastische Unabhängigkeit – Einführung
Stochastische Unabhängigkeit – Einführung
 Stochastische Unabhängigkeit – Baumdiagramm und Vierfeldertafel
Stochastische Unabhängigkeit – Baumdiagramm und Vierfeldertafel
 Stochastische Unabhängigkeit – Beispielaufgabe
Stochastische Unabhängigkeit – Beispielaufgabe









