Rekonstruktion ganzrationaler Funktionen – Pipeline

Rekonstruktion ganzrationaler Funktionen – Pipeline Übung

• Stelle das Gleichungssystem zur Rekonstruktion der Funktion auf.

  Tipps

  „Ohne Knick“ bedeutet, dass sowohl die Funktionswerte als auch die Ableitungen an dieser Stelle übereinstimmen.

  Die Ableitung von $f(x)$ ist $f'(x)=3ax^2+2bx+c$.

  Die Ableitung einer linearen Funktion ist der Faktor vor dem $x$.

  Lösung

  An jeder der beiden Stellen müssen sowohl die Funktionswerte als auch die Ableitungen übereinstimmen.

  Betrachten wir zunächst die Stelle $x=1$:

  • $g(1)=-1$, daher muss $f(1)=-1$ gelten. Dies führt zu $a \cdot 1^3+b\cdot 1^2+c\cdot 1+d \\ = a+b+c+d=-1$
  • $g'(1)=-1$, und damit muss auch $f'(1)=-1$ gelten. So erhält man $3a\cdot 1^2+2b\cdot 1+c=-1$, also $3a+2b+c=-1$.

  Ebenso können die Gleichungen an der anderen Stelle mit $h(x)$ aufgestellt werden:

  Betrachten wir nun die Stelle $x=5$:

  • $h(5)=2\cdot 5-5=5$ und somit ist $f(5)=5$. Dies führt zu $a\cdot 5^3+b\cdot 5^2+c\cdot 5+d=125a+25b+5c+d=5$.
  • $h'(5)=2$ und damit auch $f'(5)=2$. So erhält man $3a\cdot 5^2+2b\cdot 5+c=75a+10b+c=2$.

  Dies kann man nun als lineares Gleichungssystem aufschreiben:

  $\begin{array}{rcrcrcrcr} a&+&b&+&c&+&d&=&-1 \\ 3a&+&2b&+&c&&&=&-1 \\ 125a&+&25b&+&5c&+&d&=&5 \\ 75a&+&10b&+&c&&&=&2 \end{array}$

• Ermittle die Funktionsgleichung der kubischen Funktion $f(x)=ax^3+bx^2+cx+d$ durch Lösen des linearen Gleichungssystems.

  Tipps

  Du kannst eine Kontrolle durchführen. Überprüfe, ob diese Eigenschaften erfüllt sind:

  • $f(1)=-1$
  • $f'(1)=-1$
  • $f(5)=5$
  • $f'(5)=2$

  Wenn du eine Unbekannte ermittelt hast, kannst du diese in eine Gleichung einsetzen, in welcher sie vorkommt. Eine weitere noch unbekannte Variable kannst du so ermitteln.

  Zur Bestimmung von $d$ kannst du zum Beispiel bei bekannten Werten für $a$, $b$ und $c$ die erste Gleichung

  $a+b+c+d=-1$

  verwenden.

  Lösung

  Wenn man von der ersten Gleichung die dritte subtrahiert, fällt $d$ weg:

  $(5)~~$ $-124a-24b-4c=-6$.

  Ebenso kann man von der zweiten die dritte Gleichung subtrahieren. So eliminiert man $c$:

  $(6)~~$ $-72a-8b=-3$.

  Umformen der zweiten Gleichung nach $c$ führt zu

  $c=-1-3a-2b$.

  Dieses $c$ wird in die fünfte Gleichung eingesetzt:

  $-124a-24b-4(-1-3a-2b)=-6$.

  Durch Auflösen der Klammern und Zusammenfassen der Terme erhält man

  $-124a-24b+4+12a+8b=-112a-16b+4=-6$, also $-112a-16b=-10$.

  Diese Gleichung wird nun noch nach $b$ umgestellt:

  $b=\frac{10}{16}-\frac{112}{16}a$.

  Dies setzen wir in die sechste Gleichung ein:

  $-72a-8\left(\frac{10}{16}-\frac{112}{16}a\right)=-3$.

  Also ergibt sich $a$ wie folgt

  $\begin{array}{lrclll} &-72a-8\left(\frac{10}{16}-\frac{112}{16}a\right)&=&-3\\ \Leftrightarrow&-72a-5+56a&=&-3\\ \Leftrightarrow&-16a-5&=&-3&|&+5\\ &-16a&=&2&|&:(-16)\\ &a&=&-\frac18 \end{array}$

  Nun kann dieses $a$ unter anderem in die sechste Gleichung eingesetzt werden. Dann wird nach $b$ umgeformt:

  $\begin{array}{lrclll} &-72\cdot \left(-\frac18\right)-8b&=&-3\\ \Leftrightarrow&9-8b&=&-3&|&-9\\ &-8b&=&-12&|&:(-8)\\ &b&=&\frac32 \end{array}$.

  $a$ und $b$ werden in $c=-1-3a-2b$ eingesetzt:

  $c=-1-3\cdot\left(-\frac18\right)-2\cdot \frac32=-\frac{29}8$.

  Zuletzt werden $a$, $b$ und $c$ in die erste Gleichung eingesetzt:

  $-\frac18+\frac32-\frac{29}8+d=-1$.

  Dies führt zu $d=\frac54=\frac{10}8$.

• Stelle die Bedingungen auf, welche die quadratische Funktion erfüllen muss.

  Tipps

  In dem Punkt, in welchem die Gerade und die Parabel ineinander übergehen, müssen deren Steigungen übereinstimmen, damit kein Knick entsteht.

  Wenn ein Punkt auf dem Funktionsgraphen einer Funktion $f(x)$ liegt, ist der Funktionswert an der x-Koordinate gerade die y-Koordinate des Punktes.

  Die Steigung der gestrichelten Geraden wird nicht benötigt.

  Lösung

  Die Funktionsgleichung der Parabel lautet

  $f(x)=ax^2+bx+c$.

  Die Geradengleichung ist gegeben durch $g(x)=3-2x$. Damit ist

  • $h(0)=3$ und
  • $h'(0)=-2$.

  Man kann mit den Bedingungen bei $x=0$ beginnen:

  • $f(0)=3$, da die Funktionswerte übereinstimmen müssen.
  • $f'(0)=-2$, da die Ableitungen an dieser Stelle auch übereinstimmen müssen.

  Nun kann man sich die Bedingung an der Stelle $x=3$ anschauen:

  $f(3)=1,5$.

  Diese drei Bedingungen führen zu Gleichungen, mittels derer die Funktionsgleichung der Parabel hergeleitet werden kann.

• Leite die Gleichung der Parabel sowie der Geraden, welche die Straße fortsetzt, her.

  Tipps

  Setze die jeweiligen bekannten Werte für $x$ in die Funktionsgleichung ein.

  Es ist $f'(x)=2ax+b$ im Fall der Parabel.

  Die rechte Gerade muss an der Stelle $x=3$ die gleiche Steigung haben wie die Parabel.

  Lösung

  Die Bedingungen für die Funktionsgleichung der Parabel sind bereits bekannt:

  • $f(0)=3$: Wir können die Gleichung $a\cdot 0^2+b\cdot 0+c=3$ aufstellen. Diese führt zu $c=3$.
  • $f'(0)=-2$: Mit $f'(x)=2ax+b$ folgt damit $b=-2$.

  Somit haben wir die gesuchte Parabelgleichung schon so weit aufgestellt:

  $f(x)=ax^2-2x+3$.

  Nun kann noch die dritte Bedingung $f(3)=1,5$ verwendet werden:

  $a\cdot 3^2-2\cdot 3+3=1,5$.

  Dies führt zu $9a-6+3=1,5$ und nach Umformungen zu $a=0,5$.

  Die gesuchte Funktionsgleichung lautet somit $f(x)=0,5x^2-2x+3$.

  Deren Ableitung ist $f'(x)=x-2$.

  An der Stelle $x=3$ muss die rechte Gerade $h(x)=mx+b$ tangential an die Parabel anschließen. Dadurch haben wir zwei Bedingungen:

  • $m=f'(3)=3-2=1$
  • $h(3)=1,5$

  So folgt $h(3)=3+b=1,5$. Subtraktion von $3$ resultiert in $b=-1,5$.

  Somit lautet die gesuchte Geradengleichung $h(x)=x-1,5$.

• Beschreibe, wie sich ein Knick vermeiden lässt.

  Tipps

  Du kannst dir „ohne Knick“ so vorstellen: Wenn du auf Rollschuhen (oder womit auch immer) eine Strecke fährst, rollst du ganz ruhig.

  • Du springst keinen Berg herunter und
  • du spürst keine Unebenheiten.

  Wenn die Funktionswerte nicht übereinstimmen, liegt eine Sprungstelle vor.

  Die Gerade muss eine Tangente der kubischen oder quadratischen Funktion an dieser Stelle sein.

  Die Steigung einer Tangente ist die Ableitung der Funktion an der entsprechenden Stelle.

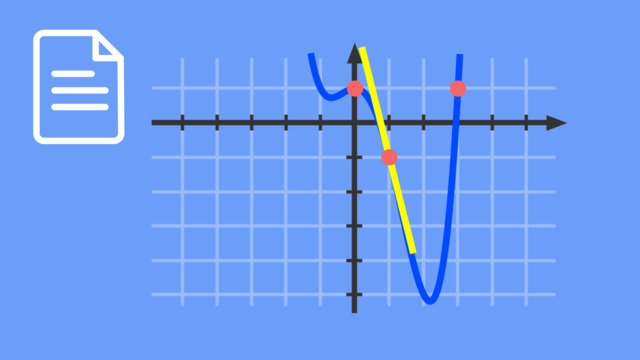
  Lösung

  In dem Bild ist zu erkennen, dass

  • zum einen die Funktionswerte der grünen als auch blauen Funktion an der Stelle, an welcher sie aufeinander treffen, übereinstimmen, und
  • zum anderen die blaue Gerade und die grüne Gerade an dieser Stelle dieselbe Steigung besitzen. Wir können auch sagen: Die blaue Gerade ist an der Stelle, wo der grüne Graph aufhört, eine Tangente.

  Was bedeutet es noch, wenn die blaue Gerade eine Tangente der grünen Funkion ist? Richtig: Die Ableitungen der beiden Funktionen stimmen überein.

  • Wenn die Funktionswerte nicht übereinstimmen würden, würde eine Sprungstelle vorliegen.
  • Wenn die Ableitungen nicht übereinstimmen, entsteht ein Knick.

• Leite die Funktionsgleichung der kubischen Funktion her, welche die Sprungschanze beschreibt.

  Tipps

  Die beiden Werte für $c$ und $d$ kannst du mehr oder weniger ablesen.

  Die erste Ableitung der Funktion ist

  $f'(x)=3ax^2+2bx+c$.

  Wenn ein Punkt $P(p_x|p_y)$ auf dem Funktionsgraphen von $f(x)$ liegt, dann gilt $f(p_x)=p_y$.

  Eine der beiden Gleichungen zur Bestimmung von $a$ und $b$ lautet

  $216000a+3600b=-75$.

  Lösung

  Was ist bereits bekannt für die Sprungschanze?

  1. $f(0)=100$
  2. $f'(0)=0$
  3. $f(60)=25$
  4. $f'(60)=0,1$

  Aus der ersten Gleichung folgt $d=100$.

  Die erste Ableitung von $f(x)$ ist $f'(x)=3ax^2+2bx+c$.

  Somit folgt mit der zweiten Gleichung, dass $c=0$ ist.

  Nun kann die Funktionsgleichung mit diesen beiden Werten bereits aufgeschrieben werden:

  • $f(x)=ax^3+bx^2+100$
  • sowie deren Ableitung $f'(x)=3ax^2+2bx$.

  Nun können die dritte und vierte Bedingung betrachtet werden. Dies führt zu den folgenden Gleichungen:

  (I) $216000a+3600b=-75$

  (II) $10800a+120b=0,1$

  Wenn man das $30$-fache der zweiten Gleichung von der ersten subtrahiert, erhält man

  $-108000a=-78$.

  Division durch $-108000$ führt zu

  $a=\frac{78}{108000}=0,0007\bar2\approx0,0007$.

  Zuletzt wird dieser Wert von $a$ in der ersten Gleichung eingesetzt. Dies führt zu

  $216000\cdot \frac{78}{108000}+3600b=-75$.

  Dies kann umgeformt werden zu $b=-\frac{77}{1200}\approx0,064$.

  Insgesamt lautet die Funktionsgleichung

  $f(x)=0,0007x^3-0,064x^2+100$.