Polarkoordinaten
- Polarkoordinaten – benötigtes Vorwissen
- Was sind Polarkoordinaten?
- Umwandlung der Koordinatenformen
- Kartesische Koordinaten in Polarkoordinaten umwandeln
- Polarkoordinaten in kartesische Koordinaten umwandeln
- Umwandlung der Koordinaten – Beispiele
- Beispielrechnung – kartesische Koordinaten in Polarkoordinaten umwandeln
- Beispielrechnung – Polarkoordinaten in kartesische Koordinaten umwandeln
- Polarkoordinaten – Zusammenfassung
- Häufig gestellte Fragen zum Thema Polarkoordinaten
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Lerntext zum Thema Polarkoordinaten
Polarkoordinaten – benötigtes Vorwissen
Für dieses Thema solltest du wissen, wie die Verhältnisse Sinus, Cosinus und Tangens im rechtwinkligen Dreieck definiert sind. Zur Erinnerung:
In einem rechtwinkligen Dreieck lassen sich folgende Seitenverhältnisse aufstellen:
$\sin(\alpha) = \dfrac{\text{Gegenkathete}}{\text{Hypotenuse}}$
$\cos(\alpha) = \dfrac{\text{Ankathete}}{\text{Hypotenuse}}$
$\tan(\alpha) = \dfrac{\text{Gegenkathete}}{\text{Ankathete}}$
Außerdem solltest du wissen, was der Einheitskreis ist. Dieser ist ein Kreis im Koordinatensystem mit dem Radius $1$ und dem Ursprung als Mittelpunkt.
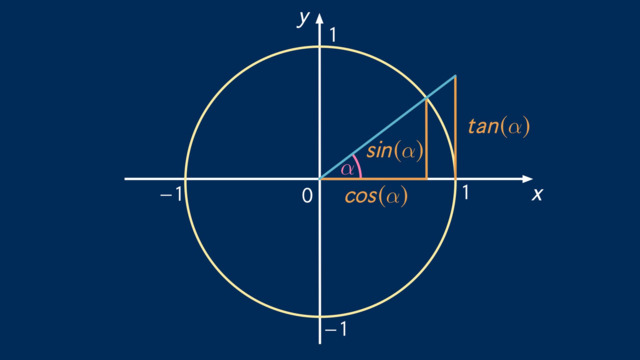
Wiederholung – Sinus, Cosinus und Tangens am Einheitskreis
Man kann in den Einheitskreis ein rechtwinkliges Dreieck einzeichnen, indem man einen Winkel $\alpha$ von der positiven $x$-Achse aus einzeichnet und den Winkelschenkel bis zur Kreislinie zeichnet. Dieser stellt die Hypotenuse dar. Das Lot von dem Schnittpunkt mit der Kreislinie aus zur $x$-Achse stellt dann die dritte Seite des rechtwinkligen Dreiecks dar.
Da die Hypotenuse dem Radius des Einheitskreises entspricht und dieser per Definition die Länge $1$ hat, ist die Länge der Hypotenuse auf $1$ festgelegt. Die Gleichungen für Sinus und Cosinus verkürzen sich damit:
$\sin(\alpha) = \dfrac{\text{Gegenkathete}}{\text{Hypotenuse}} = \dfrac{\text{Gegenkathete}}{1} = \text{Gegenkathete}$
$\cos(\alpha) = \dfrac{\text{Ankathete}}{\text{Hypotenuse}} = \dfrac{\text{Ankathete}}{1} = \text{Ankathete}$
Den Tangens kann man ebenfalls im Einheitskreis darstellen, indem man den zweiten Strahlensatz nutzt.
Damit kann man diese Gleichung aufstellen:
$\dfrac{\tan(\alpha)}{1} = \dfrac{\text{Gegenkathete}}{\text{Ankathete}} \Leftrightarrow \tan(\alpha) = \dfrac{\sin(\alpha)}{\cos(\alpha)}$
Was sind Polarkoordinaten?
Bisher hast du Punkte im Koordinatensystem stets durch kartesische Koordinaten angegeben. Die Lage eines Punkts im Koordinatensystem ist dabei durch seine $x$- und $y$-Koordinaten eindeutig bestimmt, allgemein sieht das so aus: $P(x\vert y)$.
Man kann Punkte aber auch anders eindeutig angeben, und zwar durch die sogenannten Polarkoordinaten.
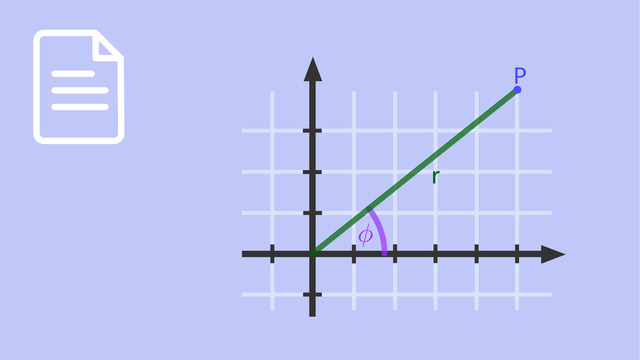
Die Polarkoordinaten eines Punkts $P$ sind zum einen durch die Strecke der Länge $r$ bestimmt, die vom Ursprung aus bis zum Punkt $P$ verläuft. Der Winkel $\phi$, der von dieser Strecke und der $x$-Achse eingeschlossen wird, beschreibt die zweite Polarkoordinate. Der Punkt $P$ kann also auch eindeutig beschrieben werden durch: $P(r\vert\phi)$.
Umwandlung der Koordinatenformen
Für Koordinaten mit $x~\neq~0$ können kartesische Koordinaten in Polarkoordinaten umgewandelt werden und andersherum.
Kartesische Koordinaten in Polarkoordinaten umwandeln
Nun wollen wir die kartesischen Koordinaten in Polarkoordinaten umwandeln. Wenn $x$ und $y$ gegeben sind, können wir $r$ leicht bestimmen, indem wir ein rechtwinkliges Dreieck in das Koordinatensystem zeichnen.
Dadurch können wir zunächst die kartesischen Koordinaten in die Polarkoordinaten umwandeln. Mit dem Satz des Pythagoras gilt:
$r^{2} = x^{2} + y^{2} \Rightarrow r = \sqrt{x^{2} + y^{2}}$
Weiterhin kann man mit dem Tangens folgende Gleichung aufstellen:
$\tan(\phi) = \dfrac{\text{Gegenkathete}}{\text{Ankathete}} = \dfrac{y}{x} \Rightarrow \phi = \arctan\left(\dfrac{y}{x}\right)$
Polarkoordinaten in kartesische Koordinaten umwandeln
Mithilfe von Sinus und Cosinus können schließlich die Polarkoordinaten in die kartesischen Koordinaten umgewandelt werden. Denn mit dem obigen Dreieck gilt:
$\cos(\phi) = \dfrac{\text{Ankathete}}{\text{Hypotenuse}} = \dfrac{x}{r} \Rightarrow x = r \cdot cos(\phi)$
$\sin(\phi) = \dfrac{\text{Gegenkathete}}{\text{Hypotenuse}} = \dfrac{y}{r} \Rightarrow y = r \cdot \sin(\phi)$
Umwandlung der Koordinaten – Beispiele
Die Umwandlungen in beide Richtungen wollen wir nun an ein paar Beispielrechnungen verdeutlichen.
Beispielrechnung – kartesische Koordinaten in Polarkoordinaten umwandeln
Nehmen wir als erstes Beispiel den Punkt $A(4\vert3)$. Bei diesem wollen wir die kartesischen Koordinaten in Polarkoordinaten umwandeln. Dafür nutzen wir die Gleichungen von oben:
$r = \sqrt{x^{2} + y^{2}} = \sqrt{4^{2} + 3^{2}} = \sqrt{25} = 5$
$\phi = \arctan\left(\dfrac{y}{x}\right) = \arctan\left(\dfrac{3}{4}\right) = 36,87^\circ$
Also kann man den Punkt $A(4\vert3)$, der in kartesischen Koordinaten angegeben ist, auch eindeutig mit Polarkoordinaten beschreiben als $A(5\vert36,87^\circ)$.
Beispielrechnung – Polarkoordinaten in kartesische Koordinaten umwandeln
Umgekehrt machen wir es bei dem Punkt $B(2\vert60^\circ)$, der in Polarkoordinaten angegeben ist:
$x = 2 \cdot \cos(60^\circ) = 2 \cdot \dfrac{1}{2} = 1$
$y = 2 \cdot \sin(60^\circ) = 2 \cdot \dfrac{\sqrt{3}}{2} = \sqrt{3}$
Also lässt sich der Punkt $B(2\vert60^\circ)$ auch mit kartesischen Koordinaten schreiben als $B(1~\vert~\sqrt{3})$.
Polarkoordinaten – Zusammenfassung
Punkte können in einem Koordinatensystem durch die bereits bekannten kartesischen Koordinaten mit $P(x\vert y)$ eindeutig angegeben werden. Weiterhin können sie jedoch auch durch die Polarkoordinaten mit $P(r\vert\phi)$ eindeutig angegeben werden. $r$ ist dabei die Länge der Strecke, die den Punkt mit dem Ursprung verbindet, und $\phi$ ist der Winkel, der von der Strecke und der $x$-Achse eingeschlossen wird.
Die Polarkoordinaten und kartesischen Koordinaten können ineinander umgewandelt werden, wie die folgende Tabelle zeigt:
| Kartesische Koordinaten | Polarkoordinaten |
|---|---|
| $x = r \cdot \cos(\phi)$ | $r = \sqrt{x^{2} + y^{2}}$ |
| $y = r \cdot \sin(\phi)$ | $\phi = \arctan(\frac{y}{x})$ |
Häufig gestellte Fragen zum Thema Polarkoordinaten
Polarkoordinaten Übung
-
Vervollständige die Umwandlung von kartesischen Koordinaten in Polarkoordinaten und umgekehrt.
TippsJeder Punkt im Koordinatensystem ist eindeutig gegeben durch
- seine kartesischen Koordinaten oder
- seine Polarkoordinaten.
Ein Punkt in Polarkoordinaten ist gegeben durch $P(r;\varphi)$. Dabei ist $r$ der Abstand des Punktes zum Koordinatenursprung und der Drehwinkel $\varphi$ der von der positiven x-Achse sowie der Strecke $\overline {0P}$ eingeschlossene Winkel.
Von den kartesischen Koordinaten zu den Polarkoordinaten benötigst du
- den Satz des Pythagoras und
- $\tan(\alpha)=\frac{\text{Gegenkathete}}{\text{Ankathete}}$.
Von den Polarkoordinaten zu den kartesischen Koordinaten benötigst du
- $\sin(\alpha)=\frac{\text{Gegenkathete von } \alpha }{\text{Hypotenuse}}$ und
- $\cos(\alpha)=\frac{\text{Ankathete von } \alpha }{\text{Hypotenuse}}$
LösungJeder Punkt im Koordinatensystem ist eindeutig gegeben durch
- seine kartesischen Koordinaten $P(x;y)$ oder
- seine Polarkoordinaten $P(r;\varphi)$.
- $r$ ist der Abstand des Punktes zum Koordinatenursprung. Dieser Abstand kann mit dem Satz des Pythagoras berechnet werden, also $r=\sqrt{x^2+y^2}$.
- Der Drehwinkel $\varphi$ ist gegeben durch die Gleichung: $\tan(\varphi)=\frac{\text{Gegenkathete von } \varphi}{\text{Ankathete von } \varphi}=\frac yx$ für $x>0$ und $y\geq 0$. Somit ist $\varphi=\arctan\left( \frac yx\right)$.
- $\sin(\varphi)=\frac{\text{Gegenkathete von } \varphi }{\text{Hypotenuse}}$ und
- $\cos(\varphi)=\frac{\text{Ankathete von } \varphi }{\text{Hypotenuse}}$
- $x=r \cdot \cos(\varphi)$ und
- $y=r \cdot \sin(\varphi)$.
-
Stelle den gegebenen Punkt in Polarkoordinaten dar.
TippsBei gegebenen kartesischen Koordinaten gilt:
- $r=\sqrt{x^2+y^2}$ und
- $\varphi=\arctan\left( \frac yx\right)$ für $x>0$ und $y\geq 0$.
„arctan“ ist die Umkehrung von „tan“. Diese erhältst du auf deinem Taschenrechner durch die Umschalttaste „inv“, „Shift“, ...
Achte darauf, dass dein Taschenrechner auf „D“ oder „DEG“ für „Degree“, also Winkelmaß, eingestellt ist.
LösungBei gegebenen kartesischen Koordinaten gilt:
- Der Radius $r$ lässt sich berechnen durch $r=\sqrt{x^2+y^2}$ und
- der Drehwinkel $\varphi$ durch $\varphi=\arctan\left( \frac yx\right)$ für $x>0$ und $y\geq 0$.
- $r=\sqrt{3^2+4^2}=\sqrt{25}=5$ und
- $\varphi=\arctan\left( \frac yx \right)=\arctan\left( \frac 43 \right)=53{,}13^\circ$.
-
Erkläre in dem rechtwinkligen Dreieck Sinus, Kosinus und Tangens.
TippsDie Hypotenuse liegt im rechtwinkligen Dreieck dem rechten Winkel gegenüber. Sie ist die längste Seite.
Die Gegenkathete eines spitzen Winkels ist die Seite, die dem spitzen Winkel gegenüberliegt.
Die Ankathete eines spitzen Winkels ist die Seite, die an diesem Winkel anliegt.
LösungDie trigometrischen Funktionen sind in einem rechtwinkligen Dreieck für den spitzen Winkel $\alpha$ wie folgt definiert:
$\begin{align*} \sin(\alpha)&=\frac{\text{Gegenkathete von } \alpha}{\text{Hypotenuse}} \\ \cos(\alpha)&=\frac{\text{Ankathete von } \alpha}{\text{Hypotenuse}} \\ \tan(\alpha)&=\frac{\text{Gegenkathete von } \alpha}{\text{Ankathete von } \alpha} =\frac{\sin(\alpha)}{\cos(\alpha)} \end{align*}$.
Um mit den trigonometrischen Funktionen zu arbeiten, muss man sich zunächst klarmachen, welche Seiten in dem Dreieck die Katheten und welche die Hypotenuse sind. In dem obigen Dreieck sind
- die Katheten $a$ und $c$ und
- die Hypotenuse $b$. Die Hypotenuse ist die längste Seite in einem rechtwinkligen Dreieck. Sie liegt dem rechten Winkel gegenüber.
Somit gelten die folgenden Gleichungen:
$\begin{align*} \sin(\alpha)&=\frac ab\\ \cos(\alpha)&=\frac cb\\ \tan(\alpha)&=\frac ac\\ \sin(\gamma)&=\frac cb\\ \cos(\gamma)&=\frac ab\\ \tan(\gamma)&=\frac ca\\ \end{align*}$
Hier ist zu erkennen, dass $\sin(\alpha)=\cos(\gamma)$ und $\cos(\alpha)=\sin(\gamma)$ gilt.
-
Leite aus dem Punkt in Polarkoordinaten die kartesischen Koordinaten her.
TippsDie kartesischen Koordinaten lassen sich mit den Polarkoordinaten berechnen durch die Verwendung von
- $\sin(\alpha)=\frac{\text{Gegenkathete von } \alpha }{\text{Hypotenuse}}$ und
- $\cos(\alpha)=\frac{\text{Ankathete von } \alpha }{\text{Hypotenuse}}$.
Achte darauf, dass dein Taschenrechner auf „D“ oder „DEG“ für Winkelmaß eingestellt ist.
Du könntest dein Ergebnis überprüfen. Es muss gelten $x^2+y^2=r^2=25$.
Beachte: Bei gerundeten Ergebnissen wird nicht exakt 25 herauskommen.
LösungBei gegebenen Polarkoordinaten $P(r;\phi )$ können die entsprechenden kartesischen Koordinaten $P(x;y)$ wie folgt berechnet werden:
- $x=r \cdot \cos(\phi)$ und
- $y=r \cdot \sin(\phi)$.
Somit ist
- $x=5\cdot \cos(40^\circ )≈3{,}83$ und
- $y=5\cdot \sin(40^\circ )≈3{,}21$.
-
Beschreibe den Sinus, den Kosinus und den Tangens am Einheitskreis.
TippsDie trigonometrischen Funktionen sind in einem rechtwinkligen Dreieck wie folgt definiert:
$\begin{align*} \sin(\alpha)&=\frac{\text{Gegenkathete von } \alpha}{\text{Hypotenuse}} \\ \cos(\alpha)&=\frac{\text{Ankathete von } \alpha}{\text{Hypotenuse}} \\ \tan(\alpha)&=\frac{\text{Gegenkathete von } \alpha}{\text{Ankathete von } \alpha} =\frac{\sin(\alpha)}{\cos(\alpha)} \end{align*}$
Wie lang ist die Hypotenuse im Einheitskreis?
Die geometrische Bedeutung des Tangens kann mit dem 1. Strahlensatz hergeleitet werden.
LösungDie trigometrischen Funktionen sind in einem rechtwinkligen Dreieck für den spitzen Winkel $\alpha$ wie folgt definiert:
$\begin{align*} \sin(\alpha)&=\frac{\text{Gegenkathete von } \alpha}{\text{Hypotenuse}} \\ \cos(\alpha)&=\frac{\text{Ankathete von } \alpha}{\text{Hypotenuse}} \\ \tan(\alpha)&=\frac{\text{Gegenkathete von } \alpha}{\text{Ankathete von } \alpha} =\frac{\sin(\alpha)}{\cos(\alpha)} \end{align*}$
Im Einheitskreis hat die Hypotenuse die Länge 1, somit ist
- $\cos(\alpha)$ die Länge der Ankathete von $\alpha$,
- $\sin(\alpha)$ die Länge der Gegenkathete von $\alpha$ und
- $\tan(\alpha)$ die Länge der Tangente an den Einheitskreis. Dies kann mit dem 1. Strahlensatz hergeleitet werden.
-
Gib zu den gegebenen Punkten in kartesischen Koordinaten die Polarkoordinaten an.
TippsDer Radius kann mit dem Satz des Pythagoras berechnet werden.
Es gilt $\tan(\varphi )=\frac{\text{Gegenkathete von }\varphi }{\text{Ankathete von }\varphi }$.
Falls du einen negativen Winkel $\varphi$ berechnest, musst du diesen Winkel um 180° bzw. 360° weiterdrehen. Das hängt davon ab, in welchem Quadranten der Punkt liegt.
Es gilt die folgende Unterscheidung zur Berechnung des Drehwinkels:
$\varphi= \begin{cases} \arctan\left( \frac yx\right)&\text{für }x>0,~ y\geq 0\\ \arctan\left( \frac yx\right)+360°&\text{für }x>0,~ y< 0\\ \arctan\left( \frac yx\right)+180°&\text{für }x<0\\ 90°&\text{für }x=0,~ y> 0\\ 270°&\text{für }x=0,~ y< 0. \end{cases}$
LösungBei gegebenen kartesischen Koordinaten gilt
- Der Radius $r$ lässt sich berechnen durch $r=\sqrt{x^2+y^2}$ und
- der Drehwinkel $\varphi$ durch
Bei allen 4 Punkten ist der Radius gleich: $r=\sqrt{6^2+8^2}=\sqrt{100}=10$.
Zu den Drehwinkeln:
- $\mathbf{P(6;8)}$: Das ist der erste Fall und damit ist $\varphi=\arctan\left(\frac86 \right)=53{,}13^\circ$.
- $\mathbf{P(-6;8)}$: Das ist der dritte Fall und damit ist $\varphi=\arctan\left(\frac8{-6} \right)+180^\circ=-53{,}13^\circ+180^\circ=126{,}87^\circ$.
- $\mathbf{P(8;6)}$: Das ist der erste Fall und damit ist $\varphi=\arctan\left(\frac68 \right)=36{,}87^\circ$.
- $\mathbf{P(8;-{6})}$: Das ist der zweite Fall und damit ist $\varphi=\arctan\left(\frac{-6}8 \right)+360^\circ=-36{,}87^\circ +360^\circ =323{,}13^\circ$.
9'182
sofaheld-Level
6'600
vorgefertigte
Vokabeln
7'643
Lernvideos
35'607
Übungen
32'360
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?