Gleichungen umstellen

Inhaltsverzeichnis zum Thema

• Was ist eine Gleichung
• Beispiele für Gleichungen
• Termumformungen
• Äquivalenzumformungen
• Warum werden Gleichungen umgestellt?
• Gleichungen umstellen
• Beispiel 1
• Beispiel 2
• Beispiel 3

Was ist eine Gleichung

Mathematisch ist eine Gleichung eine Aussage, welche die Gleichheit zweier Terme beinhaltet: Term_links $=$ Term_rechts

Du kannst dir dies vorstellen wie eine Waage:

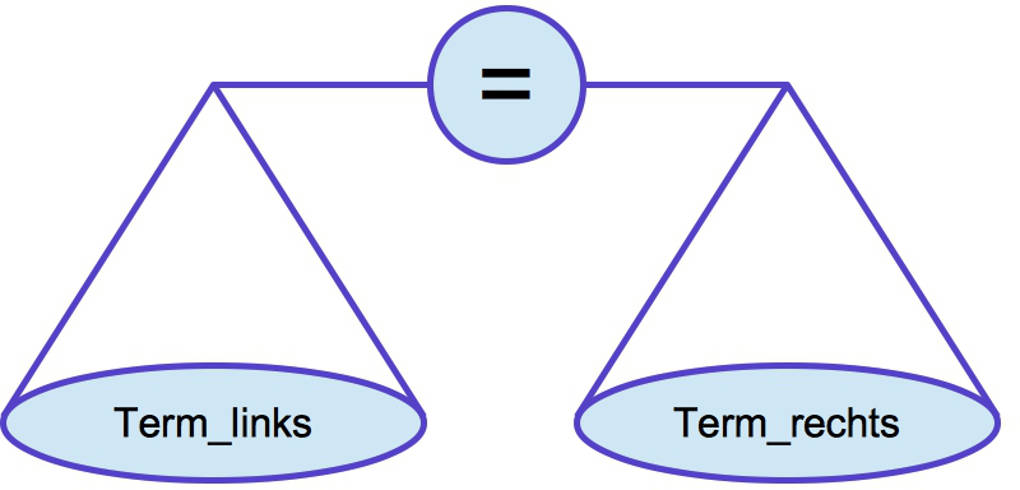
Das Gleichheitszeichen entspricht der Tatsache, dass die Waage im Gleichgewicht sein muss.

Um bei dem Bild mit der Waage zu bleiben:

• Du kannst auf einer oder auch auf beiden Seiten der Waage umräumen. Mathematisch nennt man so etwas Termumformungen.
• Du kannst auch etwas wegnehmen oder dazutun. Das musst du dann allerdings auf beiden Seiten der Waage tun. Ansonsten ist die Waage nicht mehr im Gleichgewicht.

Beispiele für Gleichungen

• $2+4=6$
• $2+x=6$
• $3x+6=24$

In den beiden unteren Gleichungen kommt jeweils eine Unbekannte, nämlich $x$, vor. Ziel ist es nun, einen Wert für $x$ zu finden, so dass die Gleichung eine wahre Aussage darstellt.

Termumformungen

Hier siehst du Beispiele für eine Termumformung:

• $3+x=x+3$: Dies ist das Kommutativgesetz oder auch Vertauschungsgesetz der Addition.
• $2(x+1)=2x+2$: Hier verwendest du das Distributivgesetz.
• $3x-4+x+5=3x+x-4+5=4x+1$: Du kannst Variablen oder Zahlen zusammenfassen.
• ...

Äquivalenzumformungen

Termumformungen sind Äquivalenzumformungen.

Weitere Äquivalenzumformungen sind:

• Du addierst oder subtrahierst auf beiden Seiten der Gleichung den gleichen Term oder die gleiche Zahl.
• Du multiplizierst beide Seiten der Gleichung mit dem gleichen Term oder der gleichen Zahl. Beachte, dass du nicht mit $0$ multiplizieren darfst.
• Du dividierst beide Seiten der Gleichung durch den gleichen Term oder die gleiche Zahl. Beachte, dass du nicht durch $0$ dividieren darfst.

Wenn du Äquivalenzumformungen durchführst, bleibt die Waage im Gleichgewicht. Das bedeutet, die Aussage der Gleichung ändert sich nicht.

Warum werden Gleichungen umgestellt?

Nun weißt du bereits, was eine Gleichung ist. Wenn in der Gleichung eine Unbekannte vorkommt, möchtest du einen Wert für diese Unbekannte finden, so dass die Gleichung eine wahre Aussage ist. Hierfür musst du die Gleichung umstellen.

Wir üben dies einmal an dem Beispiel $3x+6=24$ und schauen uns diese Gleichung erst einmal gemeinsam mit Pauls Schwester an einer Waage an. Da sie bereits weiß, wie Gleichungen umgestellt werden, erklärt sie Paul das Vorgehen:

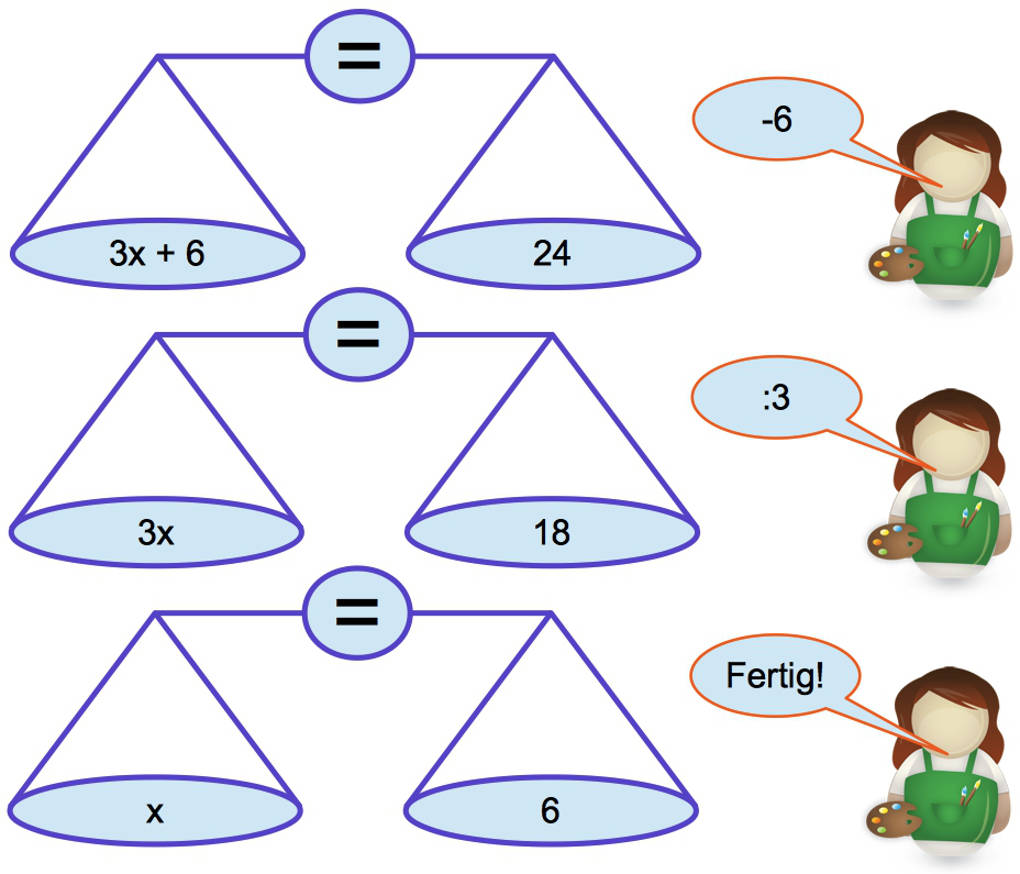
• Beachte: Wenn du addierst oder subtrahierst und multiplizierst oder dividierst, musst du dies immer auf beiden Seiten machen.
• Zuerst ziehst du auf beiden Seiten die $6$ ab. Warum? Auf der rechten Seite steht $+6$ und die Umkehrrechnung zu $+6$ ist $-6$.
• So erhältst du $3x=18$.
• Jetzt musst du noch durch $3$ teilen, da das Teilen durch $3$ die Umkehrrechnung zum Malnehmen mit $3$ ist.
• Fertig: $x=6$.
• Mache doch schnell noch eine Probe: $3\cdot 6+6=18+6=24$ ✓

Mathematisch machst du dies so:

$\begin{array}{crclll} &3x+6&=&24&|&-6\\ \Leftrightarrow&3x&=&18&|&:3\\ \Leftrightarrow&x&=&6 \end{array}$

• Der Operationsstrich $|$ zeigt an, welche Äquivalenzumformung durchgeführt wird: „$-2$“ zum Beispiel bedeutet, dass auf beiden Seiten $2$ subtrahiert wird.
• Das Äquivalenzzeichen $\Leftrightarrow$ zeigt an, dass die Gleichung äquivalent umgeformt wurde. Was bedeutet das? Wenn die obere Gleichung für einen Wert eine wahre Aussage darstellt, dann ist dies auch für die untere der Fall. Dies gilt ebenso umgekehrt.

Gleichungen umstellen

Wir schauen uns jetzt noch weitere Beispiele zum Umstellen von Gleichungen an.

Beispiel 1

Du sollst die lineare Gleichung lösen: $4x-2=x+4$

• Addiere erst einmal auf beiden Seiten $2$: So erhältst du $4x=x+6$.
• Nun kannst du auf beiden Seiten $x$ subtrahieren: $3x=6$.
• Fast fertig: Du musst noch durch $3$ dividieren und erhältst so die Lösung $x=2$.
• Probe: $4\cdot 2-2=8-2=6=2+4$ ✓

Beispiel 2

In diesem Beispiel musst du noch einige Termumformungen durchführen: $4(x+1)+3=7(x-1)+2$.

• Wende auf beiden Seiten das Distributivgesetz an: $4x+4+3=7x-7+2$.
• Fasse nun die Zahlen zusammen: $4x+7=7x-5$.
• Nun kannst du $7$ subtrahieren: $4x=7x-12$.
• ... und $7x$ subtrahieren: $-3x=-12$.
• Dividiere noch durch $-3$. So kommst du zu der Lösung $x=4$.
• Führe doch einmal auf einem Blatt Papier die Probe durch.

Beispiel 3

In diesem Beispiel sollst du noch einmal die mathematische Schreibweise mit dem Äquivalenzzeichen und dem Operationsstrich üben. „$T$“ steht für „Termumformung“. Gelöst werden soll die Gleichung

$x^2+3(x+2)-4(x+3)=(x+1)\cdot(x-1)+x-1$.

In dieser Aufgabe wird die dritte binomische Formel $(x+1)\cdot (x-1)=x^2-1$ verwendet:

$\begin{array}{crclll} &x^2+3(x+2)-4(x+3)&=&(x+1)\cdot(x-1)+x-1&|&T\\ \Leftrightarrow&x^2+3x+6-4x-12&=&x^2-1+x-1&|&T\\ \Leftrightarrow&x^2-x-6&=&x^2+x-2&|&-x^2\\ \Leftrightarrow&-x-6&=&x-2&|&+6\\ \Leftrightarrow&-x&=&x+4&|&-x\\ \Leftrightarrow&-2x&=&4&|&:(-2)\\ \Leftrightarrow&x&=&-2 \end{array}$