Übergangsmatrizen
Einige Prozesse können mit Hilfe von Matrizen dargestellt werden: Ein Bestand, also Vektor, zu einem späteren Zeitpunkt ergibt sich als Produkt einer Matrix mit dem Bestand, ebenfalls als Vektor, jetzt. Diese Matrix wird als Übergangsmatrix bezeichnet.
Inhaltsverzeichnis zum Thema
- Was ist ein Übergangsdiagramm?
- Erstellung einer Übergangsmatrix aus einem Übergangsdiagramm
- Eigenschaften der Übergangsmatrix
Was ist ein Übergangsdiagramm?
zur Einführung ein Beispiel aus dem täglichen Leben an. In einer Gegend befinden sich drei Supermärkte A, B und C. Das folgende Übergangsdiagramm zeigt die Bewegungen der Kunden zwischen diesen drei Supermärkten an:
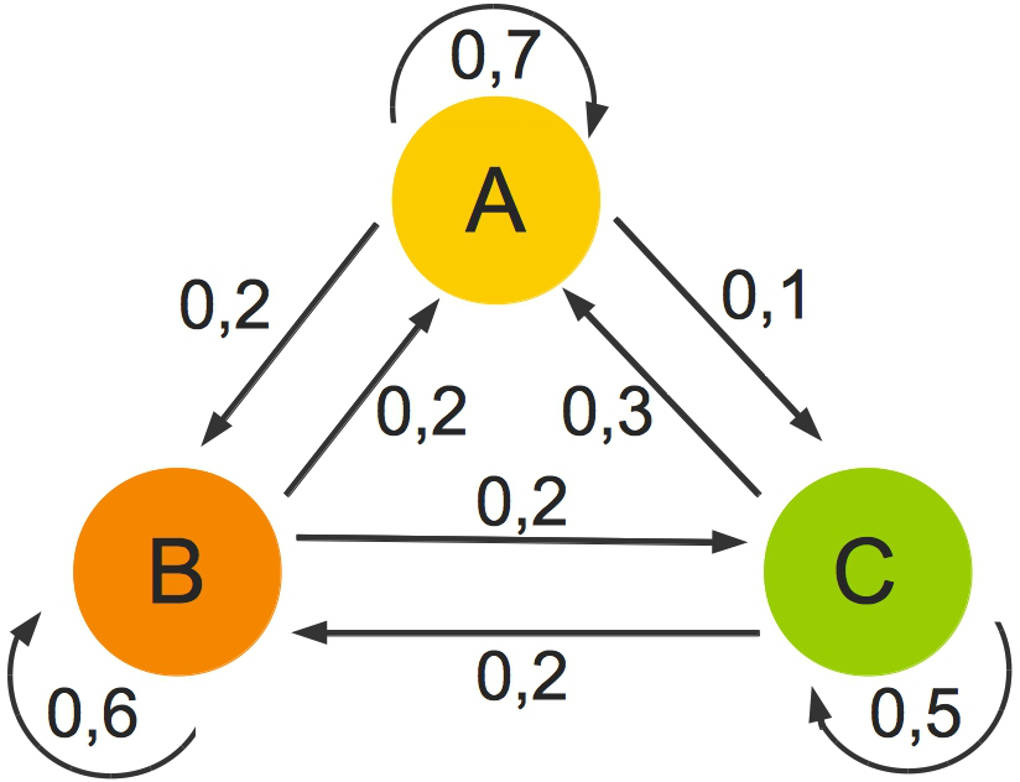
Was bedeutet dies? Schauen dir einmal den Supermarkt A an:
- Ein Pfeil führt von A zu sich selbst. Dieser ist mit beschriftet. Das bedeutet, dass der Kunden von Supermarkt A diesem auch treu bleiben.
- Ein Pfeil führt von A nach B. An diesem steht . Dies bedeutet, dass der Kunden von Supermarkt A zu Supermarkt B abwandern.
- Ebenso siehst du, dass die verbleibenden der Kunden von Supermarkt A zu Supermarkt C abwandern.
Die weiteren Bewegungen kannst du analog ablesen.
Erstellung einer Übergangsmatrix aus einem Übergangsdiagramm
Die Kundenbewegungen lassen sich auch in der Form darstellen. Dabei ist:
- die Matrix, welche die Übergänge beschreibt. Diese wird als Übergangsmatrix bezeichnet.
- der Vektor, welcher die aktuellen Zahlen der Kunden der drei Supermärkte enthält.
Die Übergangsmatrix kannst du spaltenweise aufschreiben:
- Die erste Spalte zeigt die Bewegung von Supermarkt A zu den jeweiligen Supermärkten A, B und C an.
- Die zweite Spalte entspricht dann den Bewegung von Supermarkt B zu den jeweiligen Supermärkten A, B und C an. Und die dritte Spalte entspricht der Kundenbewegung von Supermarkt C.
Daraus ergibt sich folgende Matrix:
- Werden nun die einzelnen Einträge einer Spalte addiert, ergibt sich in allen drei Spalten die Summe 1.
- Zum Beispiel zeigt die zweite Spalte die Bewegung von Supermarkt B zu A, B und C an. Addierst du nun die zugehörigen Einträge des 2. Spalt, ergibt sich: .
Anwendungsbeispiel für Übergangsmatrizen
Insgesamt Kunden verteilen sich zu Beginn der Beobachtung wie folgt auf die drei Supermärkte: * Supermarkt A * Supermarkt B * C jeweils
Somit ergibt sich folgender Vektor:
Möchtest du nun wissen, wie viele Kunden in dem jeweiligen Supermarkt nach einer Periode einkaufen, multiplizierst du die Matrix mit dem Vektor . Die Kundenbewegung für die einzelnen Supermärkte lassen sich mittels Übergangsmatrix bestimmen . Hierfür multiplizierst du jede Zeile der Matrix mit dem Vektor:
Das bedeutet, dass nach einer Periode Kunden bei A, bei B und bei C einkaufen. Du siehst, es sind immer noch Kunden. Dies liegt daran, dass die Spaltensummen immer ergeben. In diesem Modell wird davon ausgegangen, dass jeder Kunde weiterhin bei einem der 3 Supermärkte einkauft.
Ebenso kannst du berechnen, wie die Kunden sich nach oder Perioden auf die Supermärkte verteilen.
Du kannst umgekehrt auch herausfinden, wie die Kunden sich vor einer Periode auf die Supermärkte verteilt haben. Dabei musst du die Gleichung lösen.
Eigenschaften der Übergangsmatrix
Du hast bereits gesehen, dass die Summen der Spaltenelemente der obigen Matrix immer ergibt. Dies ist nicht immer so.
Definitionen
Alle Einträge einer Übergangsmatrix sind Zahlen zwischen und :
- Eine Übergangsmatrix heißt zeilenstochastisch, wenn die Summe der Zeilenelemente immer ergibt.
- Eine Übergangsmatrix heißt spaltenstochastisch, wenn die Summe der Spaltenelemente immer ergibt.
- Eine Übergangsmatrix heißt doppelt-stochastisch, wenn sie gleichzeitig zeilen- und spaltenstochastisch ist.
Übergangsmatrizen sind quadratische Matrix. In dem obigen Beispiel ist eine -Matrix, deren Einträge alle zwischen und liegen, gegeben. Eine Übergangsmatrix ist immer entweder spalten- oder zeilenstochastisch.
Woher kennst du dies, dass Werte zwischen und liegen? Du könntest es von Wahrscheinlichkeiten kennen. Häufig werden mit Übergangsmatrizen in der Wahrscheinlichkeitstheorie Übergangswahrscheinlichkeiten ausgedrückt.
Alle Videos zum Thema
Videos zum Thema
Übergangsmatrizen (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Übergangsmatrizen (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen





 Übergangsmatrizen – Beispiel Supermarkt
Übergangsmatrizen – Beispiel Supermarkt
 Übergangsmatrizen – Beispiel Wanderbewegungen
Übergangsmatrizen – Beispiel Wanderbewegungen












