Geometrische Formen, Muster und Reihen

Inhaltsverzeichnis zum Thema

• Einführung
• Was ist eine Fläche?
• Ausblick: Was ist ein Körper?
• Dreiecke
• Vierecke
• Kreise
• Ausblick
• Was sind Muster?
• Spiegeln und Symmetrie
• Flächen selbst zeichnen
• Parkettieren

Einführung

Schau dich einmal etwas in deinem Zuhause um. Überall kannst du Dinge sehen. Diese haben verschiedene Formen. Auch in der Mathematik lernst du, was Formen sind. Einige davon hast du ganz sicher bereits gesehen. Wir schauen uns im Folgenden Flächen an. Weißt du schon, was eine Fläche ist?

Was ist eine Fläche?

Um die Geometrie und Formen richtig zu verstehen, musst du wissen, was eine Fläche ist. Die Fläche einer ebenen Figur fasst alle Punkte zusammen, die sich im Inneren sowie auf dem Rand einer Figur befinden. Puh, das hört sich ganz schön kompliziert an.

Für ein Grundverständnis geht das auch einfacher: In dem Wort Fläche steckt das Wort flach. Eine Fläche ist also flach. Das unterscheidet eine Fläche von einem Körper.

Ausblick: Was ist ein Körper?

Ein Körper ist etwas, das du umfassen kannst. Zum Beispiel ist der menschliche Körper ein Körper. Du kannst ja deine Mama umarmen. Das geht mit einer Fläche nicht. Mathematische Körper sind Würfel wie der Spielwürfel, oder Kugeln wie ein Fußball. Es gibt noch sehr viel mehr Körper. Die lernst du sicher auch noch kennen.

Dreiecke

Hast du schon einmal ein solches Verkehrsschild gesehen?

Es zeigt einen Bauarbeiter. Damit wird auf eine Baustelle hingewiesen. Aber darum geht es hier ja nicht. Das Schild hat die Form eines Dreiecks.

Dreiecke, das merkst du schon an dem Namen, haben drei Ecken. Sie haben auch drei Seiten sowie drei Winkel.

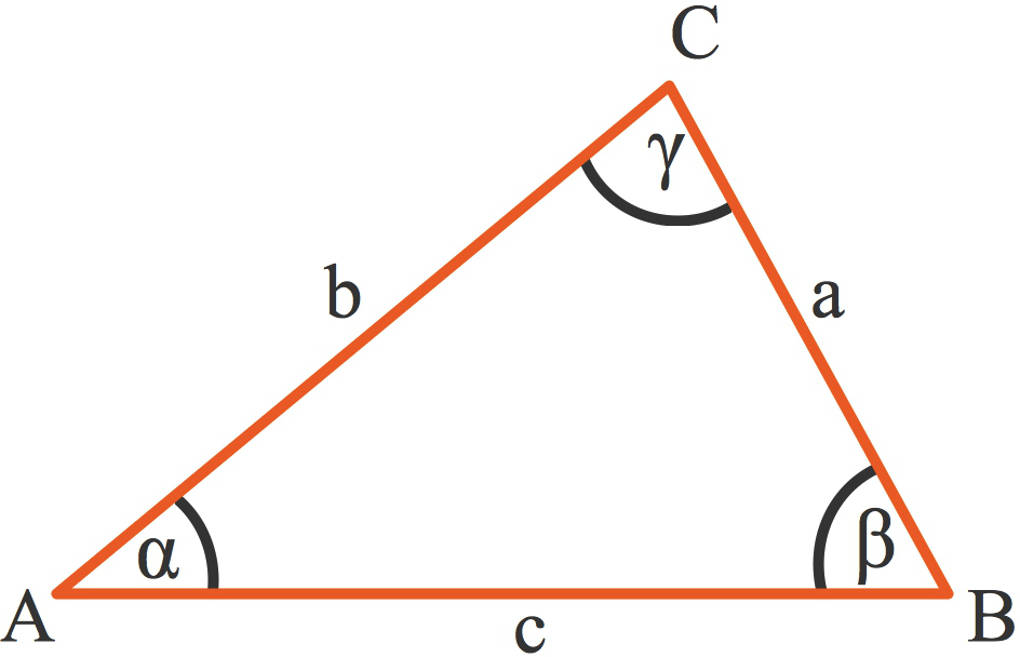
• Es gibt Dreiecke, bei denen zwei Seiten gleich lang sind: Das sind gleichschenklige Dreiecke.
• Manche Dreiecke haben drei gleich lange Seiten. Hierbei handelt es sich um gleichseitige Dreiecke. Übrigens: Bei gleichseitigen Dreiecken sind auch alle Winkel gleich groß, nämlich $60^{\circ}$.
• Wenn ein Dreieck einen rechten Winkel hat, nennt man es rechtwinklig. Was ist nochmal ein rechter Winkel? Richtig: Ein $90^{\circ}$-Winkel wird als rechter Winkel bezeichnet.

Vierecke

Wie viele Ecken hat wohl ein Viereck? Genau: vier. Ein Viereck hat auch vier Seiten und vier Winkel.

Hier siehst du ein allgemeines Viereck.

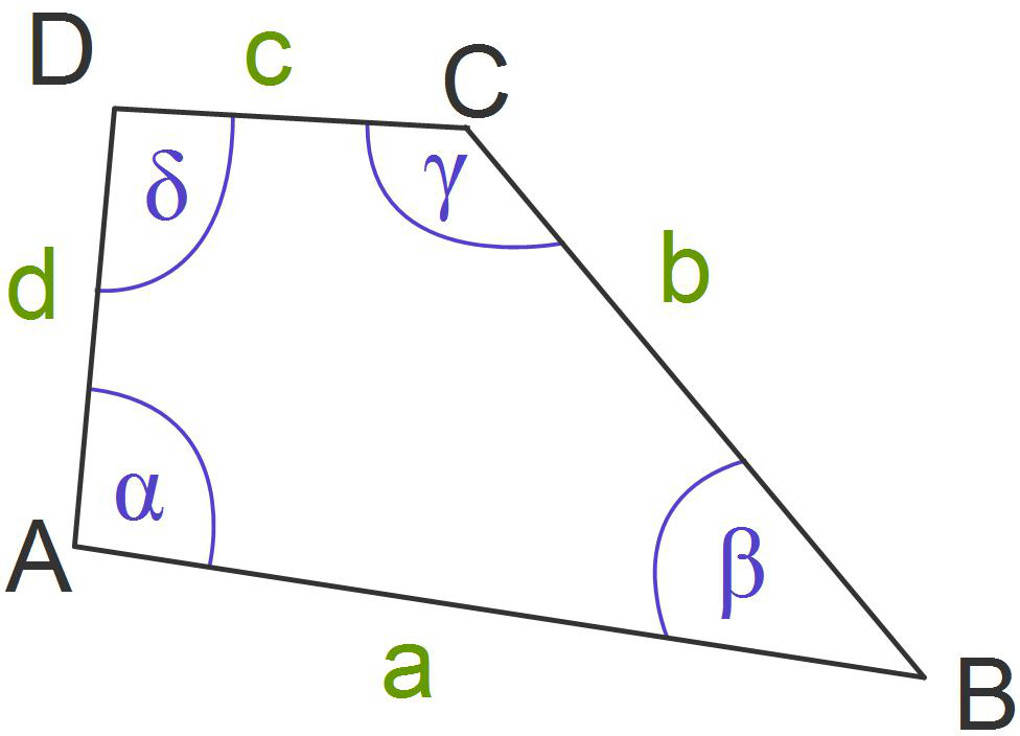
Nun gibt es noch verschiedene spezielle Vierecke. Einen Überblick erhältst du im Haus der Vierecke:

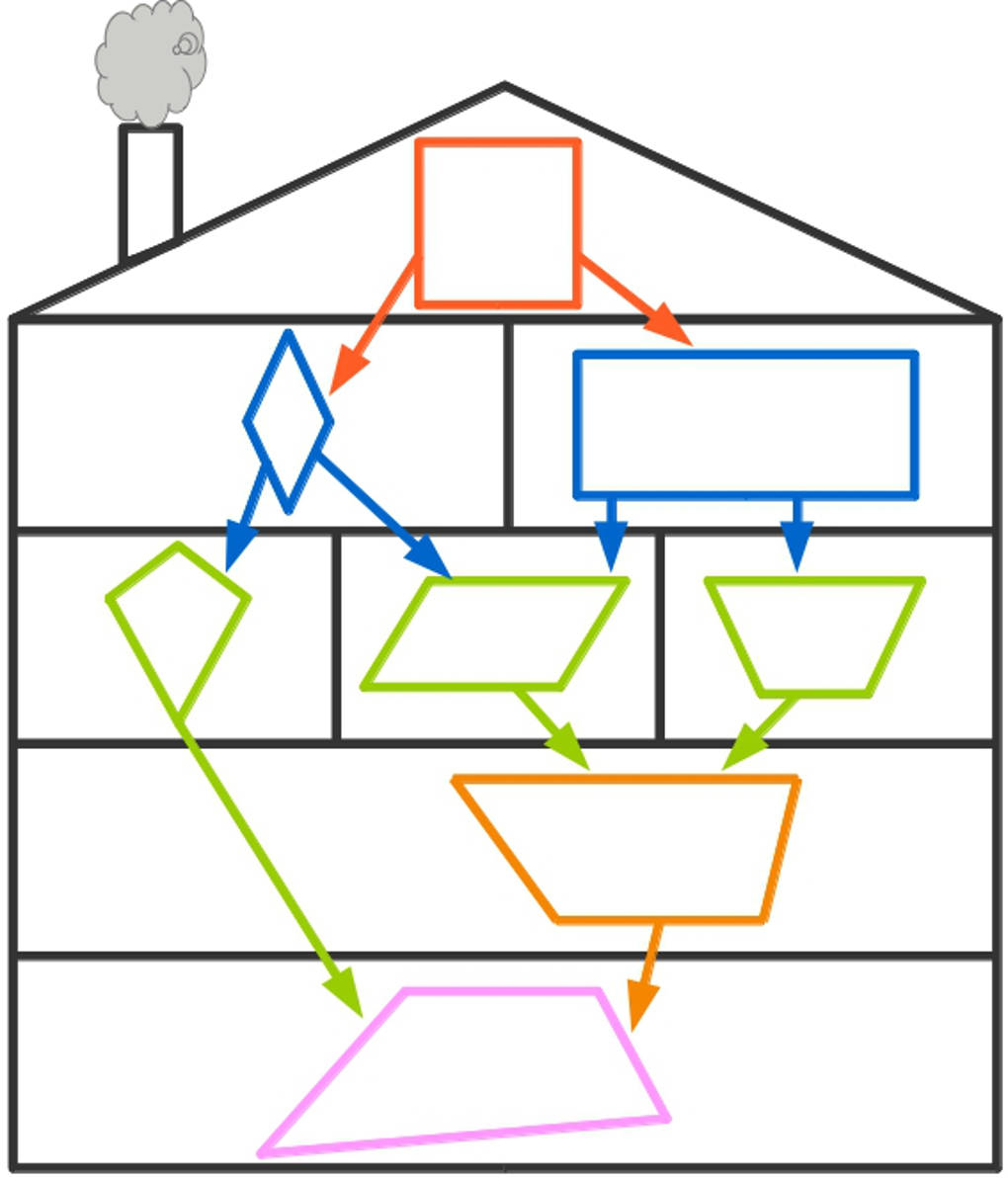
Zwei der abgebildeten Vierecke schauen wir uns noch ein wenig genauer an:

• Ganz oben wohnt das Quadrat: Bei einem Quadrat sind alle vier Seiten gleich lang und paarweise parallel zueinander. Alle Winkel sind rechte Winkel.
• Rechts unter dem Quadrat wohnt das Rechteck: Bei einem Rechteck sind ebenfalls alle Winkel rechte Winkel. Daher kommt der Name. Die einander gegenüberliegenden Seiten sind gleich lang und parallel zueinander. Es müssen allerdings nicht alle Seiten gleich lang sein. Wenn du dir dein Mathebuch von oben anschaust, siehst du ein Rechteck. Auf diesem steht zum Beispiel Mathematik 3. Klasse und vielleicht sind verschiedene Flächen darauf abgebildet.
• Merke dir: Jedes Quadrat ist sicher auch ein Rechteck. Allerdings ist nicht jedes Rechteck ein Quadrat.

Kreise

Kommen wir noch einmal zu einem Verkehrsschild. Vielleicht hast du dieses auch schon einmal gesehen:

Dieses Schild zeigt an, dass man auf den Gegenverkehr achten muss. Dieses Schild ist nicht dreieckig. Es ist rund. Die Form dieses Schildes wird als Kreis bezeichnet.

Ein Kreis hat einen Mittelpunkt $M$ und einen Radius $r$. Manchmal betrachtet man auch den Durchmesser $d$ eines Kreises. Das ist der doppelte Radius.

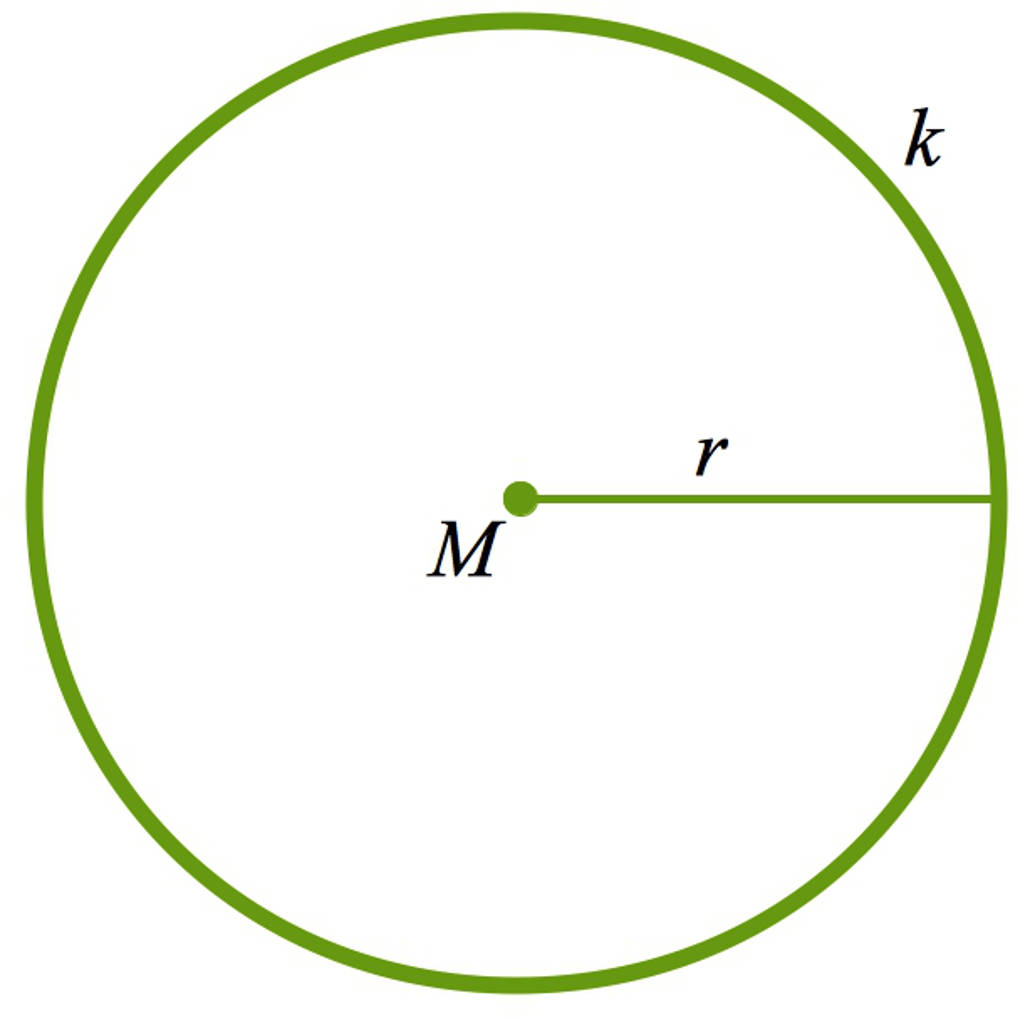
Ausblick

Du kannst mit Formen auch Muster legen wie zum Beispiel Mandalas. Im Folgenden ist ein Muster dargestellt, das sich aus mehreren gleichschenkligen Dreiecken und einem Quadrat zusammensetzt.

Wenn du Formen spiegelst oder bewegst, erhältst du ebenfalls verschiedene Muster.

Was sind Muster?

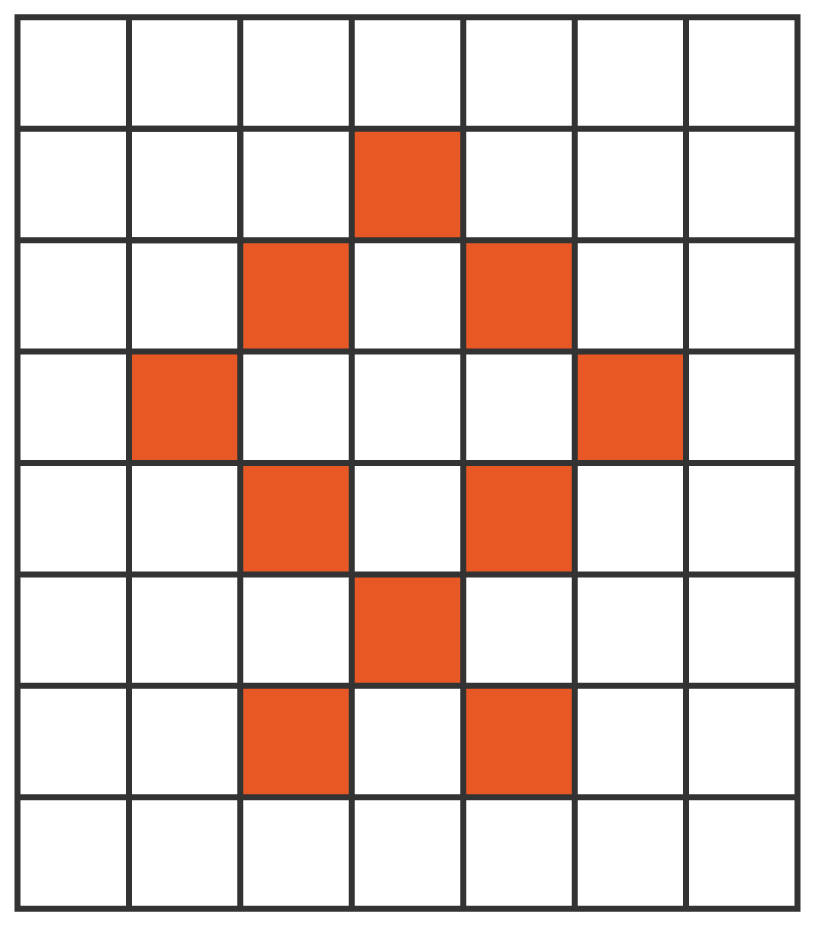
Kennst du Mandalas? Das sind Muster in einem Kreis. Ein Muster nennt man eine regelmäßige Anordnung von Formen oder Zeichen. Sie wiederholen sich immer wieder, zum Beispiel Herz – Herz – Herz - Blitz, Herz – Herz - Herz - Blitz, Herz - … Siehst du, wo das Muster anfängt und wo es aufhört? Prima, dann kannst du es sogar selbst fortführen. In der Mathematik gibt es geometrische Muster. Einige werden nur mit dem Zirkel erstellt und sehen ähnlich aus wie ein begonnenes Mandala. In einem Muster sind alle Elemente in gleicher Weise geordnet und sie wiederholen sich. Muster kannst du selbst vervollständigen. Schau dir einmal das Bild unten an. Dieses Muster mit Kästchen hat sechs Reihen. In der siebten Reihe fehlen nun zwei Kästchen. Wo müssen sie ergänzt werden?

Spiegeln und Symmetrie

Du kannst selbst ein Bild verändern. Male mit Wasserfarben auf ein Blatt Papier. Falte es nun in der Mitte. Klappe es vorsichtig wieder auf. Wie wurde das Bild durch das Falten verändert? Es wurde verdoppelt! Es ist an deiner Faltlinie gespiegelt worden. Das bedeutet, auf beiden Seiten erhältst du das gleiche Bild. Auf die Faltlinie kannst du auch einen Spiegel stellen. Wenn du hineinschaust, sieht dein Bild ganz genauso aus. Es ist wieder auf beiden Seiten gleich. Die Faltlinie nennt man Spiegelachse. Mithilfe dieser kannst du auch selbst ein Spiegelbild zeichnen. Links der Spiegelachse muss alles genauso groß und genauso weit voneinander entfernt sein wie rechts. Das nennt man dann Symmetrie.

Flächen selbst zeichnen

Weißt du schon, was Flächen sind? Alle Flächen haben gemeinsam, dass sie flach sind. Es gibt viele verschiedene, wie zum Beispiel das Rechteck. Das Rechteck hat vier Ecken und die beiden gegenüberliegenden Seiten sind jeweils gleich lang. Auch ein Quadrat hat vier Ecken, es sind jedoch alle vier Seiten gleich lang. Das Dreieck hingegen hat nur drei Ecken. Ein Kreis hat überhaupt keine Ecken und ist daher rund. Mit kariertem Papier, einem Stift und einem Lineal kannst du selbst Flächenformen gestalten. Überlege vorher, wie deine Fläche aussehen soll. Was musst du dabei beachten? Zeichne zuerst Punkte für die Ecken auf das Papier. Verbinde sie nun mit Hilfe eines Lineals. Einen Kreis zeichnest du am besten mit einem Zirkel. Auch um ein umgedrehtes Glas herum kannst du einen Kreis zeichnen. Jetzt kannst du solche Flächenformen auf deinem Papier noch regelmäßig anordnen. So entstehen tolle Muster!

Parkettieren

Einige Formen oder Muster kannst du auch immer wieder direkt aneinander zeichnen. Das kennst du vielleicht von den Steinen vor dem Haus, den Fliesen in eurem Badezimmer oder vom Parkett auf dem Fußboden. Das ist ein Fußbodenbelag aus kleinen Hölzern, die im immer gleichen Muster auf dem Boden verlegt sind. Besonders in alten Villen oder Schlössern ist das sehr aufwändig gemacht. Es dürfen keine Lücken im Muster entstehen. Die Formen dürfen sich auch nicht überlappen. Eine ganze Fläche aus diesen regelmäßigen Mustern nennt man Parkettierung. Auf dem Bild unten siehst du eine Parkettierung.

Welche Formen gibt es? Wie sind sie angeordnet? Werden sie verändert? Kannst du das Muster im Bild erkennen? Dann kannst du das Parkettmuster jetzt vervollständigen. Mit Lili und Niko machen Muster dir bestimmt großen Spaß!