Grundlagen zu Wachstum

Inhaltsverzeichnis zum Thema

• Einführung: Wachstum
• Wachstum am Beispiel deines Taschengeldes
• Darstellung von Wachstum
• Wachstum rekursive Darstellung
• Wachstum Darstellung in einer Wertetabelle
• Wachstum explizite Darstellung
• Verschiedene Wachstumsmodelle
• Lineares Wachstum
• Quadratisches Wachstum
• Prozentuales Wachstum
• Exponentielles Wachstum

Einführung: Wachstum

Wachstum bedeutet in der Mathematik die Zunahme oder auch Vergrößerung einer Größe in Abhängigkeit von der Zeit.

Es existiert auch negatives Wachstum, also die Abnahme einer Größe in Abhängigkeit der Zeit.

Wachstum am Beispiel deines Taschengeldes

Du bekommst $30~€$ Taschengeld pro Monat. Jedes Jahr erhältst du $5~€$ mehr Taschengeld. Du siehst, dein Taschengeld wächst von Jahr zu Jahr an.

Darstellung von Wachstum

Schau dir noch einmal das Beispiel mit dem Taschengeld an. Du kannst die Entwicklung des Taschengeldes auf verschiedene Arten darstellen.

Wachstum rekursive Darstellung

Jetzt mit $15$ Jahren, also $t=0$, erhältst du $N_0=N(0)=30~€$ Taschengeld.

• In ersten Jahr erhältst du pro Monat $30~€+5~€=35~€$ Taschengeld.
• In zwei Jahren erhältst du $35~€+5~€=40~€$ Taschengeld pro Monat.
• Nach $t$ Jahren erhältst du $N(t)$ Taschengeld und ein Jahr später $5~€$ mehr, also $N(t+1)=N(t)+5~€$.

Eine solche Darstellung wird rekursiv genannt. Der Nachteil dieser rekursiven Darstellung besteht darin, dass du immer die ersten $t$ Werte von $N(t)$ berechnen musst, um den folgenden zu berechnen.

Wachstum Darstellung in einer Wertetabelle

Das Wachstum einer Funktion kannst du in einer Wertetabelle darstellen. Diese Angaben kannst du in einer Wertetabelle aufschreiben.

Wachstum explizite Darstellung

Um das Problem mit der Berechnung der ersten $t$ Werte für $N(t)$ zu umgehen, kannst du dieses auch explizit darstellen. Da dein Taschengeld jedes Jahr um $5~€$ erhöht wird, kannst du dies auch so schreiben: $N(t)=30~€+t\cdot 5~€$.

Zum Beispiel ist $N(4)=30~€+4\cdot 5~€=30~€+20~€=50~€$.

Das Wachstum, welches am Beispiel deines Taschengeldes beschrieben wird, wird als lineares Wachstum bezeichnet. Es gibt noch verschiedene andere Wachstumsmodelle.

Verschiedene Wachstumsmodelle

Wir schauen uns nun im Folgenden verschiedene Wachstumsmodelle an. Es seien

• $N_0=N(0)$ der Anfangsbestand, der Bestand zum Zeitpunkt $0$ oder Beobachtungsbeginn.
• $N(t)$ ist der Bestand zum Zeitpunkt $t$. Dabei gilt $t\ge 0$.

Lineares Wachstum

Lineares Wachstum liegt vor, wenn die Änderung $D$ des Wertes $N(t)$ in gleichen Zeitabständen immer gleich groß ist. Der Wert $N(t)$ ändert sich also proportional zum Argument $t$.

Ebenso ist lineare Abnahme dann gegeben, wenn der Wert $N(t)$ in gleichen Zeitabständen immer um den gleichen Betrag abnimmt.

Die Wachstumsfunktion $N$ ist dann explizit gegeben durch $N(t)=N(0)+t\cdot D$.

Quadratisches Wachstum

Quadratisches Wachstum oder auch quadratische Abnahme liegt vor, wenn du die Änderung des Bestandes $N(t)$ mit einer Funktionsgleichung für quadratische Funktionen dargestellt werden kann $N(t)=at^2+bt+c$ mit $ a ~\neq 0$. Dabei liegt für positive $a$ Wachstum vor und für negatives $a$ Abnahme.

Ein Beispiel für quadratisches Wachstum ist der im freien Fall zurückgelegte Weg $s(t)$ in Metern in $t$ Sekunden. Es ist $s(t)=5t^2$.

Prozentuales Wachstum

Prozentuales Wachstum ist die Zunahme einer Größe innerhalb eines bestimmten Zeitraums, ausgedrückt in Prozent.

Hierzu kennst du bereits ein Beispiel aus der Zinsrechnung. Du hast Geld auf einem Sparbuch angelegt. Jährlich kommen $p~\%=5~\%$ Zinsen hinzu. Dieser prozentuale Zuwachs wird als Wachstumsrate bezeichnet. Der Wachstumsfaktor ist $a=1+\frac{5}{100}=1,05>1$.

Du kannst nun das Wachstum wie folgt angeben $N(t)=N_0\cdot a^t$.

Auch hier kannst du prozentuale Abnahme erklären. Dann ist $a=1-\frac{p}{100}<1$.

Exponentielles Wachstum

Du siehst bereits bei dem vorherigen Beispiel zum prozentualen Wachstum, dass die unabhängige Variable $t$ im Exponenten steht.

Dies ist bereits ein Beispiel für exponentielles Wachstum. Dabei ändert sich der Bestand $N(t)$ in gleichen Zeitabständen immer um denselben Faktor.

Exponentielles Wachstum kann mit folgender Funktionsgleichung beschrieben werden $N(t)=N_0\cdot a^t$.

Diese Funktionsgleichung kannst du auch mit der Euler'schen Zahl $e=2,71828...$ als Basis schreiben. Verwende hierfür:

$a^t=e^{\ln(a^t)}=e^{\ln(a)\cdot t}$.

Du erhältst damit $N(t)=N_0\cdot e^{\ln(a)\cdot t}$. Der Faktor $\ln(a)$ wird als Wachstumskonstante bezeichnet.

Hier siehst du einen Überblick über die vorgestellten Wachstumsmodelle:

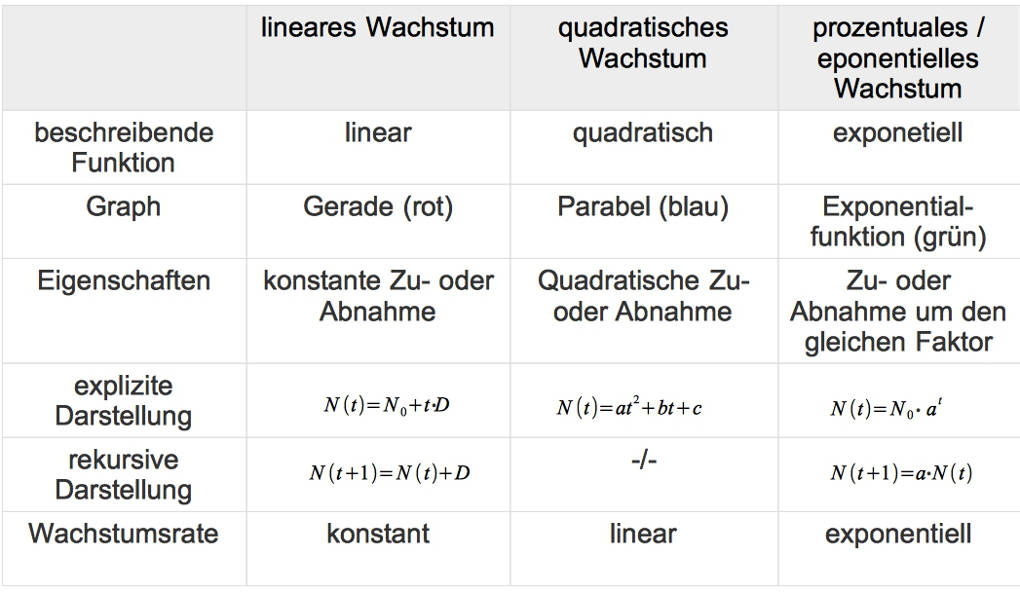
Die zugehörigen Graphen zu dem jeweiligen Wachstum sind in der folgenden Grafik dargestellt:

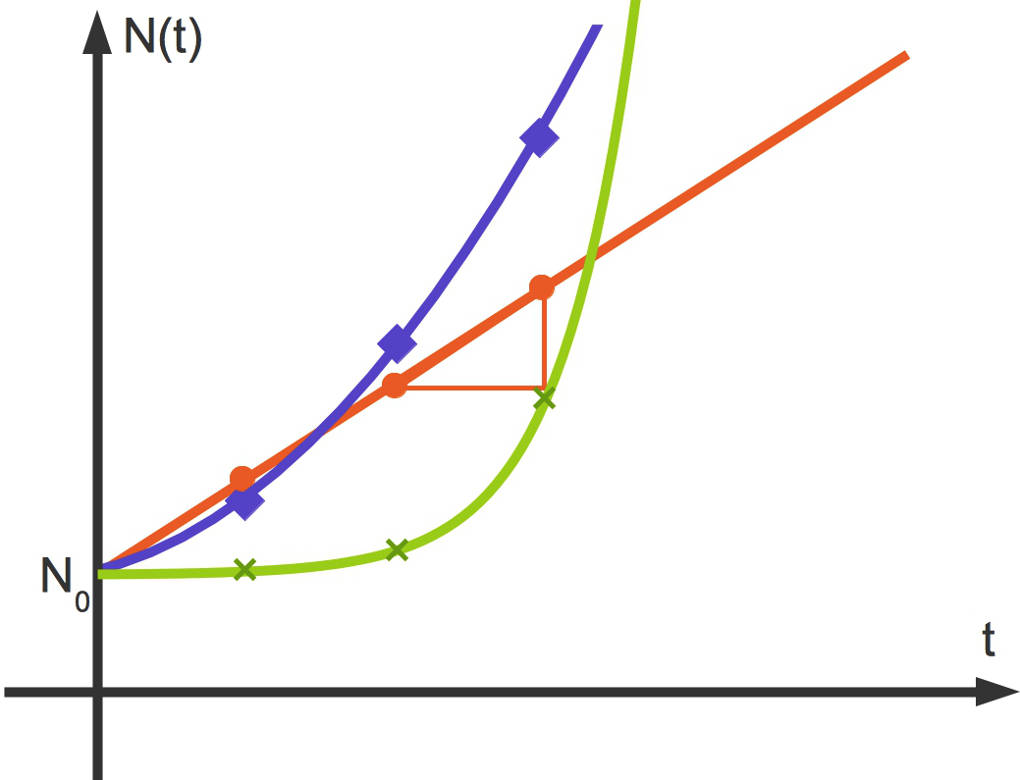
• Die rote Gerade stellt lineares Wachstum dar. Das abgebildete Dreieck entspricht einem Steigungsdreieck. An diesem kannst du die konstante Änderung erkennen.
• Die blaue Parabel stellt quadratisches Wachstum dar.
• Der grüne Funktionsgraph gehört zu exponentiellem Wachstum.