Partielle Ableitungen und Tangentialebene

Inhaltsverzeichnis zum Thema

• Funktionen mit mehreren Veränderlichen
• Was ist eine partielle Ableitung?
• Die partiellen Ableitungen erster Ordnung
• Die partiellen Ableitungen zweiter Ordnung
• Anwendungen der partiellen Ableitung
• Tangentialebene in einem Punkt
• Die notwendige Bedingung bei Extrema
• Die Kettenregel bei Funktionen mit mehreren Veränderlichen

Funktionen mit mehreren Veränderlichen

Du kennst bereits Funktionen mit einer Veränderlichen, zum Beispiel $f(x)=x^2$.

Bei Funktionen mit mehreren Veränderlichen hängt die Funktion nicht nur von einer Variablen $x$ ab, sondern von mehreren: $x$, $y$ und $z$ oder – ganz allgemein – von $x_1$, $x_2$, ... Wir schreiben dann eine Funktion $f$ folgendermaßen:

$f(x_1;x_2;...;x_n)$.

Im Folgenden schauen wir uns Beispiele zu Funktionen mit zwei Veränderlichen an. Alles, was wir hier lernen, lässt sich analog auch auf mehr als zwei Veränderliche anwenden.

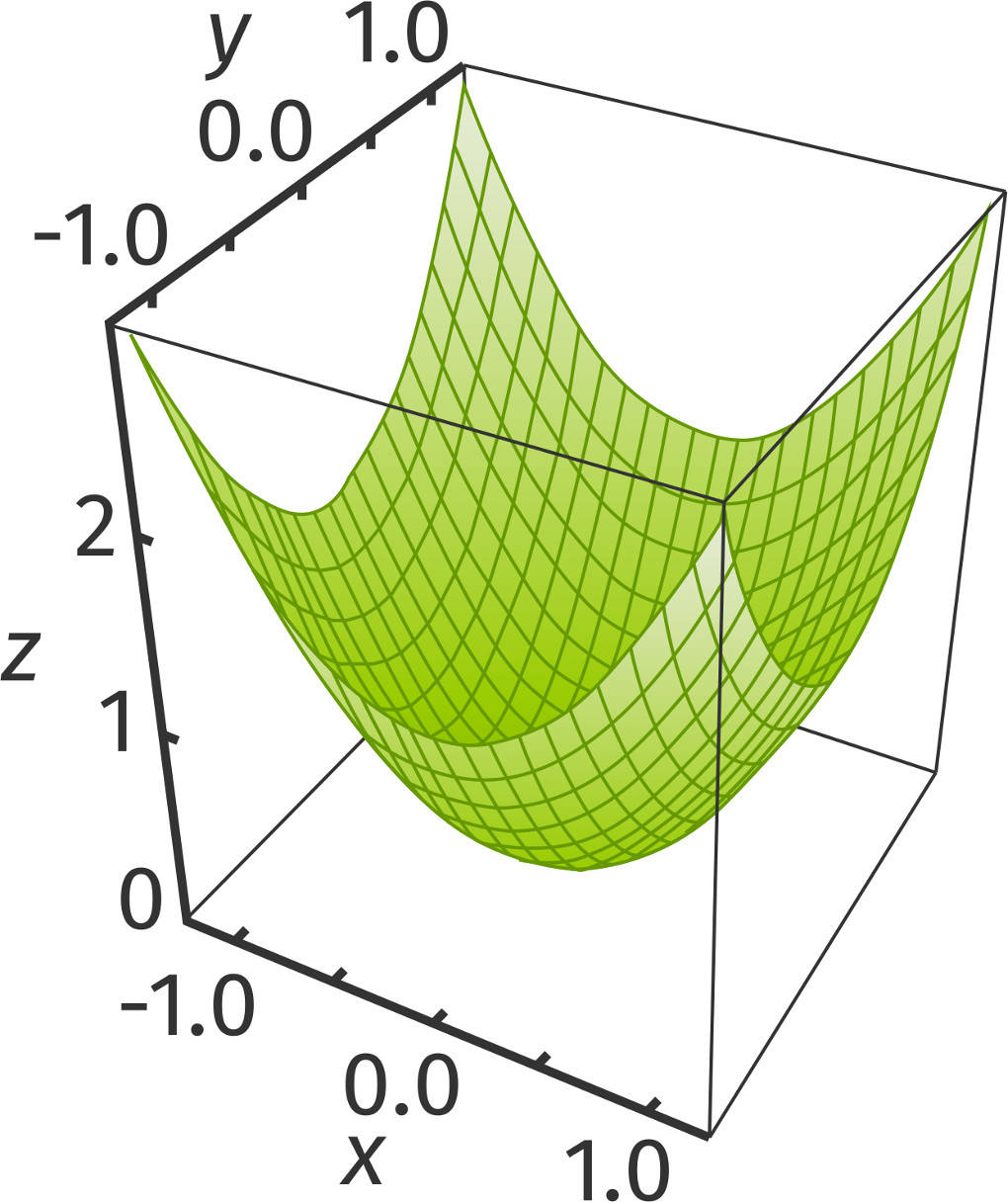
Beginnen wir mit der Funktion $f(x;y)=x^2+y^2$.

Der Funktionsgraph dieser Funktion ist eine Fläche im Raum und wird als Paraboloid bezeichnet. Dies kannst du dir wie eine 3D-Parabel vorstellen.

Was ist eine partielle Ableitung?

Wenn du bei der Funktion $f(x;y)=x^2+y^2$ mit $y=y_0$ eine Veränderliche festhältst, erhältst du eine Funktion $h(x)=f(x;y_0)=x^2+y_0^2$ in einer Veränderlichen. Deren Ableitung ist $h'(x)=2x$.

Du kannst dir also eine partielle Ableitung so vorstellen: Du leitest die Funktion jeweils nach einer der beiden Veränderlichen ab und betrachtest dabei die andere Veränderliche als Konstante.

Die partiellen Ableitungen erster Ordnung

Die partiellen Ableitungen erster Ordnung werden so aufgeschrieben:

• $\frac{\partial f}{\partial x}=f_x$ ist die partielle Ableitung erster Ordnung nach $x$.
• $\frac{\partial f}{\partial y}=f_y$ ist die partielle Ableitung erster Ordnung nach $y$.

Häufiger werden die abkürzenden Schreibweisen $f_x$ sowie $f_y$ verwendet.

Man kann die partiellen Ableitungen erster Ordnung auch als Vektor schreiben. Dieser wird als Gradient bezeichnet:

$\nabla f=\begin{pmatrix} \frac{\partial f}{\partial x}\\ \frac{\partial f}{\partial y} \end{pmatrix}=\begin{pmatrix} f_x \\ f_y \end{pmatrix}$.

Bei dem obigen Beispiel $f(x)=x^2+y^2$ ist somit $f_x=2x$ und $f_y=2y$.

Schauen wir uns mit der Funktion $g(x)=2\sin(x)\cdot y-3x\cdot y^2$ ein weiteres Beispiel an. Die partiellen Ableitungen lauten:

• $g_x=2\cos(x)\cdot y-3y^2$ und
• $g_y=2\sin(x)-6x\cdot y$.

Die partiellen Ableitungen zweiter Ordnung

Du kannst wie gewohnt auch Funktionen mit mehreren Veränderlichen mehrmals ableiten. Die partiellen Ableitungen zweiter Ordnung werden analog gebildet:

• $\frac{\partial^2 f}{\partial^2 x}=f_{xx}=2$,
• $\frac{\partial^2 f}{\partial x~\partial y}=f_{xy}=0$,
• $\frac{\partial^2 f}{\partial y~\partial x}=f_{yx}=0$ und
• $\frac{\partial^2 f}{\partial^2 y}=f_{yy}=2$.

Die partiellen Ableitungen zweiter Ordnung werden zusammengefasst zu der sogenannten Hesse-Matrix (hier in abkürzender Schreibweise):

$\text{H}_f=\begin{pmatrix} f_{xx}&f_{xy} \\ f_{yx}&f_{yy} \end{pmatrix}$.

Für die Funktion $f(x;y)=x^2+y^2$ ist die Hesse-Matrix hierdurch gegeben:

$\text{H}_f=\begin{pmatrix} 2&0 \\ 0&2 \end{pmatrix}$.

Anwendungen der partiellen Ableitung

Tangentialebene in einem Punkt

Bei Funktionen mit einer Veränderlichen kannst du mit Hilfe der ersten Ableitung an einer Stelle $x_0$ die Gleichung einer Tangente aufstellen.

Ähnlich funktioniert dies bei Funktionen mit mehreren Veränderlichen. Hier stellst du die Gleichung einer Tangentialebene auf.

Du benötigst die partiellen Ableitungen erster Ordnung. Wir schauen uns dies nochmals an dem Beispiel $f(x;y)=x^2+y^2$ an. Zunächst bestimmen wir den Berührpunkt. Dieser muss auf jeden Fall die Funktionsgleichung erfüllen: Für $x_0=1$ und $y_0=1$ ergibt sich $z_0=f(x_0;y_0)=1^2+1^2=2$. Der zu untersuchende Punkt hat also die Koordinaten $(1|1|2)$.

Eine Tangentialebene wird allgemein durch diese Gleichung beschrieben:

$z-z_0=f_x(x_0;y_0)(x-x_0)+f_y(x_0;y_0)(y-y_0)$.

Wir können unseren Punkt in diese Gleichung einsetzen:

• Dies führt zu der Gleichung $z-2=2(x-1)+2(y-1)$.
• Du kannst nun wie folgt umformen: $z-2=2x-2+2y-2$, also $z-2=2x+2y-4$.
• Diese Gleichung kannst du zu einer Ebenengleichung in Koordinatenform umstellen: $E:~2x+2y-z=2$.

Die notwendige Bedingung bei Extrema

Die notwendige Bedingung für Extrema bei Funktionen mit einer Veränderlichen lautet $f'(x)=0$. Bei Funktionen mit mehreren Veränderlichen muss der Gradient der Nullvektor sein. Das bedeutet, dass jede partielle Ableitung erster Ordnung gleich $0$ sein muss. Für $f(x)=x^2+y^2$ bedeutet dies:

• $f_x=2x=0$, also ist $x=0$.
• $f_y=2y=0$, also ist $y=0$.

Übrigens gilt als hinreichende Bedingung einer Hesse-Matrix, dass deren Determinante größer ist als $0$.

• Wenn $\text{H}_{1;1}$ positiv ist, liegt ein lokales Minimum vor,
• wenn $\text{H}_{1;1}$ negativ ist, liegt ein lokales Maximum vor und
• ansonsten ein Sattelpunkt.

Bei der Funktion $f(x;y)=x^2+y^2$ gelten folgende Eigenschaften:

• $\det(\text{H}_f)=4>0$ und
• $\text{H}_{1;1}=2>0$.

Es liegt also ein lokales Minimum vor, wie du auch an der abgebildeten Fläche erkennen kannst.

Die Kettenregel bei Funktionen mit mehreren Veränderlichen

Zu guter Letzt lernst du noch die Kettenregel für Funktionen mit mehreren Veränderlichen kennen. Sei $z=f(x(t);y(t))$ eine Funktion mit mehreren Veränderlichen. Die Veränderlichen sind $x$ und $y$, wobei sowohl $x=x(t)$ als auch $y=y(t)$ jeweils von der Veränderlichen $t$ abhängen.

Dann lässt sich $z$ wie folgt nach $t$ ableiten:

$z'(t)=\frac{\partial f}{\partial x}\cdot x'(t)+\frac{\partial f}{\partial y}\cdot y'(t)$.

Das erinnert dich sicher an die Kettenregel für Funktionen mit einer Veränderlichen.

• Hier sind $\frac{\partial f}{\partial x}$ und $\frac{\partial f}{\partial y}$ jeweils die Ableitungen der äußeren Funktionen.
• $x'(t)=\frac{dx}{dt}$ sowie $y'(t)=\frac{dy}{dt}$ sind die Ableitungen der inneren Funktionen.

Auch hier schauen wir uns wieder ein Beispiel an:

$z(t)=(x(t))^2+(y(t))^2=(t^2-2)^2+(2t+1)^2$.

Hier ist $x(t)=t^2-2$ und damit die erste Ableitung $x'(t)=2t$ sowie $y(t)=2t+1$ und die erste Ableitung $y'(t)=2$.

Nun kann die Kettenregel angewendet werden:

$\begin{array}{rcl} z'(t)&=&2x(t)\cdot 2t+2y(t)\cdot 2\\ &=&2(t^2-2)\cdot 2t+2(2t+1)\cdot 2\\ &=&4t^3-8t+8t+4\\ &=&4t^3+4. \end{array}$