Exponential- und e-Funktionen ableiten

Inhaltsverzeichnis zum Thema

• Ableitung von Exponentialfunktionen in der Lebenswelt
• Exponentialfunktionen
• Die natürliche Exponentialfunktion
• Die Ableitung der natürlichen Exponentialfunktion
• Die Ableitung einer allgemeinen Exponentialfunktion
• Eigenschaften der natürlichen Exponentialfunktion
• Beispiel 2
• Beispiel 3
• Beispiel 4

Ableitung von Exponentialfunktionen in der Lebenswelt

Auch Exponentialfunktionen kann man ableiten, doch wozu sollte man dies tun?

Betrachtet man beispielsweise die Ausbreitung einer Krankheit, bei der die Anzahl der Infizierten $N(t)$ zum Zeitpunkt $t$ durch die Funktion:

$N(t)=e^t$

beschrieben wird, wäre zur Einstufung der Bedrohungslage wichtig zu wissen, wie groß gerade die Momentangeschwindigkeit $v$ der Ausbreitung zum Zeitpunkt $t$ ist und und wie sich diese weiterentwickeln wird.

Hierzu würde man dann die obige Gleichung ableiten müssen, da die Momentangeschwindigkeit der Ausbreitung zum Zeitpunkt $t$:

$v(t)=(N(t))'$ ist.

Exponentialfunktionen

In Exponentialfunktionen steht die unabhängige Größe, die Variable im Exponenten.

Eine Exponentialfunktion hat die Form

$f(x)=a^x$ .

Dabei sind

• $x$ die Variable und
• $a\in \mathbb{R}$, $a\neq 0$, die Basis der Exponentialfunktion.

Üblicherweise schreibt man Exponentialfunktionen mit der Basis $e\approx2,71828$ der Euler'schen Zahl. Wie dies bei allgemeiner Basis gemacht wird, siehst du hier:

$f(x)=a^x=e^{\ln(a^x)}$,

da $e^{\ln(x)}=x$ ist. Nun wird die folgende Rechenregel für Logarithmen $\log(p^{q})=q\cdot \log( p)$ verwendet. Diese Regel gilt für jeden Logarithmus, unabhängig von der Basis. Damit ist

$f(x)=e^{\ln(a^x)}=e^{\ln(a)\cdot x}$.

Die natürliche Exponentialfunktion

Eine Exponentialfunktion mit der Basis $e$ wird als natürliche Exponentialfunktion bezeichnet

$f(x)=e^{x}$.

Die Ableitung der natürlichen Exponentialfunktion

Die Ableitung einer Funktion ist definiert mit Hilfe des Differentialquotienten als

$\begin{array}{rcl}f'(x)&=&\lim\limits_{h\to 0}\frac{f(x+h)-f(x)}h\\ &=&\lim\limits_{h\to 0}\frac{e^{x+h}-e^x}h\\ &=&\lim\limits_{h\to 0}\frac{e^x(e^h-1)}h\\ &=&e^x\cdot \lim\limits_{h\to 0}\frac{e^h-1}h=e^x \end{array}$

Die Euler'sche Zahl ist gerade so definiert, dass

$\lim\limits_{h\to 0}\frac{e^h-1}h=1$

ist. Damit ist $(e^x)'=e^x$.

Die Ableitung einer allgemeinen Exponentialfunktion

Mit Hilfe der Ableitung $(e^x)'=e^x$ kann jede Exponentialfunktion $f(x)=a^x$ mit der Basis $a\neq 0$ abgeleitet werden:

$\begin{array}{rcl}f'(x)&=&(a^x)'\\ &=&\left(e^{\ln(a)\cdot x}\right)'\\ &=&\ln(a)\cdot e^{\ln(a)\cdot x}\\ &=&\ln(a)\cdot a^x \end{array}$

Zur Ableitung von $ e^{\ln(a)\cdot x}$ wird die Kettenregel verwendet.

Eigenschaften der natürlichen Exponentialfunktion

Hier ist der Graph der natürlichen Exponentialfunktion $f(x)=e^x$ zu sehen.

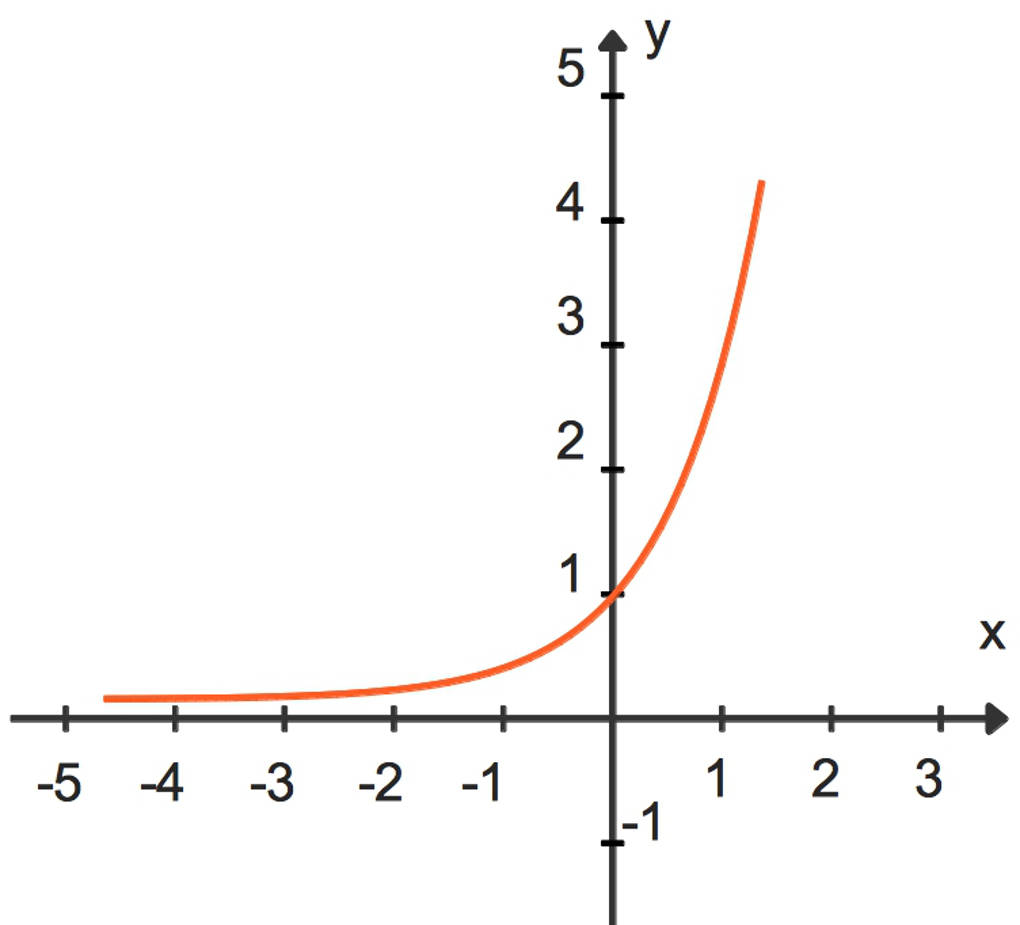
Die folgenden Eigenschaften sind in diesem Graphen zu erkennen:

• $e^x>0$ und insbesondere ist $e^x\neq 0$
• $\lim\limits_{x\to \infty} e^x=$„$\infty$“
• $\lim\limits_{x\to -\infty} e^x=0$

Darüber hinaus ist es sinnvoll, dass du dir einige spezielle Funktionswerte einprägst:

• $e^0=1$ Dies ist der y-Achsenabschnitt des Graphen.
• $e^1=e\approx 2,71828$

Der Graph der Funktion $f(x)=a^x$ für $a>1$ verläuft so ähnlich wie der abgebildete Graph. Ebenso gelten die Eigenschaften

• $a^x>0$ und insbesondere ist $a^x\neq 0$
• $\lim\limits_{x\to \infty} a^x=$„$\infty$“
• $\lim\limits_{x\to -\infty} a^x=0$
• $a^0=1$
• $a^1=a$

Wenn für die Basis $0<a<1$ gilt,="" wird="" der="" graph="" an="" y-achse="" gespiegelt.="" beachte,="" dass="" die="" grenzwerte="" sich="" ändern="" *="" $\lim\limits_{x\to="" \infty}="" a^x="0$" -\infty}="" ##="" beispiel="" für="" exponentialfunktionen="" und="" deren="" ableitung="" ###="" 1=""

$f(x)=e^{4x}$

Zur Ableitung dieser Funktion wird die Kettenregel verwendet. Die äußere Funktion ist $e^y$ und die innere Funktion $y=4x$ mit der Ableitung $y'=4$. Damit ist die Ableitung gegeben durch

$f'(x)=e^{4x}\cdot 4=4e^{4x}$

Dies kann verallgemeinert werden zu

$(e^{kx})'=ke^{kx}$

.

Beispiel 2

$f(x)=e^{0,5x-4}$

Auch hier wird die Kettenregel verwendet. Die äußere Funktion ist wiederum $e^y$. Die innere Funktion ist die lineare Funktion $y=0,5x-4$ mit der Ableitung $y'=0,5$. Nun kannst du die Funktion ableiten.

$f'(x)=e^{0,5x-4}\cdot 0,5=0,5e^{0,5x-4}$

Dies kann ebenfalls verallgemeinert werden zu

$(e^{kx+l})'=ke^{kx+l}$.

Beispiel 3

$f(x)=x\cdot e^x$

Diese Funktion wird mit der Produktregel abgeleitet. Diese lautet in der Kurzschreibweise $(u\cdot v)'=u'\cdot v+u\cdot v'$. Damit ist die Ableitung dieser Funktion gegeben durch:

$\begin{array}{rclll} f'(x)&=&1\cdot e^x+x\cdot e^x&|&(e^x)'=e^x\\ &=&(1+x)e^x&|&\text{ Ausklammern}\\ &=&(x+1)e^x \end{array}$

Beispiel 4

$f(x)=e^{0,5x}(x^2+1)$

Auch diese Funktion wird mit der Produktregel abgeleitet sowie mit der Kettenregel:

$\begin{array}{rclll} f'(x)&=&0,5e^{0,5x}(x^2+1)+e^{0,5x}\cdot 2x\\ &=&e^{0,5x}(0,5x^2+2x+0,5)&|&\text{ Ausklammern} \end{array}$

</a<1$>