Räumliches Koordinatensystem

Inhaltsverzeichnis zum Thema

• Das zweidimensionale Koordinatensystem
• Das dreidimensionale Koordinatensystem
• Aufbau eines dreidimensionalen Koordinatensystems
• Einzeichnen von Punkten im dreidimensionalen Koordinatensystem
• Objekte im dreidimensionalen Koordinatensystem

Das zweidimensionale Koordinatensystem

Wenn du zum Beispiel Funktionsgraphen darstellen möchtest, verwendest du ein zweidimensionales (ebenes) Koordinatensystem. Dieses besteht aus zwei Achsen, der $x$- und der $y$-Achse, welche sich in einem rechten Winkel schneiden. Die $x$-Achse wird auch Abzisse und die $y$-Achse Ordinate genannt.

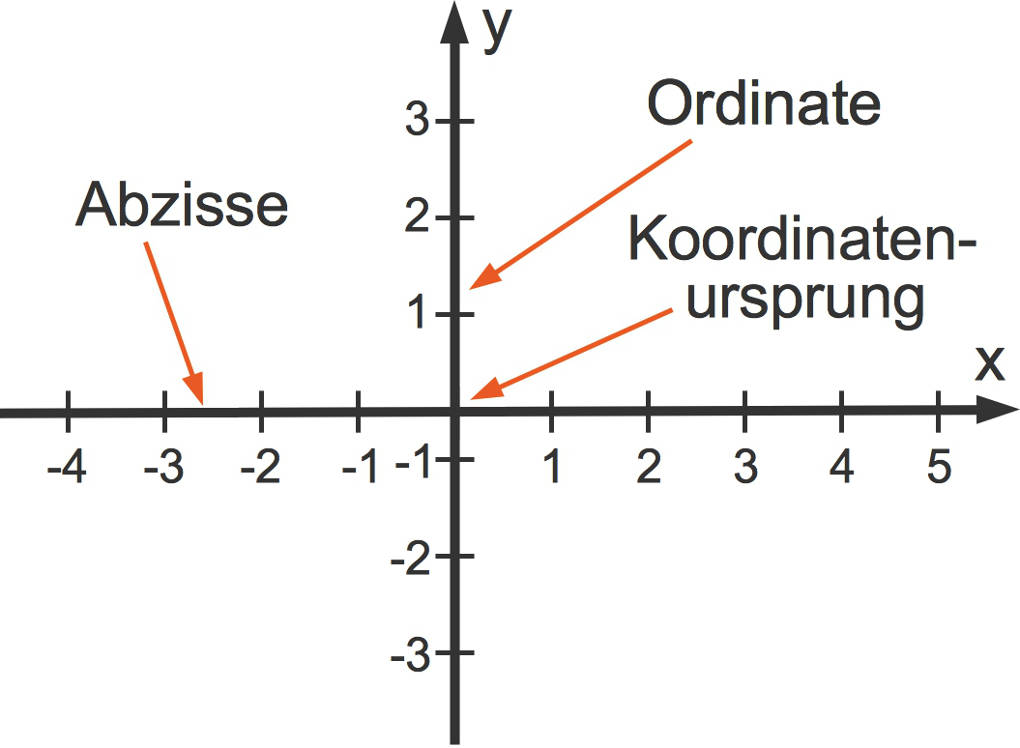
In ein solches Koordinatensystem kannst du Punkte oder, wie bereits erwähnt, Funktionsgraphen eintragen.

Das dreidimensionale Koordinatensystem

Wenn zu der $x$- und $y$-Koordinate noch eine weitere Koordinate hinzukommt, erhältst du ein dreidimensionales Koordinatensystem. Statt dreidimensional kannst du auch räumlich sagen. Die hinzukommende Koordinate ist die $z$-Koordinate.

Aufbau eines dreidimensionalen Koordinatensystems

Ausgehend von dem zweidimensionalen Koordinatensystem kannst du ein dreidimensionales zeichnen. Die $x$-Achse wird im dreidimensionalen Koordinatensystem zur $y$-Achse und die $y$-Achse zur $z$-Achse. Die $x$-Achse im dreidimensionalen Koordinatensystem ragt in den Raum hinein, zeigt sozusagen auf dich. Wie kannst du einen solchen 3-D-Effekt erreichen?

• Du zeichnest die $x$-Achse in einem Winkel von $135^\circ$ zur positiven $y$-Achse.
• Bei der Skalierung der Achsen verwendest du bei der $y$- sowie $z$-Achse die gleichen Abstände. Bei der in den Raum ragenden $x$-Achse werden die Abstände kürzer gewählt.

Hier siehst du ein räumliches Koordinatensystem.

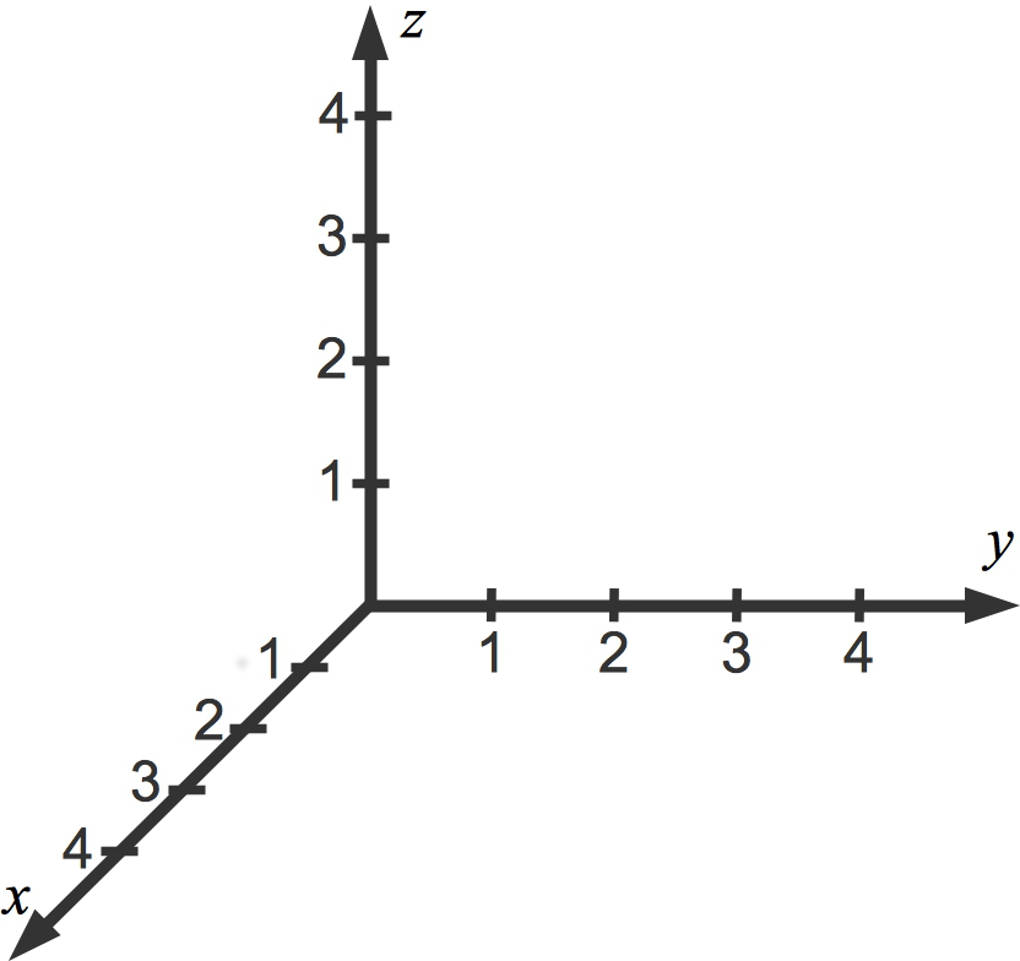
Du kannst auch die jeweiligen negativen Achsen einzeichnen. Mit Blick auf die Übersichtlichkeit wurde in dem obigen Bild darauf verzichtet.

Einzeichnen von Punkten im dreidimensionalen Koordinatensystem

Nun siehst du, wie du in das obige dreidimensionale Koordinatensystem Punkte einzeichnen kannst. Dies schauen wir uns an dem Beispiel des Punktes $G(3|4|2)$ an.

• Gehe zunächst $3$ Einheiten entlang der $x$-Achse.
• Von dort gehst du parallel zur $y$-Achse $4$ Einheiten.
• Schließlich gehst du weitere $2$ Einheiten parallel zur $z$-Achse.

Jede der hier angegebenen Bewegungen ist in dem folgenden Bild in Form eines Pfeiles dargestellt. Achte dabei auf die Perspektive: Wenn du $4$ Einheiten parallel zur $y$-Achse gehst, landest du nicht senkrecht unter $4$ auf der $y$-Achse:

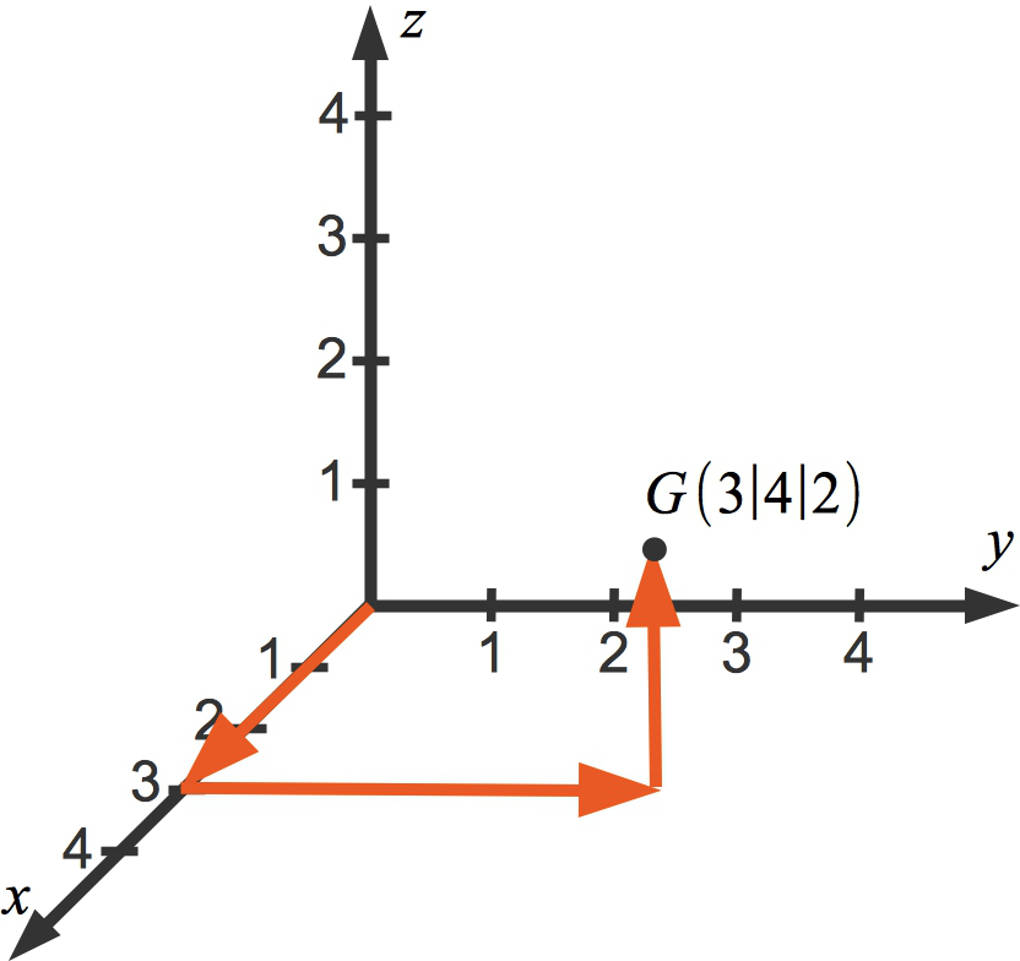
Wenn du den Abstand von Punkten im dreidimensionalen Koordinatensystem berechnen möchtest, verwendest du die folgende Formel. Gegeben seien die beiden Punkte $P\left(p_{x}|p_{y}|p_{z}\right)$ sowie $Q\left(q_{x}|q_{y}|q_{z}\right)$. Dann ist der Abstand dieser beiden Punkte wie folgt gegeben:

$d(P;Q)=\sqrt{\left(p_{x}-q_{x}\right)^2+\left(p_{y}-q_{y}\right)^2+\left(p_{z}-q_{z}\right)^2}$.

Das schauen wir uns nun an einem Beispiel an: $P(3|1|1)$ sowie $Q(-1|2|1)$.

$d(P;Q)=\sqrt{\left(3-(-1)\right)^2+\left(1-2\right)^2+\left(1-1\right)^2}=\sqrt{4^2+(-1)^2+0^2}=\sqrt{17}$

Objekte im dreidimensionalen Koordinatensystem

Nun weißt du, wie du Punkte in ein dreidimensionales Koordinatensystem eintragen kannst. So kannst du auch mit mehreren Punkten ein Schrägbild zum Beispiel eines Quaders erstellen.

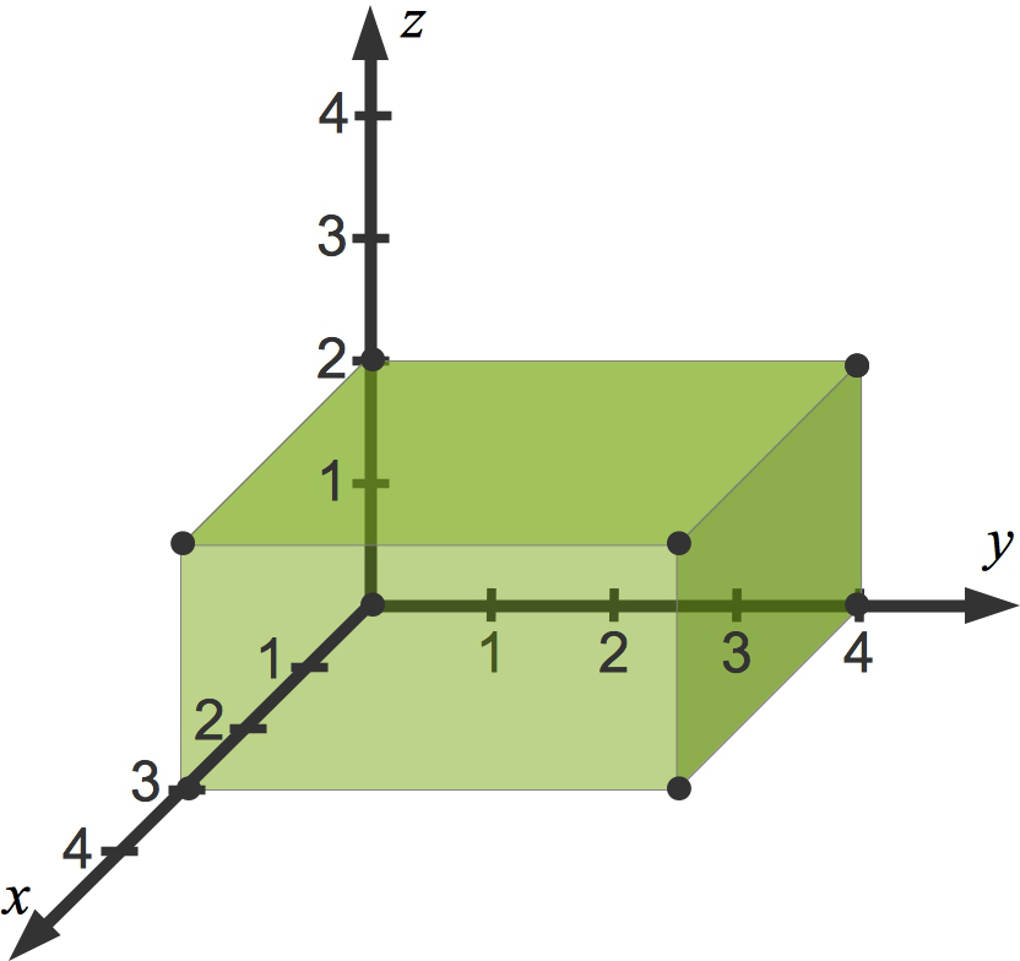
Nun kannst du zum Beispiel die Länge der Diagonale der rechten Seitenfläche dieses Quaders berechnen. Diese verbindet die Punkte $(0|4|0)$ sowie $(3|4|2)$:

$d(P;Q)=\sqrt{\left(0-3\right)^2+\left(4-4\right)^2+\left(0-2\right)^2}=\sqrt{(-3)^2+0^2+(-2)^2}=\sqrt{13}$.