Grundlagen zu Vektoren
Ein Vektor beschreibt eine Bewegung oder eine Verschiebung im Raum. Du kannst zum Beispiel einen Punkt A zu einem Punkt B verschieben.
Beliebteste Videos
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist ein Vektor?
- Vektoren als Bewegung von einem Punkt zu einem anderen
- Der Gegenvektor
- Der Nullvektor
- Der Verbindungsvektor
- Der Ortsvektor
Was ist ein Vektor?
Ein Vektor beschreibt eine Bewegung oder eine Verschiebung im Raum. Du kannst zum Beispiel einen Punkt $A$ zu einem Punkt $B$ verschieben. Du kannst auch einen Körper verschieben. Alle diese Verschiebungen können mit Hilfe von Vektoren dargestellt werden.
Hier siehst du ein Flugzeug, welches waagerecht von links nach rechts mit einer Geschwindigkeit von $\mathbf{300~km/h}$ fliegt. Darunter ist ein Flugzeug zu sehen, welches ebenfalls waagerecht, allerdings in die andere Richtung und mit doppelter Geschwindigkeit fliegt.
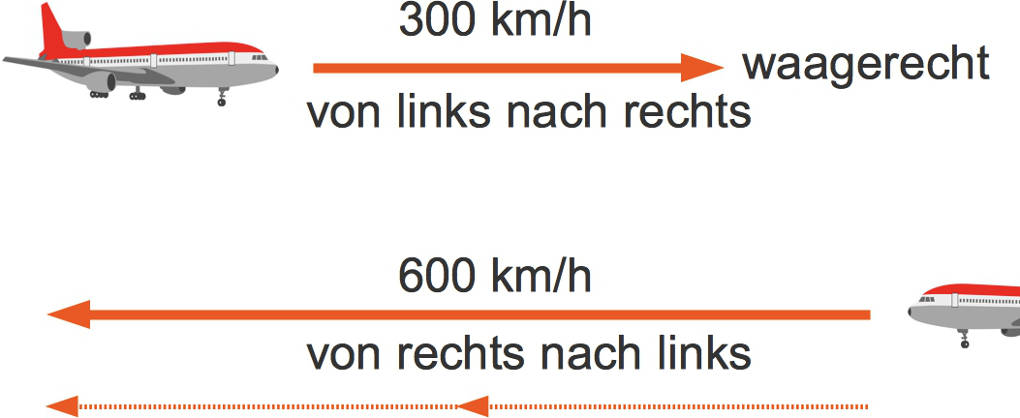
Diese Bewegungen werden durch Vektoren beschrieben: Vektoren werden als Pfeile dargestellt.
Vektoren haben
- eine Länge: Diese ist in diesem Beispiel die Geschwindigkeit. Das untere Flugzeug fliegt doppelt so schnell. Deshalb ist der Vektor doppelt so lang.
- eine Richtung: Diese stimmt bei beiden Flugzeugen überein. Beide Flugzeuge fliegen waagerecht. Allerdings fliegt das eine Flugzeug von links nach rechts und das andere von rechts nach links.
- eine Orientierung: Das obere Flugzeug fliegt von links nach rechts, während das untere von rechts nach links fliegt, also entgegengesetzt.
Vektoren als Bewegung von einem Punkt zu einem anderen
Stelle dir einen Vektor als die Bewegung von einem Punkt zu einem anderen vor.
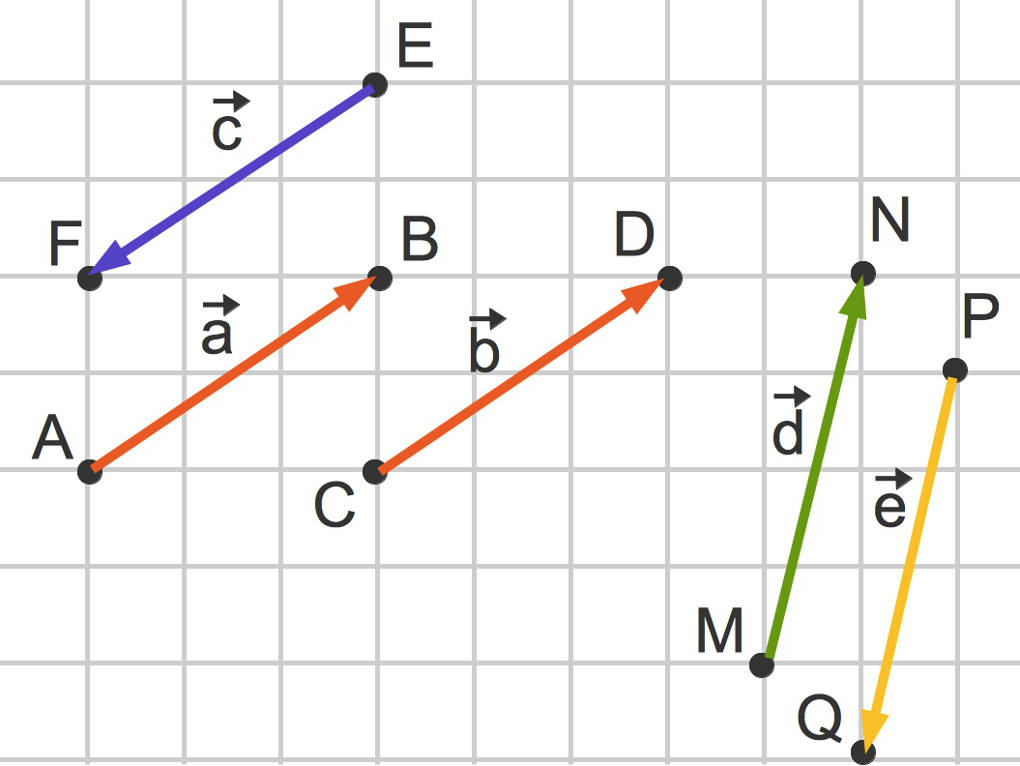
Zum Beispiel verläuft einer der beiden roten Vektoren von $A$ nach $B$: Ein Vektor wird mit einem Kleinbuchstaben und einem Pfeil darüber bezeichnet. Da der Vektor von $A$ nach $B$ verläuft, kann man den Vektor so schreiben: $\vec a=\vec{AB}$. Die übrigen Vektoren sind dann:
- $\vec b=\vec{CD}$
- $\vec c=\vec{EF}$
- $\vec d=\vec{MN}$
- $\vec e=\vec{PQ}$
Du siehst: Es wird immer zuerst der Punkt, von welchem der Vektor ausgeht, dies ist der Anfangspunkt, geschrieben und dann der Endpunkt.
Was fällt dir auf? Die Vektoren $\vec a$ und $\vec b$ haben die gleiche Länge, die gleiche Richtung und die gleiche Orientierung. Das bedeutet, dass diese beiden Vektoren gleich sind. Du kannst dies so schreiben
$\vec a=\vec b~\text{ oder }~\vec{AB}=\vec{CD}$
Der Gegenvektor
Der Vektor $\vec c$ hat die gleiche Richtung und Länge wie $\vec a$ und $\vec b$, jedoch eine andere Orientierung. Es gilt
$\vec c = -\vec a~\text{ oder }~\vec{EF}=-\vec{AB}$.
Der Vektor $\vec c$ wird als der Gegenvektor des Vektors $\vec a$ bezeichnet. Ebenso ist der Vektor $\vec a$ der Gegenvektor des Vektors $\vec c$. Die Vektoren $\vec d$ und $\vec e$ sind auch Gegenvektoren.
Der Nullvektor
Wenn der Anfangspunkt und der Endpunkt eines Vektors übereinstimmen, kannst du den Vektor $\vec{AA}$ verstehen als Bleibe bei $A$. Es findet also keine Bewegung statt. Dieser Vektor wird als Nullvektor bezeichnet: $\vec{AA}=\vec 0$, die Zahl $0$ mit einem Pfeil darüber.
Der Verbindungsvektor
Da der Vektor $\vec a=\vec{AB}$ von $A$ nach $B$ verläuft, also diese beiden Punkte miteinander verbindet, wird dieser Vektor auch als Verbindungsvektor der beiden Punkte $A$ und $B$ bezeichnet.
Der Ortsvektor
Wenn du in einem dreidimensionalen Koordinatensystem, dem $\mathbb{R}^3$, einen Vektor von dem Koordinatenursprung $O(0|0|0)$ zu einem Punkt $P(p_x|p_y|p_y)$ zeichnest, erhältst du den Ortsvektor des Punktes $P$. Dieser wird mit dem entsprechenden Kleinbuchstaben und einem Pfeil darüber geschrieben:
$\vec p=\vec{OP}$.
Vektoren in der Koordinatenschreibweise
Ein Vektor, zum Beispiel $\vec a$, hat im $\mathbb{R}^2$ zwei und im $\mathbb{R}^3$ drei Koordinaten. Diese Koordinaten werden entweder mit den Indizes $1$, $2$ (, $3$) oder auch mit $x$, $y$ (, $z$) bezeichnet und spaltenweise aufgeschrieben.
Der Vektor $\vec a$ sieht im $\mathbb{R}^2$ so:
$\vec a=\begin{pmatrix} a_1 \\ a_2 \end{pmatrix}=\begin{pmatrix} a_x \\ a_y \end{pmatrix}$
und im $\mathbb{R}^3$ so:
$\vec a=\begin{pmatrix} a_1 \\ a_2\\ a_3 \end{pmatrix}=\begin{pmatrix} a_x \\ a_y\\ a_z \end{pmatrix}$
aus.
- Damit ist der Ortsvektor eines Punktes der Vektor, welcher die gleichen Koordinaten wie der Punkt hat. Sei zum Beispiel der Punkt $P(1|3|-1)$, dann ist der zugehörige Ortsvektor gegeben durch
$\quad~~~\vec p=\vec{OP}=\begin{pmatrix} 1 \\ 3\\ -1 \end{pmatrix}$
- Den Verbindungsvektor $\vec e=\vec{PQ}$ zweier Vektoren erhältst du, indem du die Differenz der Koordinaten des Ortsvektors des Endpunktes und denen des Anfangspunktes bestimmst:
$\quad~~~\vec e=\begin{pmatrix} q_x -p_x\\ q_y-p_y\\ q_z-p_z \end{pmatrix}$
Verschieben eines Punktes um einen Vektor
Schaue dir noch einmal das Beispiel mit dem Flugzeug an. Der Einfachheit halber sei die aktuelle Position des Flugzeuges ein Punkt $F(-3|12|11)$, alle Angaben in Kilometer. Das bedeutet, das Flugzeug fliegt in $11~km$ Höhe. Der Vektor, welcher die Bewegung des Flugzeugs angibt, ist
$\vec v=\begin{pmatrix} 0\\ 300\\ 0 \end{pmatrix}$,
da das Flugzeug $300~km$ in einer Stunde von links nach rechts fliegt. Wo befindet sich das Flugzeug nach einer Stunde? Hierfür verschiebst du den Punkt $F$ einmal um den Vektor $\vec v$:
$\begin{pmatrix} -3\\ 12\\ 11 \end{pmatrix}+\begin{pmatrix} 0\\ 300\\ 0 \end{pmatrix}=\begin{pmatrix} -3\\ 312\\ 11 \end{pmatrix}$.
Das Flugzeug befindet sich also nach einer Stunde an der Position $F'(-3|312|11)$.
Der Betrag oder die Länge eines Vektors
Der Betrag oder auch die Länge eines Vektors kannst du wie folgt berechnen: du
- quadrierst jede Koordinate des Vektors,
- addierst die Quadrate und
- ziehst zuletzt die Wurzel aus der Summe.
$|\vec a|=\sqrt{a_x^2+a_y^2}$; im $\mathbb{R}^2$
und
$|\vec a|=\sqrt{a_x^2+a_y^2+a_z^2}$; im $\mathbb{R}^3$.
Begründung für diese Formel im $\mathbb{R}^2$
Wenn du den Vektor $\vec a$ so legst, dass er im Koordinatenursprung beginnt, erhältst du die folgende Situation:
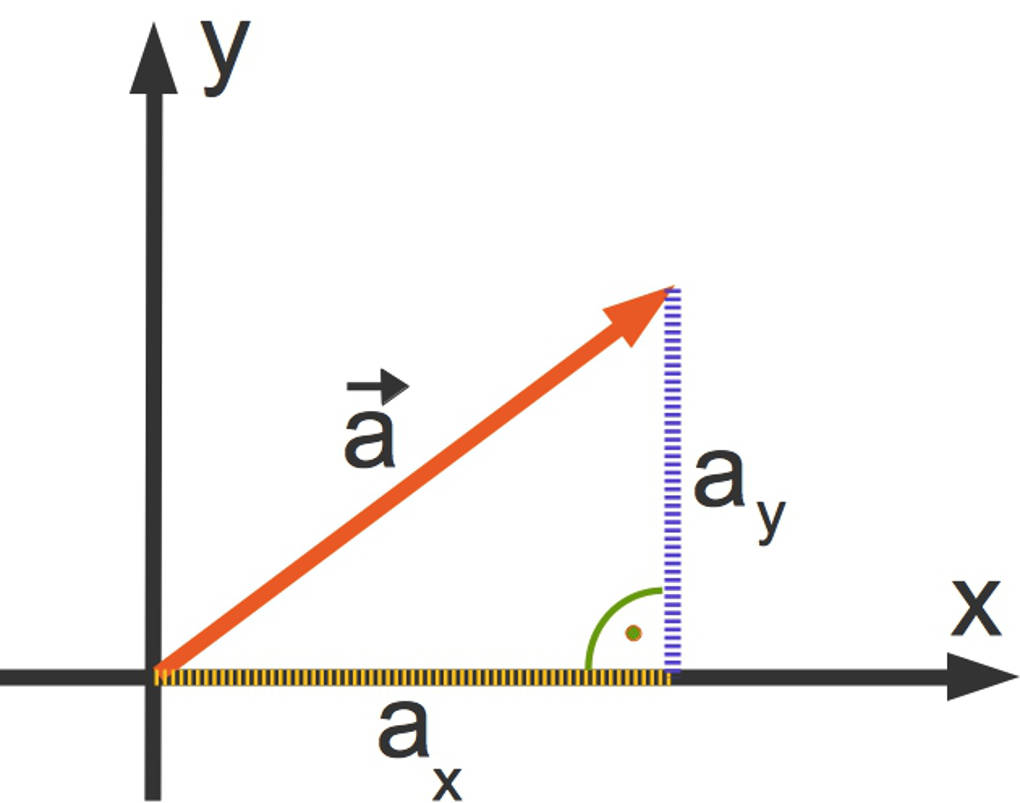
Die beiden Koordinaten $a_x$ sowie $a_y$ des Vektors sind die Katheten eines rechtwinkligen Dreiecks. Die Hypotenuse stellt den Vektor $\vec a$ dar. Nach dem Satz des Pythagoras gilt dann für die das Quadrat der Länge dieses Vektors:
$|\vec a|^2=a_x^2+a_y^2$.
Wenn du auf beiden Seiten die Quadratwurzel ziehst, erhältst du die Formel für die Länge eines Vektors im $\mathbb{R}^2$. Ebenso kannst du diese Formel für Vektoren im $\mathbb{R}^3$ nachweisen. Der Satz des Pythagoras wird dann zweimal angewendet.
Der Abstand zweier Punkte
Den Abstand zweier Punkte kannst du mit dieser Formel auch berechnen. Der Abstand zweier Punkte ist die Länge des Verbindungsvektors dieser beiden Punkte:
$d(P;Q)=|\vec{PQ}|=\sqrt{(q_x-p_x)^2+(q_y-p_y)^2+(q_z-p_z)^2}$.
- Du bildest also die Differenz der Koordinaten der beiden Punkte,
- quadrierst diese Differenzen,
- addierst die Quadrate und
- ziehst zuletzt die Wurzel aus der Summe.
Beispiel: Berechne den Abstand der beiden Punkte $P(8|-10|5)$ sowie $Q(12|-2|6)$.
$d(P;Q)=|\vec{PQ}|=\sqrt{(12-8)^2+(-2-(-10))^2+(6-5)^2}=\sqrt{81}$=9
Der Abstand der beiden Punkte beträgt somit 9 Längeneinheiten (kurz: LE).
Alle Videos zum Thema
Videos zum Thema
Grundlagen zu Vektoren (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Grundlagen zu Vektoren (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter





 Was ist ein Vektor?
Was ist ein Vektor?
 Betrag eines Vektors
Betrag eines Vektors









