Strahlensätze
Strahlensatzfigur, Strahlenabschnitt, Parallelenabschnitt, Strahlensätze an sich schneidenden Geraden
Beliebteste Videos und Lerntexte
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Einleitung Strahlensätze
- Erster Strahlensatz
- Zweiter Strahlensatz
- Gültigkeit der Strahlensätze beidseitig vom Scheitelpunkt
- Anwendungsbeispiel Turmhöhe
- Anwendungsbeispiel Drahtseil
Einleitung Strahlensätze
Die Strahlensätze gehören zu den wichtigsten Lehrsätzen der Geometrie. Sie bilden die Grundlage der zentrischen Streckung, einer der zentralen Ähnlichkeitsabbildungen.
Die Strahlensätze basieren auf der Grundkonstruktion, dass zwei von einem Punkt ausgehende Strahlen von zwei zueinander parallelen Geraden geschnitten werden. Dadurch werden die Strahlen in verschiedene Abschnitte unterteilt, über deren Verhältnisse die Strahlensätze verschiedene Aussagen formulieren.
Erster Strahlensatz
Werden zwei Strahlen mit einem gemeinsamen Scheitelpunkt von zwei zueinander parallelen Geraden geschnitten, so verhalten sich die Längen der Abschnitte auf dem einen Strahl wie die entsprechenden Abschnitte auf dem anderen Strahl.

Du kannst auf jedem Strahl zwei Abschnitte ablesen: zwischen $S$ und $A$ sowie $S$ und $A'$ bzw. zwischen $S$ und $B$ sowie $S$ und $B'$. In Formeln lässt sich also die Aussage formulieren:
$\frac{\overline{SA}}{\overline{SA'}}=\frac{\overline{SB}}{\overline{SB'}}$
Beispiel zum ersten Strahlensatz
Gilt für die Strecken einer Strahlensatzfigur beispielsweise
$\overline{SA}=2~\text{cm},~\overline{SB}=4~\text{cm},~\overline{SA'}=6~\text{cm}$
dann berechnet sich der fehlende Abschnitt zu
$\overline{SB'}=\overline{SB}\cdot\frac{\overline{SA'}}{\overline{SA}}= 4~\text{cm}\cdot\frac{6~\text{cm}}{2~\text{cm}}=12~\text{cm}$
Den ersten Strahlensatz kannst du auch auf die anderen Abschnitte der Strahlen erweitern, also diejenigen, die nicht in S beginnen. Demnach gilt zusätzlich:
$\frac{\overline{SA}}{\overline{AA'}}=\frac{\overline{SB}}{\overline{BB'}} \text{ und } \frac{\overline{SA'}}{\overline{AA'}}=\frac{\overline{SB'}}{\overline{BB'}}$
Sind z.B.
$\overline{SA}=2,4~\text{cm},~\overline{AA'}=3,2~\text{cm},~\overline{BB''}=3~\text{cm}$
gegeben, dann berechnet sich die fehlende Streckenlänge zu
$\overline{SB}=\overline{BB'}\cdot\frac{\overline{SA}}{\overline{AA'}}= 3~\text{cm}\cdot\frac{2,4~\text{cm}}{3,2~\text{cm}}=2,25~\text{cm}$
Zweiter Strahlensatz
Auch die Abschnitte auf den Parallelen, die das Strahlenpaar schneiden, stehen in bestimmten Verhältnissen zueinander. Diese werden im zweiten Strahlensatz formuliert:
Werden zwei Strahlen mit einem gemeinsamen Scheitelpunkt S von zwei zueinander parallelen Geraden geschnitten, so verhalten sich die Längen der von S ausgehenden Abschnitte auf den Strahlen wie die Längen der zugehörigen Abschnitte auf den Parallelen (siehe Abbildung oben).
In Formeln:
$\frac{\overline{AB}}{\overline{A'B'}}=\frac{\overline{SA}}{\overline{SA'}} \text{ und } \frac{\overline{AB}}{\overline{A'B'}}=\frac{\overline{SB}}{\overline{SB'}}$
Beispiel zum zweiten Strahlensatz
Ein typisches Beispiel für die Anwendung des zweiten Strahlensatzes ist die Bestimmung der Höhe eines Objekts (z. B. eines Turms) durch den Vergleich mit einer bekannten Höhe.
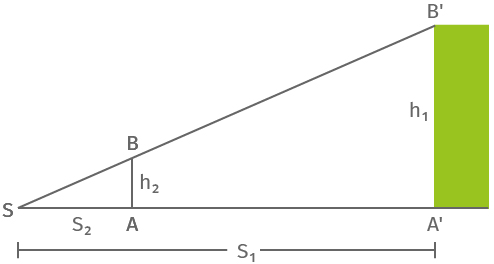
Die unbekannte Höhe des Turms kannst du mit Hilfe der Schattenlänge eines Stabes mit einer bekannten Länge (z.B. 1m) bestimmen. Hierzu wird der Stab senkrecht so aufgestellt, dass das Ende seines Schattens mit dem Schattenende des Turms in S zusammenfällt. Nach dem zweiten Strahlensatz verhält sich die unbekannte Höhe des Turms zur Höhe des Stabes wie die Länge des Turmschattens (z.B. 50 m) zur Länge des Stabschattens (z.B. 4 m):
$\frac{\text{Höhe des Turms}}{\text{Länge des Stabs}}= \frac{h_1}{1~ \text{m}}=\frac{50 \text{m}}{4~\text{m}}=12,5$
$\Rightarrow h_1=12,5~\text{m}$
Der Turm ist also 12,5 m hoch.
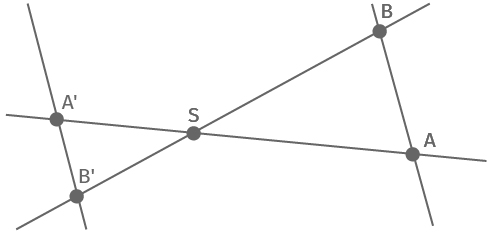
Gültigkeit der Strahlensätze beidseitig vom Scheitelpunkt
Da wir nur die Längen von Strecken, nicht jedoch ihre Ausrichtung betrachten, gelten beide Strahlensätze auch dann unverändert, wenn die Parallelen auf verschiedenen Seiten des Scheitelpunkts liegen.
Anwendungsbeispiel Turmhöhe
Paul möchte die Höhe $h$ eines Turms mit Hilfe eines Stabes bestimmen. Er steht in $52~\text{m}$ Entfernung von dem Turm. Nun stellt er einen $2,90~\text{m}$ langen Stab senkrecht so auf, dass er die Turmspitze genau auf der Höhe der Spitze des Stabes sehen kann. Dafür muss er den Stab in $2~\text{m}$ Entfernung aufstellen. Paul ist $1,60~\text{m}$ groß.
Fertige zunächst eine Skizze an, welche dem beschriebenen Zusammenhang entspricht. Diese muss nicht maßstabgetreu sein.
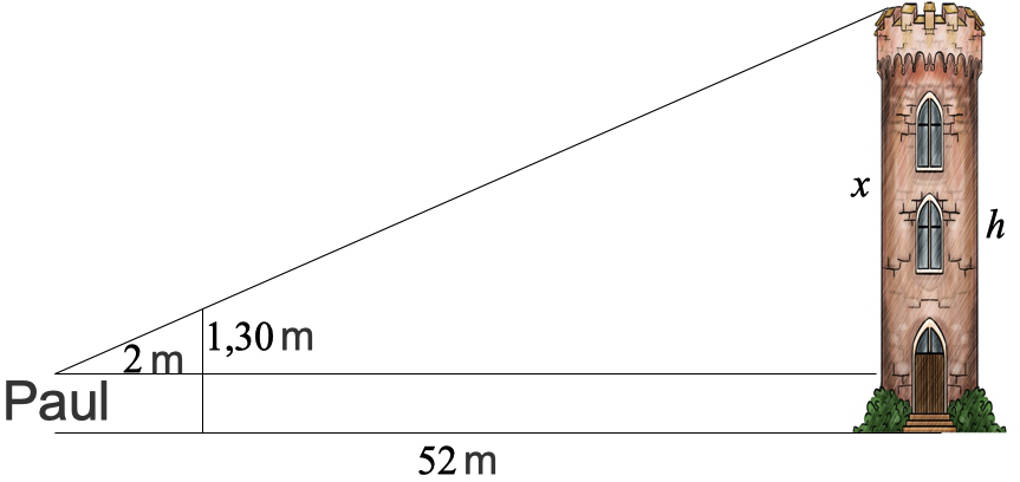
Du kannst den zweiten Strahlensatz verwenden: Die Größe $x$ verhält sich zu $1,30=2,90-1,60$ wie die Entfernung von Paul zu dem Turm zu der zu dem Stab. Beachte, dass du von der Höhe des Stabes die Körpergröße von Paul subtrahieren musst.
$\frac{x}{1,30}=\frac{52}{2}$
Multipliziere nun mit $1,30$, so erhältst du $x=33,80$. Dies ist noch nicht die gesuchte Höhe des Turms. Du musst noch Pauls Körpergröße hinzuaddieren und erhältst dann $h=33,80+1,60=35,40$. Der Turm ist also $35,40~\text{m}$ hoch.
Anwendungsbeispiel Drahtseil
Ein Drahtseilartist möchte auf einem Drahtseil auf einen Turm klettern. Er kennt die folgenden Größen:
- Sein horizontaler Abstand zu dem Fuß des Turm beträgt $120~\text{m}$.
- In $80~\text{m}$ Entfernung zu dem Drahtseilkünstler steht eine Hilfskonstruktion zur Befestigung des Seils.
- Das Seil ist bis zu dieser Konstruktion bereits $95~\text{m}$ lang.
Der Drahtseilartist überlegt, ob ein $150~\text{m}$ langes Seil ausreicht.
Was musst du berechnen? Richtig: Gesucht ist die Gesamtlänge des Seils.
Tipp: Fertige dir eine Skizze an. Der Drahtseilkünstler $D$ steht an der Stelle von $S$ aus der obigen Strahlensatzfigur. Nun kannst du die einzelnen Strecken einzeichnen:
- $\overline{DA}=80~\text{m}$
- $\overline{DA'}=120~\text{m}$
- $\overline{DB}=95~\text{m}$
Los geht's: Setze die bekannten Größen in die Formel ein. Gesucht ist $\overline{DB'}$.
$\frac{80~\text{m}}{120~\text{m}}=\frac{95~\text{m}}{\overline{DB'}}$
Du siehst, dass die gesuchte Größe im Nenner steht. Bilde auf beiden Seiten des Gleichheitszeichens den Kehrwert und forme die Gleichung um:
$\begin{array}{rclll} \frac{120~\text{m}}{80~\text{m}}&=&\frac{\overline{DB'}}{95~\text{m}}&|&\cdot 95~\text{m}\\\\ \frac{120~\text{m}}{80~\text{m}}\cdot 95~\text{m}&=&\overline{DB'}\\\\ 142,5~\text{m}&=&\overline{DB'} \end{array}$
Das Seil ist also insgesamt $142,5~\text{m}$ lang. Das bedeutet, dass das Seil, welches der Artist zur Verfügung hat, sicher ausreichend ist.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Strahlensätze (4 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Strahlensätze (5 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter










 Strahlensätze
Strahlensätze
 Erster Strahlensatz – Einführung
Erster Strahlensatz – Einführung
 Zweiter Strahlensatz – Einführung
Zweiter Strahlensatz – Einführung
 Erweiterung der Strahlensätze
Erweiterung der Strahlensätze
 Strahlensätze – Entfernungen im Gelände
Strahlensätze – Entfernungen im Gelände









