Kreisausschnitt, Kreisbogen und Kreisabschnitt

Inhaltsverzeichnis zum Thema

• Der Kreisbogen
• Der Kreisausschnitt
• Die Pizza
• Der Kreisabschnitt

Der Kreisbogen

In einem Kreis können wir zwei besondere Flächen betrachten: den Kreisausschnitt und den Kreisabschnitt. Beginnen wir aber zunächst mit dem Kreisbogen, den wir sowohl für Kreisausschnitte als auch für Kreisabschnitte benötigen.

Unter einem Kreisbogen verstehen wir einen Teil des Kreises. Dieser wird - wie du in der Abbildung erkennen kannst - mit dem Buchstaben $b$ bezeichnet.

Die Länge des Kreisbogens $b$ hängt vom Winkel $\alpha$ im Kreismittelpunkt ab. Dieser Winkel heißt Mittelpunktswinkel, weil dessen Scheitelpunkt der Kreismittelpunkt $M$ ist. Ist $\alpha = 360^\circ$, haben wir einen vollständigen Kreis. Ein halber Kreis hat den Mittelpunktswinkel $\alpha = 180^\circ$.

Die Länge des Kreisbogens $b$ berechnet sich mithilfe der folgenden Formel:

$b = \frac{\alpha}{180^\circ} \cdot \pi \cdot r$

Wir setzen nun einmal $\alpha = 360^\circ$ in diese Formel ein. Wenn du die Formel für den Umfang bereits kennst, siehst du, dass die Länge des Kreisbogens $b$ dem Umfang $U$ des gesamten Kreises entspricht:

$b = \frac{360^\circ}{180^\circ} \cdot \pi \cdot r = 2 \cdot \pi \cdot r = U$

Der Kreisausschnitt

So, wie der Kreisbogen ein Teil des Kreises ist, ist der Kreisausschnitt ein Teil der Kreisfläche.

Die Fläche eines Kreisausschnittes wird auch Kreissektor genannt. Das kannst du dir wie die Stücke eines Kuchens vorstellen. Ein solcher Kreisausschnitt ist durch den Mittelpunktswinkel $\alpha$ definiert, der auch Zentriwinkel genannt wird.

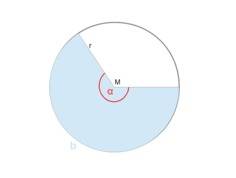
Ein Kreisausschnitt ist nun der Teil der Kreisfläche, der von den Schenkeln des Mittelpunktswinkels $\alpha$ und dem zugehörigen Kreisbogen $b$ begrenzt wird. Bekanntlich lässt sich die Fläche eines Kreises mit dieser Formel berechnen:

$A = \pi \cdot r^2$

Die anteilige Fläche $A$ eines Kreisausschnitts berechnest du dann nach der folgenden Formel:

$b = \frac{\alpha}{360^\circ} \cdot \pi \cdot r^2$

Wenn du $\alpha = 360^\circ$ einsetzt, erhältst du wieder den Flächeninhalt des gesamten Kreises:

$A = \frac{360^\circ}{360^\circ} \cdot \pi \cdot r^2 = \pi \cdot r^2$

Die Pizza

Du möchtest mit deiner Freundin eine Pizza backen. Die Pizza hat einen Radius von $r = 15~cm$ und wird in vier gleich große Stücke aufgeteilt. Jedes Stück hat also den Mittelpunktswinkel $\alpha = \frac{360^\circ}4 = 90 ^\circ$.

Da du den Radius der Pizza kennst, kannst du auch die Fläche eines Viertels berechnen. Der entsprechende Winkel beträgt $90^\circ$:

$ A = \frac{90^\circ}{360^\circ} \cdot \pi \cdot (15 ~cm)^2= \frac14 \cdot \pi \cdot 225~cm^2 \approx 176,7 ~cm^2$

Der Kreisabschnitt

Bei dem Kreisabschnitt handelt es sich ebenso um eine Teilfläche der Kreisfläche.

Der Kreisabschnitt wird auch Kreissegment genannt und ist durch den Kreisbogen $b$ und eine Kreissehne begrenzt. Unter einer Kreissehne versteht man die Strecke zwischen zwei Punkten des Kreises.