Winkelmaß und Bogenmaß
Einfach lernen mit Videos, Übungen, Aufgaben & Arbeitsblättern
Beliebteste Videos
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Winkel im Winkelmaß
- Winkel im Bogenmaß
- Umrechnungen
- Vom Bogenmaß in das Winkelmaß
- Vom Winkelmaß in das Bogenmaß
Winkel im Winkelmaß
Als du Winkel kennengelernt hast, wurden sie immer im Winkelmaß, auch als Gradmaß bezeichnet, angegeben. Dieses Maß erkennst du an dem Grad-Zeichen, einem kleinen hochgestellten Kreis, zum Beispiel $\alpha=80^°$, also $80$ Grad. Erinnere dich: Ein Vollwinkel, also eine gesamte Umdrehung (wie ein Kreis), hat eine Größe von $360^°$.
Wenn du mit trigonometrischen Funktionen $\sin$, $\cos$ oder $\tan$ und Angaben im Gradmaß rechnest, muss der Taschenrechner auf Degree, also Gradmaß, eingestellt sein. Dies erkennst du häufig an dem kleinen D oder DEG auf dem Display deines Taschenrechners.
Winkel im Bogenmaß
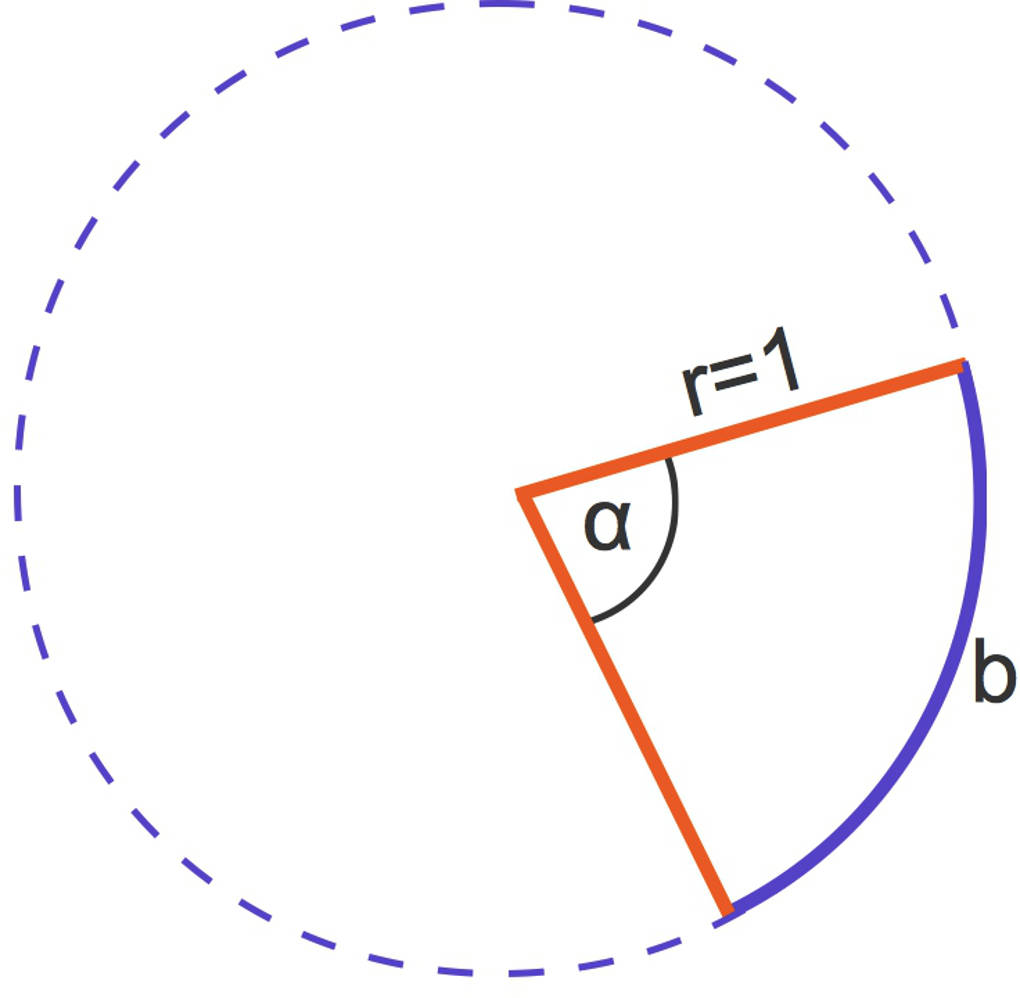
Dieser Kreis, ein Einheitskreis, hat den Radius $r=1$ und somit den Umfang $U=2\pi$. Zu dem eingezeichneten Winkel $\alpha$ gehört der blau gezeichnete Abschnitt des Umfangs des Kreises. Dieser wird als Kreisbogen oder kurz als Bogen bezeichnet. Die Maßeinheit eines Kreisbogens ist Unterschied zum Gradmaß eine Längeneinheit. Im Bezug auf den Winkel $\alpha$ wird diese Maßeinheit als Bogenmaß bezeichnet.
Wenn du mit trigonometrischen Funktionen Kurvendiskussionen durchführst, wird das Bogenmaß verwendet. Dafür muss der Taschenrechner auf Radiant, also Bogenmaß, eingestellt sein. Dies erkennst du an dem kleinen R oder RAD auf dem Display deines Taschenrechners.
Umrechnungen
Am Einheitskreis oben kannst du erkennen: Der Vollwinkel $360^°$ entspricht genau dem Kreisumfang $2\pi$. Und der Winkel $\alpha$ entspricht genau dem Bogen $b$.
Dies kannst du als Gleichung aufschreiben:
$\quad~~~\frac{2\pi}{360^°}=\frac{b}{\alpha}$.
Mit Hilfe dieser Gleichung kannst du nun von Grad- in Bogenmaß und anders herum umrechnen.
Vom Bogenmaß in das Winkelmaß
Wie kannst du die Länge des Kreisbogens $b$ in den zugehörigen Winkel $\alpha$ umrechnen?
- Nimm die Gleichung von eben als Grundlage:
$\quad~~~\frac{2\pi}{360^°}=\frac{b}{\alpha}$
- Bilde auf beiden Seiten der obigen Gleichung den Kehrwert:
$\quad~~~\frac{360^°}{2\pi}=\frac{\alpha}{b}$
- Multipliziere dann mit $b$:
$\quad~~~\alpha=\frac{360^°\cdot b}{2\pi}$
Üblicherweise ist das Bogenmaß als Vielfaches von $\pi$ gegeben.
- Wenn $b=\pi$, dann ist
$\quad~~~\alpha=\frac{360^°\cdot \pi}{2\pi}=\frac{360^°}{2}=180^°$
- Wenn $b=0,5\pi$, dann ist
$\quad~~~\alpha=\frac{360^°\cdot 0,5\pi}{2\pi}=\frac{360^°}{4}=90^°$
Vom Winkelmaß in das Bogenmaß
Wie kannst du den Winkel $\alpha$ in die zugehörige Länge des Kreisbogens $b$ umrechnen?
- Auch hier verwende die Gleichung:
$\quad~~~\frac{2\pi}{360^°}=\frac{b}{\alpha}$
- Multipliziere beide Seiten mit $\alpha$:
$\quad~~~b=\frac{2\pi\cdot \alpha}{360^°}$
Erinnere dich: $\alpha$ ist immer im Gradmaß angegeben.
- Wenn $\alpha=45^°$, dann ist
$\quad~~~b=\frac{2\pi\cdot 45^°}{360^°}=\frac14\pi$.
- Wenn $\alpha=180^°$, dann ist
$\quad~~~b=\frac{2\pi\cdot 180^°}{360^°}=\pi$.
Verwendung des Bogenmaßes
Das Bogenmaß verwendest du ausschließlich im Zusammenhang mit trigonometrischen Funktionen, zum Beispiel der Sinusfunktion $f(x)=\sin(x)$. Dabei ist die Variable $x$ im Bogenmaß gegeben. Die trigonometrischen Funktionen sind für alle reellen Zahlen definiert.
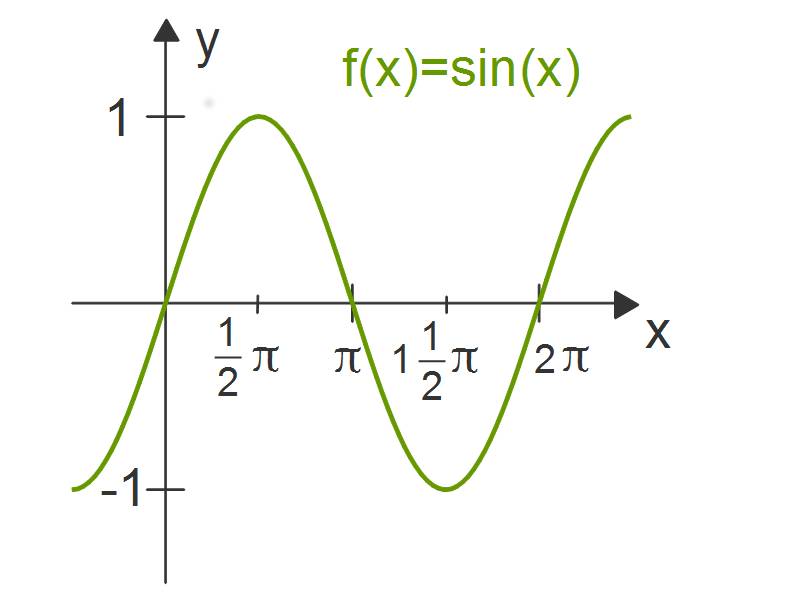
Die Sinusfunktion ist $2\pi$ periodisch. Das bedeutet, dass der Verlauf des Graphen sich jeweils nach einem Intervall der Länge $2\pi$ wiederholt.
- Ein Winkel kann auch größer als $2\pi$ sein: Da $2\pi$ dem Vollkreis $360^°$ entspricht, muss jedes Bogenmaß, welches größer ist als $2\pi$ einem Winkel größer als $360^°$ entsprechen. Dies entspricht dem mehrmaligen Durchlaufen des Kreises. Die Sinuswerte wiederholen sich: Zum Beispiel ist $\sin(0,5\pi)=\sin(2,5\pi)=1$.
- Ebenso kann ein Winkel negativ sein: Winkel werden üblicherweise entgegen dem Uhrzeigersinn gemessen. Wenn du die Richtung änderst erhältst du negative Winkel. Auch hier kannst du die $2\pi$-Periodizität verwenden: $\sin(0,5\pi)=\sin(-1,5\pi)=1$.
Mit Hilfe des Bogenmaßes kann die Periodizität der Sinusfunktion so dargestellt werden:
$\quad~~~\sin(x)=\sin(x+2k\pi)$, wobei $k\in \mathbb{Z}$.
Ebenso können die Nullstellen dargestellt werden:
$\quad~~~\sin(x)=0~\Leftrightarrow~x=2k\pi$, wobei $k\in \mathbb{Z}$.
Alle Videos zum Thema
Videos zum Thema
Winkelmaß und Bogenmaß (1 Video)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Winkelmaß und Bogenmaß (1 Arbeitsblatt)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter




 Gradmaß und Bogenmaß – Umrechnung
Gradmaß und Bogenmaß – Umrechnung












