Extremwertaufgaben mit quadratischen Funktionen
Scheitelpunkt bestimmen, quadratische Zielfunktion, Optimierungsaufgaben, Nebenbedingung
Beliebteste Videos und Lerntexte
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was sind Extremwertaufgaben?
- Was ist eine quadratische Funktion?
- Beispiel einer Extremwertaufgabe mit quadratischer Funktion
Was sind Extremwertaufgaben?
Wahrscheinlich hast du schon viele Extremwertaufgaben im Kopf gelöst, ohne viel darüber nachgedacht zu haben. Glaubst du nicht? Vielleicht hast du dir schon mal überlegt, welche und wie viele Dinge du für dein Taschengeld kaufen kannst. Tatsächlich ist das auch eine Art von Extremwertaufgabe. Denn vermutlich wolltest du möglichst viel für dein Geld haben. Und dein Restgeld minimieren, es sei denn, du gehörst zu der aussterbenden Rasse der Sparfüchse.
In der Mathematik sucht eine Extremwertaufgabe nach einem maximalen oder minimalen, also extremen Wert einer mathematischen Fragestellung. Die Fragestellung muss dafür erst einmal als mathematische Funktion formuliert werden. Diese kann dann von einer oder mehreren Variablen abhängen.
In der Schule begegnen dir normalerweise nur Funktionen, die von einer Variablen z.B. $x$ abhängen. Die Funktionsgleichung, in der $x$ vorkommt, bestimmt dann den zugehörigen Wert $y$. Dieser soll schließlich möglichst klein oder möglichst groß werden. Manchmal ist die Funktionsgleichung auch eine quadratische Funktion.
Was ist eine quadratische Funktion?
Quadratische Gleichungen kannst du sehr leicht erkennen. Sieh dir einfach den höchsten Exponenten, also die Hochzahl von $x$ an. Ist er genau $2$ und steht $x$ nirgendwo im Nenner? Du hast sie soeben entlarvt! Das Fahndungsbild der allgemeinen quadratischen Funktion sieht übrigens so aus:
$ f(x) = a\cdot x^{2} + b\cdot x + c $
Diese Darstellung wird Normalform genannt - mit $a,b,c \in \mathbb{R}$ und $a\neq 0$. Der Name der Funktion (hier $f$) ist dabei egal. Genauso, ob es den Anteil $b\cdot x$ oder $c$ gibt. Wichtig ist nur der Teil $x^{2}$.
Der Graph, also die Zeichnung einer solchen Funktion, wird Parabel genannt.
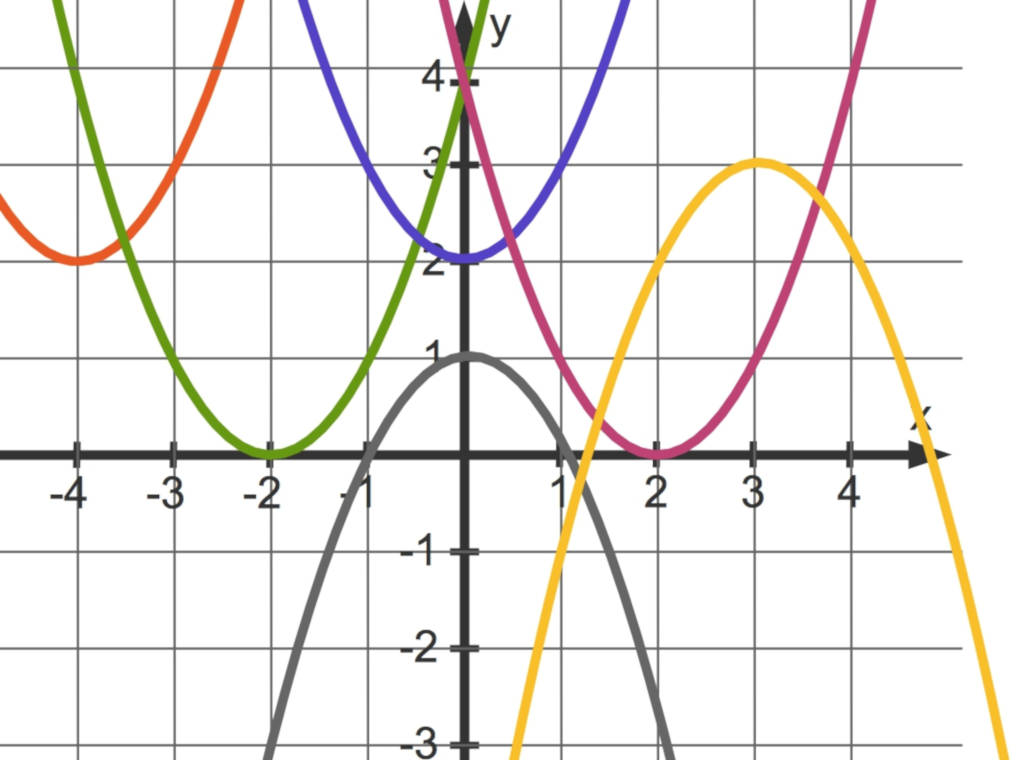
Kannst du erraten, wo die extremsten Werte der Parabeln sind? Ganz genau – jeweils im Scheitelpunkt. Wie du siehst, können Parabeln nach oben oder nach unten geöffnet sein. Die $y$-Koordinate des Scheitelpunkts ist daher entweder der größte oder der kleinste Wert der Funktion. Aber auf jeden Fall ziemlich extrem. Das war ja einfach!
Beispiel einer Extremwertaufgabe mit quadratischer Funktion
Jetzt wird’s ernst. Du kennst jetzt die Theorie. Auf in die Praxis: Stell dir vor, deine Mutter hat einen $12\ \text{m}$ langen Zaun für euer neues Kaninchengehege gekauft. Du möchtest, dass die Kaninchen möglichst viel Auslauffläche $A$ im Garten haben sollen. Deshalb überlegst du dir, die Rückwand von der Garage deines Nachbarn zu nutzen. Weil er nett ist, hat er nichts dagegen! Auch deine Mutter findet die Idee super und meint, du solltest einfach ein rechteckiges Gehege mit dem Zaun und der Wand bauen. Die Länge $y$ und Breite $x$ des Rechtecks kann sie dir aber nicht sagen.
Kannst du die optimalen Maße des Auslaufs bestimmen? Folgende Bedingungen musst du dabei beachten:
$ 12\ \text{m} = x+x+y\\ A = x\cdot y $
Wenn du die Gleichungen ineinander einsetzt, erhältst du eine quadratische Funktion. Mit der quadratischen Ergänzung kannst du dann den Scheitelpunkt bestimmen.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Extremwertaufgaben mit quadratischen Funktionen (2 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Extremwertaufgaben mit quadratischen Funktionen (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter



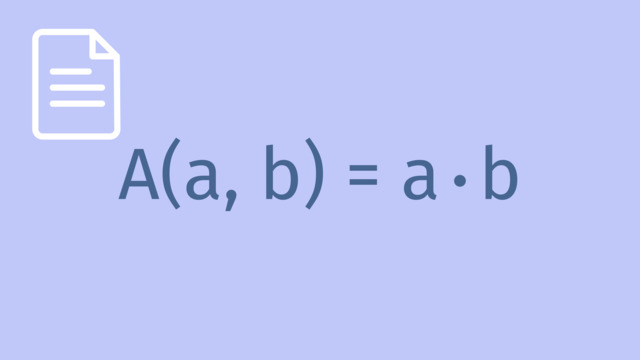



 Die Ziege – Extremwertaufgabe mit quadratischer Funktion
Die Ziege – Extremwertaufgabe mit quadratischer Funktion
 Extremwertaufgaben mit quadratischen Funktionen – Anleitung
Extremwertaufgaben mit quadratischen Funktionen – Anleitung












