Dreisatz
Der Dreisatz ist ein Verfahren, mit dem man bei proportionalen oder anti-proportionalen Verhältnissen unbekannte Größen bestimmen kann.
Beliebteste Videos
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Wann wird der Dreisatz verwendet?
- Der Zweisatz
- Proportionale Zuordnungen
- Antiproportionale Zuordnungen
- Darstellung von proportionalen oder antiproportionalen Zuordnungen als Funktionsgleichung
Wann wird der Dreisatz verwendet?
Der Dreisatz ist ein häufig verwendetes Rechenverfahren in der Mathematik. Bei gegebenen Zusammenhängen oder Beziehungen zwischen Größen soll eine fehlende Größe berechnet werden.
Beispiel
Du gehst einkaufen und findest deine Lieblingsmarmelade. Diese kostet $2,80~€$ für $350~g$.
- Du möchtest nun wissen, wie viel ein Kilogramm deiner Lieblingsmarmelade kostet.
- Oder: In einem Extraständer steht diese Marmelade als Sonderangebot: $1,80~€$ für $200~g$. Ist dies wirklich günstiger?
Solche Aufgaben kannst du mit dem Dreisatz rechnen.
Übrigens: Nur wenige Menschen haben Lust, den Dreisatz beim Einkaufen zu üben. Deshalb ist der Handel verpflichtet, zur besseren Vergleichbarkeit der Preise diese immer in $100~g$ oder $1000~g$ anzugeben.
Der Zweisatz
Beim Zweisatz ist ein Wert für eine Basiseinheit angeben. Dieser Wert muss dann noch entsprechend multipliziert werden.
Wenn zum Beispiel ein Brot $2,60~€$ kostet, was kosten dann drei Brote?
- $2,60~€$ ist der Basispreis für ein Brot.
- Da mehrere Brote mehr kosten als nur ein Brot, muss dieser Preis mit der entsprechenden Anzahl multipliziert werden.
- Drei Brote kosten somit $3\cdot 2,60~€=7,80~€$.
Wenn der Wert für eine Basiseinheit nicht gegeben ist, muss dieser zunächst ermittelt werden. Dies führt zu dem Dreisatz.
Proportionale Zuordnungen
Bei den obigen Beispielen mit dem Brot und auch mit der Lieblingsmarmelade gilt, dass die Erhöhung (Verringerung) der Menge zu einer Erhöhung (Verringerung) des Preises führt. Dies bedeutet entweder
- je mehr, desto mehr oder
- je weniger, desto weniger.
Eine solche Zuordnung kennst du als proportionale Zuordnung oder auch direkt proportionale Zuordnung.
Beispiel
Du kannst diese Rechnung wie folgt durchführen:
- Du notierst die gegebenen Werte: Bei dem Beispiel mit der Lieblingsmarmelade entspricht dem Gewicht $350~g$ der Preis $2,80~€$. Dies wird so geschrieben: $350~g~\hat =~2,80~€.$
- Dann berechnest du den Preis einer Basisgröße. Diese könnte $100~g$ oder auch $1~g$ sein.
- Da es sich um eine direkt proportionale Zuordnung handelt, teilst du die $350~g$ durch $3,5$. So kommst du auf $100~g$. Ebenso teilst du $2,80~€$ durch $3,5$. So kommst du auf den entsprechenden Preis und erhältst: $100~g~\hat=~0,80~€.$
- Da der Preis von einem Kilogramm der Marmelade gefragt ist, also $1000~g$, wird die Basisgröße und ebenso der Preis mit $10$ multipliziert.
Dies kannst du auch in einer Tabelle darstellen. Dabei stehen im Kopf der Tabelle die Größen, die in einer Beziehung zueinander stehen. Zum Beispiel Gewicht und Preis.:
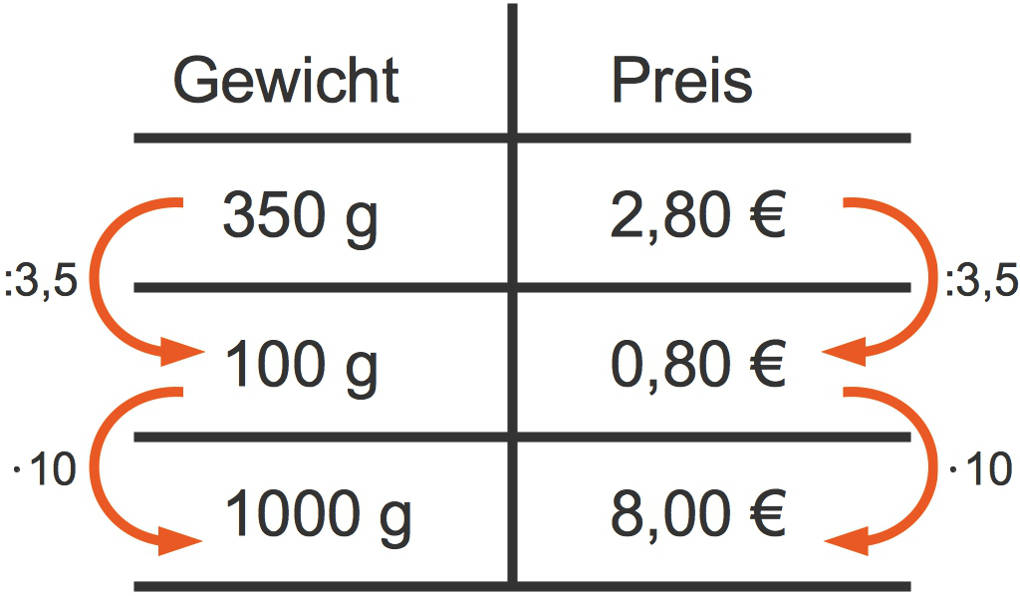
$1000~g$ der Lieblingsmarmelade kosten also $8~€$.
Du siehst es wird auf beiden Zahlen entweder durch die gleiche Zahl dividiert oder mit der gleichen Zahl multipliziert.
Durch Multiplikation der Basisgröße mit $2$ kannst du auch prüfen, ob das sogenannte Sonderangebot wirklich eines ist. $200~g$ der Marmelade kosten $2\cdot 0,80~€=1,60~€$. Das angepriesene Sonderangebot ist also keines, da der ausgewiesene Sonderpreis $1,80~€$ höher ist als der ursprüngliche, $1,60~€$.
Prozentrechnung
Auch bei der Prozentrechnung kann der Dreisatz zur Anwendung kommen. Du kannst Aufgaben mit dem Dreisatz berechnen – Hier ein Beispiel:
Du hast $200~€$ gespart und erhältst $3,5~\%$ Zinsen darauf. Du kennst also den Grundwert ($200~€$) und den Prozentsatz ($3,5~\%$). Gesucht ist der Prozentwert, also das Geld, welches du nach einem Jahr an Zinsen erhältst.
- $200~€~\hat = ~100~\%$.
- Indem du durch $100$ dividierst, erhältst du $2~€~\hat =~1~\%$.
- Nun multiplizierst du mit $3,5$ und erhältst $7~€~\hat =~3,5~\%$.
$3,5~\%$ von $200~€$ sind somit $7~€$.
Antiproportionale Zuordnungen
Möchtest du zusammen mit einigen Mitschülern euer Klassenzimmer neu streichen, benötigt ihr zu viert $6$ Stunden. Wie lange braucht ihr, wenn ihr zu sechst seid? Je mehr Schüler bei der Arbeit helfen, umso weniger Zeit benötigt ihr.
Dieses Mal gilt, dass die Erhöhung (Verringerung) der Anzahl der Schüler zu einer Verringerung (Erhöhung) der Zeit führt. Dies bedeutet entweder
- je mehr, desto weniger oder
- je weniger, desto mehr.
Eine solche Zuordnung kennst du als antiproportionale Zuordnung oder auch indirekt proportionale Zuordnung.
Beispiel
Auch bei antiproportionalen Zuordnungen führst du die Berechnungen in einer Tabelle durch.
- Dabei stehen im Kopf der Tabelle die Größen, die in einer Beziehung zueinander stehen. Zum Beispiel Anzahl der Schüler und die Zeit.
- Dann notierst du die gegebenen Werte.
- Dann berechnest du die Zeit, die ein Schüler für die Arbeit benötigt.
- Da es sich um eine antiproportionale Zuordnung handelt, teilst du die die Anzahl der Schüler, also $4$, durch $4$. Die benötigte Zeit multiplizierst du mit $4$ und erhältst $24$ Stunden.
- Nun multiplizierst du die Zahl der Schüler mit $6$ und dividierst die Stunden durch $6$.
Dies siehst du hier in der Tabelle:
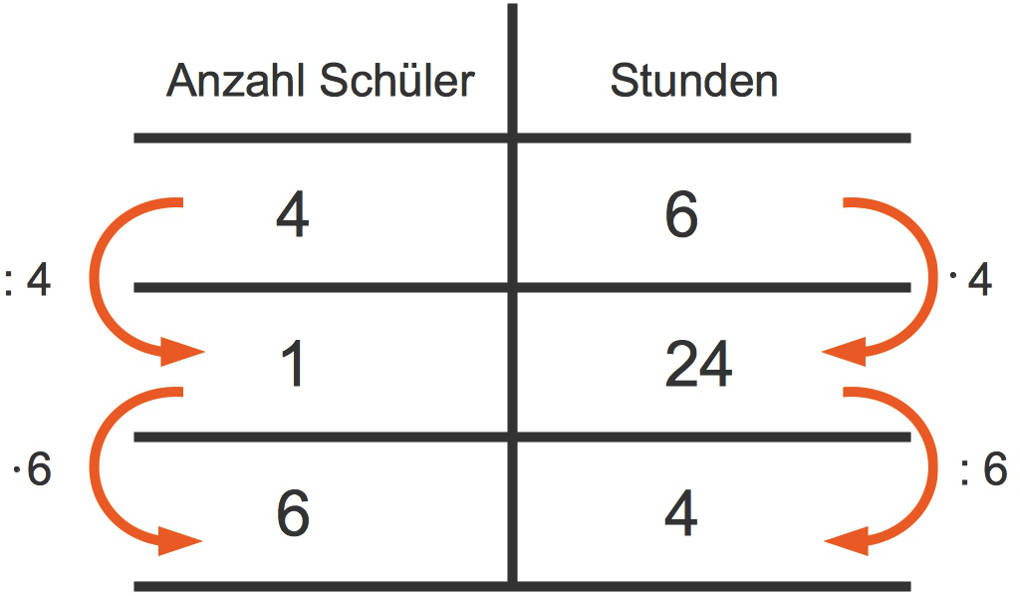
Sechs Schüler benötigen also $4$ Stunden für die Arbeit.
In dieser Tabelle siehst du, dass auf der einen Seite durch eine Zahl dividiert, auf der anderen jedoch mit dieser Zahl multipliziert wird oder umgekehrt.
Dreisatz bei proportionalen und antiproportionalen Zuordnungen kommt vor allem bei Textaufgaben und Alltagsproblemen vor.
Darstellung von proportionalen oder antiproportionalen Zuordnungen als Funktionsgleichung
Wenn du dir Beispiele zum Dreisatz, wie die beiden obigen Tabellen, anschaust, fällt dir auf, dass
- bei proportionalen Zuordnungen der Quotient der Größen immer gleich ist. Dies wird als Quotientengleichheit bezeichnet.
- bei antiproportionalen Zuordnungen das Produkt immer übereinstimmt. Dies wird als Produktgleichheit bezeichnet.
Damit können sowohl bei proportionalen als auch bei antiproportionalen Zuordnungen Funktionsgleichungen aufgestellt werden, welche den Zusammenhang zwischen den betrachteten Größen darstellen.
Beispiel „Marmelade“
Es gilt $2,80~:~3,5=0,8$. Dies ist gerade der Preis für $100~g$ Marmelade. Ebenso gilt $8~:~10=0,8$. Umgekehrt kann man daraus folgern, dass der Preis $y$ für $x\cdot 100~g$ Marmelade sich ergibt durch die Gleichung
$y=0,8\cdot x$ .
Dies ist die Gleichung einer proportionalen Funktion.
Nun kannst du zu jeder beliebigen Menge $x$, in $100~g$, den zugehörigen Preis, in $€$, bestimmen.
Beispiel „Aufgaben zum Dreisatz“
Bei antiproportionalen Zuordnungen stimmen die jeweiligen Produkte überein:
- $6\cdot 4=24$
- $1\cdot 24=24$
- $4\cdot 6=24$
Das bedeutet, dass allgemein $x\cdot y=24$. Teilst du durch $x$, so erhältst du
$y=\frac{24}x$.
Dies ist die Gleichung einer antiproportionalen Funktion.
Alle Videos zum Thema
Videos zum Thema
Dreisatz (6 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Dreisatz (6 Arbeitsblätter)
-
 Wie löse ich Aufgaben mit dem Dreisatz?
PDF anzeigen
Wie löse ich Aufgaben mit dem Dreisatz?
PDF anzeigen -
 Dreisatz bei proportionalen und antiproportionalen Zuordnungen
PDF anzeigen
Dreisatz bei proportionalen und antiproportionalen Zuordnungen
PDF anzeigen -
 Dreisatz bei proportionalen Zuordnungen – Beispiele
PDF anzeigen
Dreisatz bei proportionalen Zuordnungen – Beispiele
PDF anzeigen -
 Dreisatz bei antiproportionalen Zuordnungen – Beispiele
PDF anzeigen
Dreisatz bei antiproportionalen Zuordnungen – Beispiele
PDF anzeigen -
 Dreisatz bei Textaufgaben – proportional oder antiproportional?
PDF anzeigen
Dreisatz bei Textaufgaben – proportional oder antiproportional?
PDF anzeigen -
 Zusammengesetzter Dreisatz
PDF anzeigen
Zusammengesetzter Dreisatz
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Brüche multiplizieren – Übungen
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen





















