Scharen von Winkelfunktionen

Inhaltsverzeichnis zum Thema

• Einleitung
• Winkelfunktionen
• Eigenschaften der Sinusfunktion
• Funktionenscharen
• Scharen von Winkelfunktionen
• Welche Bedeutung hat der Parameter $a$?
• Welche Bedeutung hat der Parameter $b$?
• Welche Bedeutung haben die Parameter $d$ sowie $e$?
• Verschiebung entlang der $x$-Achse
• Verschiebung entlang der $y$-Achse

Einleitung

Zunächst klären wir die Begriffe Winkelfunktion sowie Funktionenscharen.

Winkelfunktionen

Eine Winkelfunktion ist eine Funktion $f$, in deren Funktionsterm Sinus, Cosinus oder Tangens vorkommen. Im Folgenden schauen wir uns dies am Beispiel des Sinus ein wenig genauer an.

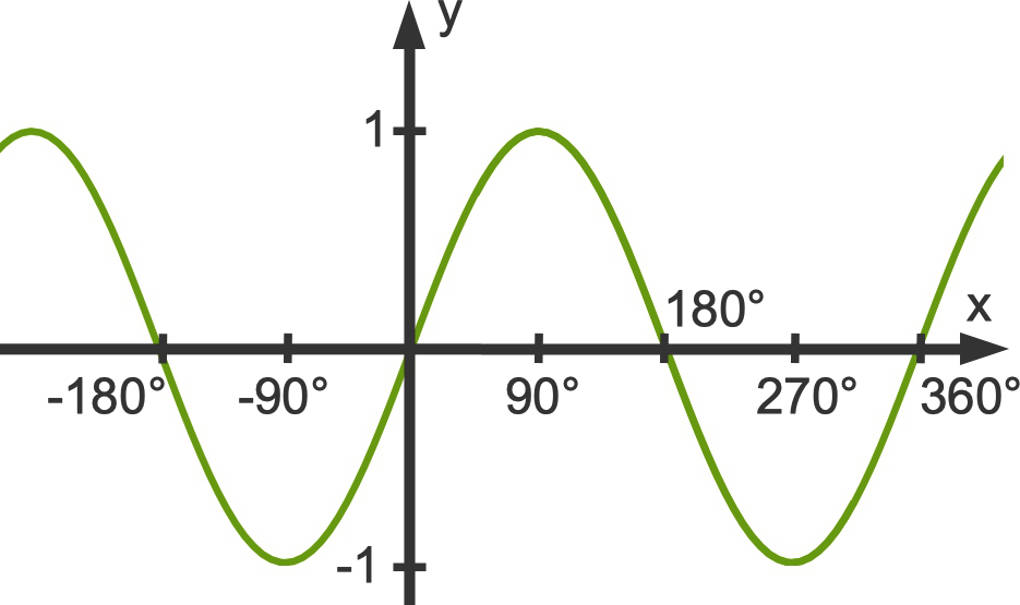
Eigenschaften der Sinusfunktion

Zunächst lernst du noch einige wichtige Eigenschaften der Sinusfunktion kennen:

• Der Definitionsbereich ist $\mathbb{D}=\mathbb{R}$, also die Menge der reellen Zahlen.
• Der Wertebereich ist $\mathbb{W}=[-1;1]$.
• Die Sinusfunktion ist periodisch mit der Periode $360^{\circ}$ im Winkelmaß beziehungsweise $2\pi$ im Bogenmaß.
• Die Nullstellen der Sinusfunktion sind die ganzzahligen Vielfachen von $180^{\circ}$ beziehungsweise $\pi$.
• Die Sinusfunktion ist punktsymmetrisch zum Koordinatenursprung.
• Die Hälfte der Differenz von maximalem und minimalem Funktionswert $0,5\cdot(1-(-1))=1$ wird als Amplitude der Sinusfunktion bezeichnet.

Funktionenscharen

Wenn in einer Funktion neben der Variablen $x$ noch ein Parameter vorkommt, spricht man von einer Funktionenschar.

Scharen von Winkelfunktionen

In einer Winkelfunktion können Parameter vorkommen: Hierfür untersuchen wir nun die Funktion $f$ mit

$f(x)=a\cdot \sin(b(x−d))+e$.

Im Folgenden wird immer die Wirkung eines Parameters betrachtet. Die übrigen Parameter sind dann fest.

Bei den jeweiligen Funktionsgraphen ist auf der $x$-Achse das Bogenmaß eingezeichnet. Dabei kannst du den Bogenmaßen folgende Winkelmaße zuordnen:

• $0~\hat =~0^{\circ}$
• $\frac{\pi}2~\hat =~90^{\circ}$
• $\pi~\hat =~180^{\circ}$
• $\frac{3\pi}2~\hat =~270^{\circ}$
• $2\pi~\hat =~360^{\circ}$

Welche Bedeutung hat der Parameter $a$?

Es sind $b=1$ sowie $d=e=0$. Wir betrachten also die Schar von Winkelfunktionen $f_{a}$ mit $f_{a}(x)=a\cdot \sin(x)$.

Wenn du die Sinusfunktion mit einem Faktor $a\neq 0$ multiplizierst, ändert sich der Wertebereich und auch die Amplitude.

Der Wertebereich ist dann $[-|a|;|a|]$ und die Amplitude $|a|$.

Die Periode und auch die Symmetrie ändern sich nicht.

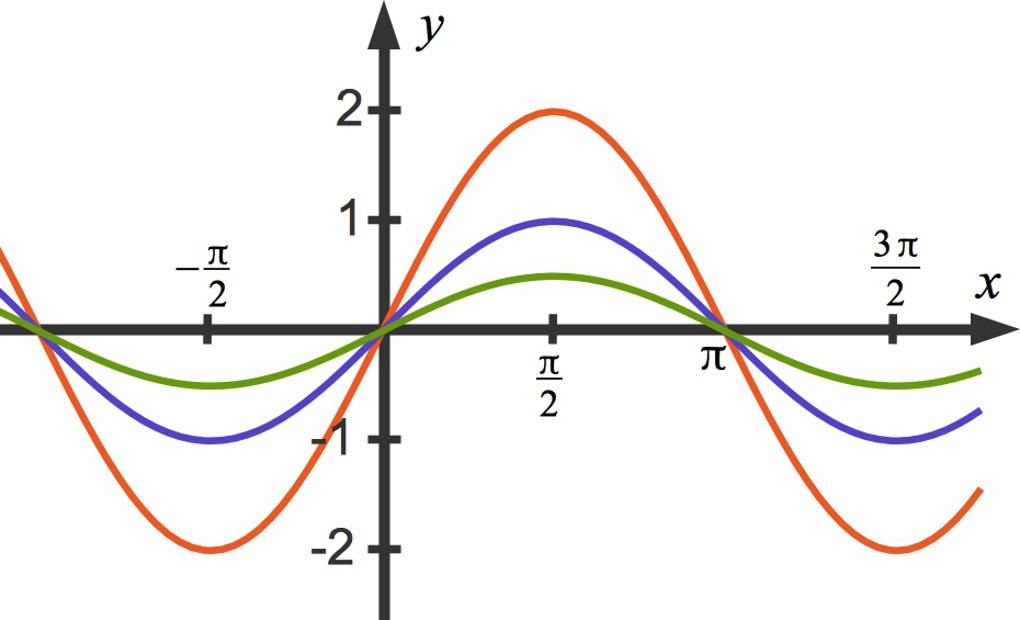
Der blaue Funktionsgraph gehört zu $a=1$, der grüne zu $a=\frac12$ und der rote zu $a=2$.

Welche Bedeutung hat der Parameter $b$?

Diesmal sind $a=1$ sowie $d=e=0$. So betrachten wir also die Schar von Winkelfunktionen $f_{b}$ mit $f_{b}(x)=\sin(bx)$.

In diesem Fall ändern sich weder der Wertebereich noch die Amplitude jedoch die Periode: Es gilt allgemein für die Periode $P=\frac{360^{\circ}}{|b|}$.

Das bedeutet graphisch:

• Der Funktionsgraph wird gestreckt entlang der $x$-Achse für $|b|\lt 1$ und gestaucht für $|b|\gt 1$. Man spricht in diesem Zusammenhang auch von der Frequenz.
• Für $b\lt 0$ wird der Funktionsgraph an der $x$-Achse gespiegelt.

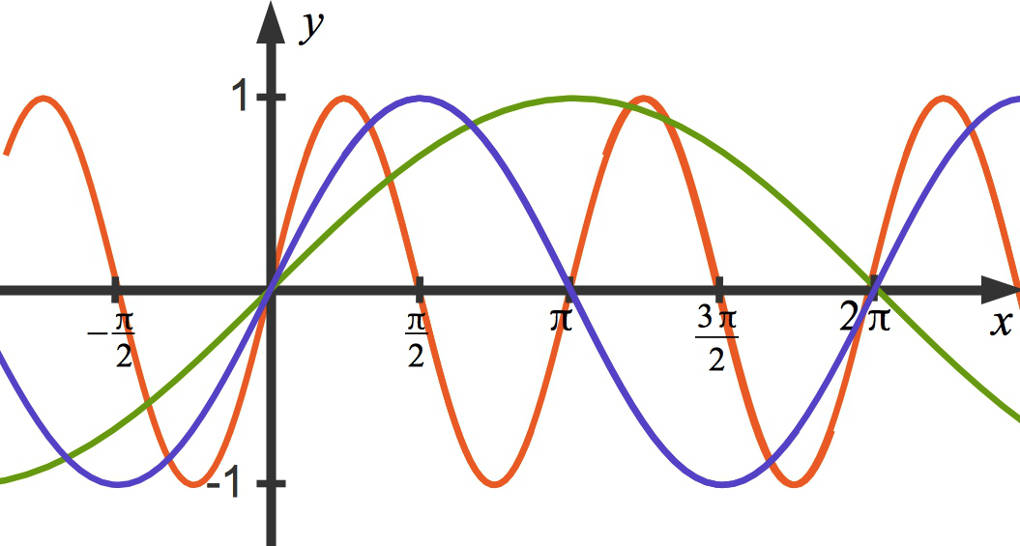
Der blaue Funktionsgraph gehört zu $b=1$, der grüne zu $b=\frac12$ und der rote zu $b=2$.

Welche Bedeutung haben die Parameter $d$ sowie $e$?

Du siehst, die beiden Parameter $a$ sowie $b$ führen zu Streckungen beziehungsweise Stauchungen des Funktionsgraphen. Nun schauen wir uns noch die beiden verbleibenden Parameter an: Zuletzt sind $a=b=1$. So kommen wir zu den Scharen von Winkelfunktionen

• $f_{d}(x)=\sin(x−d)$ für $e=0$ sowie
• $f_{e}(x)=\sin(x)+e$ für $d=0$.

Verschiebung entlang der $x$-Achse

Der Parameter $d$ bewirkt eine Verschiebung der Sinusfunktion um $d$ Einheiten in positiver Richtung entlang der $x$-Achse.

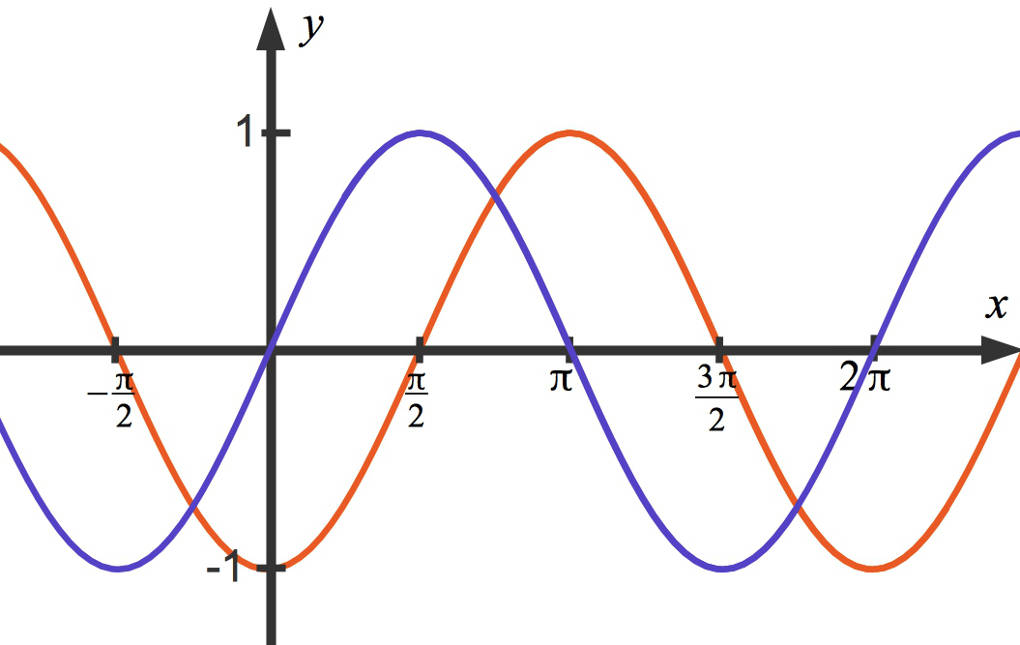
Der blaue Funktionsgraph gehört zu $d=0$ und der rote zu $d=\frac{\pi}2$, das entspricht im Winkelmaß $180^{\circ}$.

Verschiebung entlang der $y$-Achse

Der Parameter $e$ bewirkt eine Verschiebung der Sinusfunktion um $e$ Einheiten in positiver Richtung entlang der $y$-Achse.

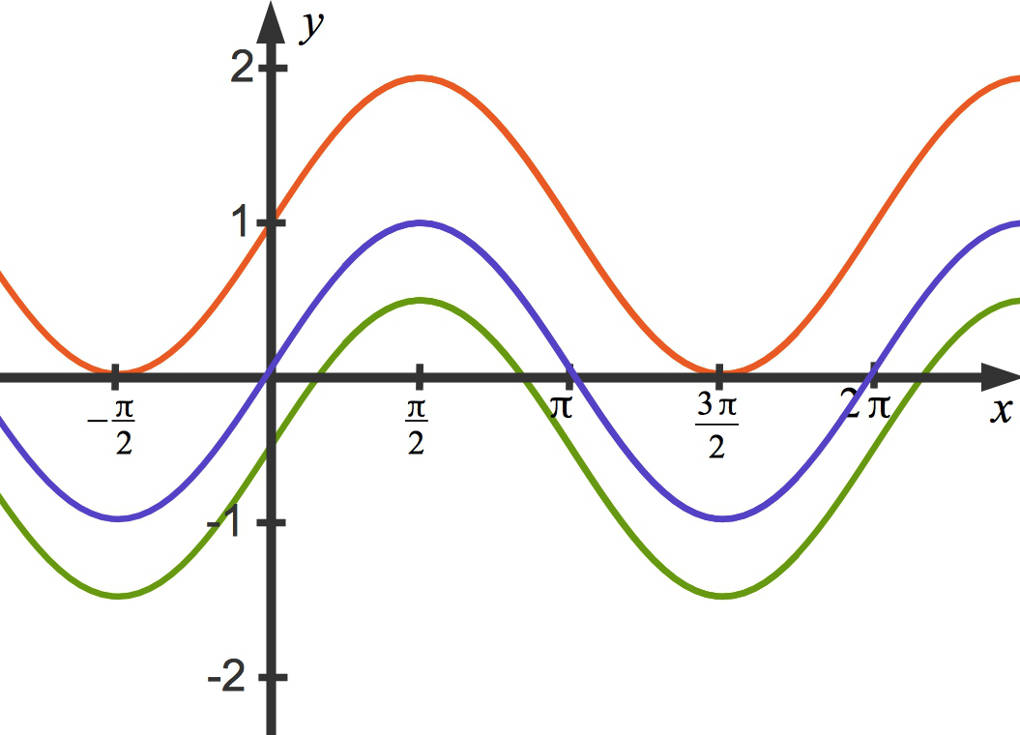
Der blaue Funktionsgraph gehört zu $e=0$, der rote zu $e=1$ und der grüne zu $e=-0,5$.