Scharen von Exponential- und Logarithmusfunktionen
Definitionsbereich, Wertebereich, Nullstellen, Symmetrie, Extrema, Wendepunkte, Verhalten im Unendlichen, Schnittpunkt y-Achse, Sattelpunkte, Graph, Parameter
Beliebteste Videos
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Exponential- und Logarithmusfunktion
- Scharen von Exponentialfunktionen
- Definitionsmenge
- Wertemenge
- Symmetrien
- Schnittpunkte mit den Koordinatenachsen
- Extrema
- Grenzwerte
Exponential- und Logarithmusfunktion
Zunächst sollst du die wichtigsten Eigenschaften von Exponentialfunktionen und Logarithmusfunktionen wiederholen.
Sieh dir dazu folgende Exponentialfunktion an:
$f(x)=b^x$
Dabei ist $x$ die Variable und es gelte $b\gt 0$ und $b\neq 1$.
Beachte: Egal was du für $x$ einsetzt, der Wert der Funktion ist immer echt größer $0$.

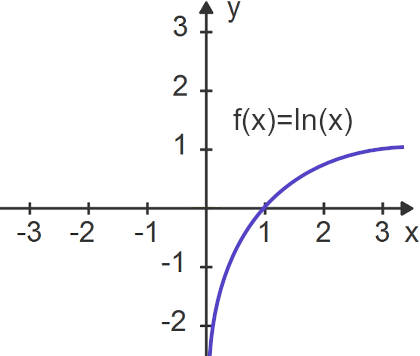
Betrachte nun folgende Logarithmusfunktion:
$f(x)=log_b(x)$
Auch hier ist $x$ die Variable und es gelte $b\gt 0$ und $b\neq 1$. Die Logarithmusfunktion ist die sogenannte Umkehrfunktion der Exponentialfunktion. Die Wertemenge von $b^x$ ist deshalb die Definitionsmenge von $log_b(x)$.
Beachte: Du darfst für $x$ in die Logarithmusfunktion nur Zahlen echt größer $0$ einsetzen.
Scharen von Exponentialfunktionen
Du kennst jetzt die wichtigsten Eigenschaften von Exponential- und Logarithmusfunktionen. Nun lernst du, wie du Scharen von Exponentialfunktionen in einer Kurvendiskussion löst:
$f_a(x)=ax\cdot e^x$
$g_a(x)=5^x\cdot (a-x)$
$k_a(x)=x^2\cdot e^{ax}$
Alle diese Funktionen hängen vom Scharparameter $a$ ab und enthalten eine Exponentialfunktion.
Die Beispiele sehen für dich furchteinflößend aus? Keine Bange, du kannst alle Methoden, die du bei einfacheren Funktionen gelernt hast, trotzdem anwenden. Behandle den Parameter $a$ einfach so, als wäre dieser eine normale Zahl.
Betrachte nun folgendes Beispiel:
$h_a(x)=(x-1)\cdot e^{ax}\quad\text{mit}\quad a\neq 0$
Definitionsmenge
Die Funktion ist ein Produkt. Dieses besteht aus dem linearen Faktor $(x-1)$ und der Exponentialfunktion $e^{ax}$. Sowohl in den linearen Faktor als auch in die Exponentialfunktion darfst du für $x$ alle Zahlen einsetzen. Die Definitionsmenge für das Produkt ist deshalb auch $\mathbb{R}$.
Wertemenge
Die Exponentialfunktion $e^{ax}$ ist immer positiv. Der lineare Faktor kann allerdings alle Werte aus $\mathbb{R}$ annehmen. Deshalb ist die Wertemenge auch ganz $\mathbb{R}$.
Mit einer Kurvendiskussion kannst du die Funktion noch besser kennenlernen.
Symmetrien
Untersuche, ob der Graph von $h_a(x)$ eine Achsensymmetrie oder eine Punktsymmetrie aufweist. Überprüfe hierzu zunächst die Bedingung für die Achsensymmetrie, also ob $h_a(-x)=h_a(x)$ gilt:
$\begin{array}{lllll} h_a(-x) &=& ((-x)-1)\cdot e^{a(-x)} \\ &=& (-x-1)\cdot e^{-ax} \\ &\neq& h_a(x) \end{array}$
Da die Funktion nicht achsensymmetrisch ist, überprüfst du nun die Bedingung für die Punktsymmetrie. Du zeigst also, ob $-h_a(-x)=h_a(x)$ ist:
$\begin{array}{lllll} -h_a(-x) &=& -((-x)-1)\cdot e^{a(-x)} \\ &=& (x+1)\cdot e^{-ax} \\ &\neq& h_a(x) \end{array}$
Der Graph ist also weder achsensymmetrisch zur $y$-Achse noch punktsymmetrisch zum Ursprung.
Schnittpunkte mit den Koordinatenachsen
Als nächstes kannst du die Schnittpunkte mit den Koordinatenachsen berechnen. Diese helfen dir beim Skizzieren des Graphen.
Für die Schnittpunkte mit der $x$-Achse bzw. den Nullstellen musst du $y$ bzw. $h_a(x)$ gleich $0$ setzen:
$ \begin{array}{rcl} 0 &=& (x-1)\cdot e^{ax}\\ 0 &=& (x-1) \\ x &=& 1 \\ \end{array} $
Der Satz vom Nullprodukt besagt, dass ein Produkt $0$ wird, wenn einer der Faktoren $0$ ist. Die Exponentialfunktion kann nicht $0$ werden, deshalb betrachtest du nur den Faktor $(x-1)$. Wir erhalten somit den Schnittpunkt mit der $x$-Achse $N(1|0)$.
Für die Schnittpunkte mit der $y$-Achse setzt du dagegen für $x$ gleich $0$ ein:
$h_a(0) = (0-1)\cdot e^{a\cdot 0} = -1 \cdot 1 = -1$
Der Funktionsgraph schneidet die $y$-Achse also im Punkt $S_y(0|-1)$.
Extrema
Für die Berechnung der Extrempunkte benötigen wir die erste und die zweite Ableitung von $h_a(x)$. Diese kannst du mit der Produktregel bilden:
$ \begin{array}{rcl} h_a(x) &=& (x-1)\cdot e^{ax}\\ h^\prime_a(x) &=& 1\cdot e^{ax} + (x-1)\cdot ae^{ax}\\ &=& (1+ax-a)\cdot e^{ax}\\ \end{array} $
$ \begin{array}{rcl} h^{\prime\prime}_a(x) &=& a\cdot e^{ax} + (1+ax -a)\cdot ae^{ax}\\ &=& (2a + a^2x-a^2)\cdot e^{ax}\\ \end{array} $
Ein notwendiges Kriterium für Extrempunkte ist, dass die erste Ableitung gleich $0$ ist:
$ \begin{array}{rcl} (1+ax-a)\cdot e^{ax} &=& 0\\ 1+ax-a &=& 0 \\ ax &=& a-1 \\ x &=& \frac{a-1}{a} \\ \end{array} $
Welche Art von Extremum vorliegt, kannst du feststellen, indem du diesen $x$-Wert in die zweite Ableitung einsetzt:
$ \begin{array}{rcl} h^{\prime\prime}_a(\frac{a-1}{a}) &=& (2a + a^2\cdot(\frac{a-1}{a}) -a^2)\cdot e^{a\cdot(\frac{a-1}{a})}\\ &=& a\cdot e^{a-1} \\ \end{array} $
Je nachdem, welchen Wert $a$ annimmt, handelt es sich um einen Tiefpunkt, Sattelpunkt oder Hochpunkt des Graphen:
$ \begin{array}{rcl} a\cdot e^{a-1} &\gt & 0 & \text{für} & a\gt 0 & \Rightarrow \text{Tiefpunkt}\\ a\cdot e^{a-1} &=& 0 & \text{für} & a=0 & \Rightarrow \text{Sattelpunkt}\\ a\cdot e^{a-1} &\lt & 0 & \text{für} & a\lt 0 & \Rightarrow \text{Hochpunkt}\\ \end{array} $
Da $a\neq 0$ festgelegt ist, kann es sich nur um einen Hoch- oder Tiefpunkt handeln.
Grenzwerte
Auch die Grenzwerte unserer Beispielfunktion $h_a(x)$ berechnen sich wie üblich. Allerdings musst du zwei Fälle unterscheiden:
Wenn $a\gt 0$ ist, dann gilt:
$\lim\limits_{x \rightarrow \infty}{(x-1)\cdot e^{ax}} \rightarrow \infty$
$\lim\limits_{x \rightarrow -\infty}{(x-1)\cdot e^{ax}} = 0$
Wenn $a\lt 0$ ist, dann gilt:
$\lim\limits_{x \rightarrow \infty}{(x-1)\cdot e^{ax}} = 0$
$\lim\limits_{x \rightarrow -\infty}{(x-1)\cdot e^{ax}} \rightarrow -\infty$
Scharen von Logarithmusfunktion
Genauso, wie vorher bei der Exponentialfunktion gibt es Logarithmusfunktionen, die von einem Scharparameter abhängen:
$f_a(x)= x\cdot ln(ax)$
$g_a(x)= \frac{ln(x^2)}{x^a}$
$h_a(x)= 2x\cdot log_6(x+a)$
Auch hier kannst du so rechnen, als wäre der Scharparameter $a$ eine normale Zahl. Alle grundsätzlichen Vorgehensweisen bei den Berechnungen, wie z.B. bei der Kurvendiskussion, bleiben unverändert.
Alle Videos zum Thema
Videos zum Thema
Scharen von Exponential- und Logarithmusfunktionen (3 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Scharen von Exponential- und Logarithmusfunktionen (3 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Schriftliche Division – Übungen
- Meter








 Scharen von Exponentialfunktionen – Kurvendiskussion (1)
Scharen von Exponentialfunktionen – Kurvendiskussion (1)
 Scharen von Exponentialfunktionen – Kurvendiskussion (2)
Scharen von Exponentialfunktionen – Kurvendiskussion (2)
 Scharen von Logarithmusfunktionen – Kurvendiskussion
Scharen von Logarithmusfunktionen – Kurvendiskussion












