Ableitung einer Funktion an einer Stelle: f '(xₒ)
lokale Änderungsrate, Momentangeschwindigkeit, Differentialquotient, x gegen x Null, h gegen Null, h-Methode, x-0-Methode
Inhaltsverzeichnis zum Thema
- Von der mittleren Änderungsrate zur lokalen Änderungsrate
- Bestimmen der lokalen Änderungsrate
- Termumformung
- h-Methode
- Testeinsetzen
Von der mittleren Änderungsrate zur lokalen Änderungsrate
Die mittlere Änderungsrate einer Funktion auf einem Intervall $[a;b]$ ist die Steigung einer Sekante. Diese Sekante verläuft durch zwei Punkte $P(a|f(a))$ sowie $Q(b|f(b))$ des Funktionsgraphen.
Dies schauen wir uns einmal an einem Beispiel an: $f(x)=x^{2}-2$ mit dem Intervall $[0;2]$.
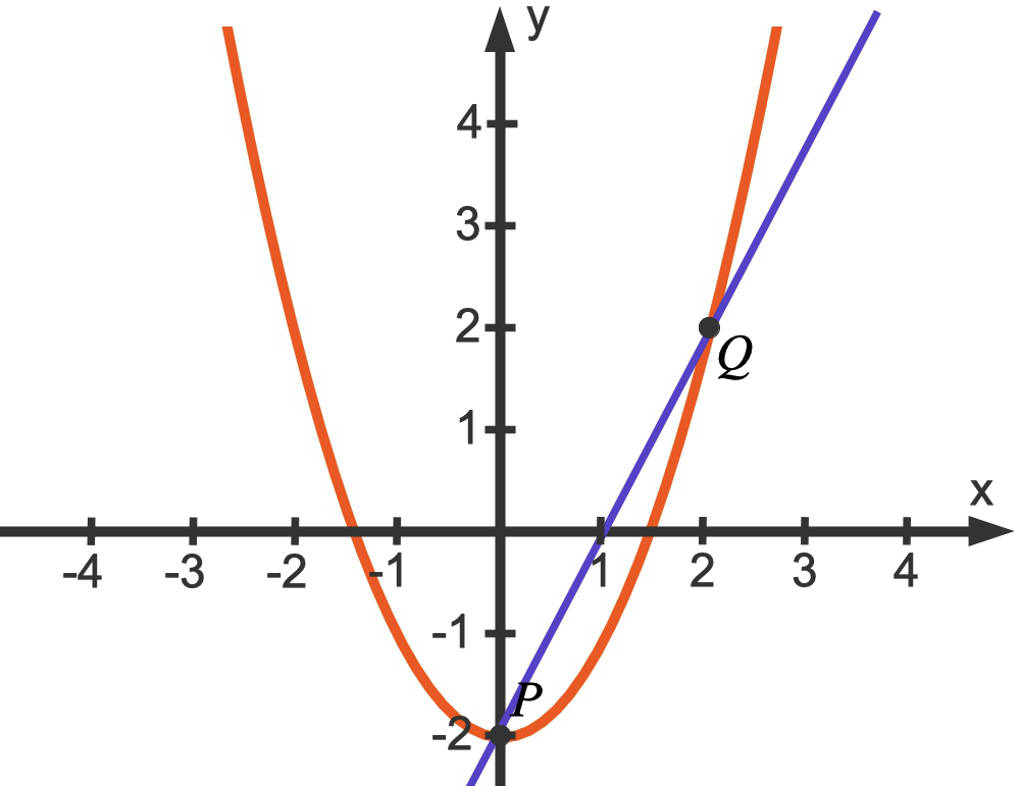
Die Steigung der blau eingezeichneten Sekante kannst du mit Hilfe des Differenzenquotienten bestimmen:
$m=\frac{f(2)-f(0)}{2-0}=\frac{2-(-2)}{2}=\frac42=2$
Die lokale Änderungsrate ist die Steigung einer Tangente. Wie kommst du zu dieser Tangente?
Stell dir das so vor: Die mittlere Änderungsrate ist die Steigung der Sekante durch die Punkte $P(a|f(a))$ und $Q(b|f(b))$ des Funktionsgraphen von $f$. Du lässt nun einen der beiden Punkte, zum Beispiel $P(a|f(a))$, entlang des Funktionsgraphen gegen den Punkt $Q(b|f(b))$ wandern. So erhältst du viele Sekanten. Im Grenzwert $\lim\limits_{a\to b}$ erhältst du die (hier grün eingezeichnete) Tangente an den Funktionsgraphen in dem Punkt $Q(b|f(b))$. Deren Steigung wird als lokale Änderungsrate oder auch Steigung der Funktion in dem Punkt $Q$ bezeichnet.
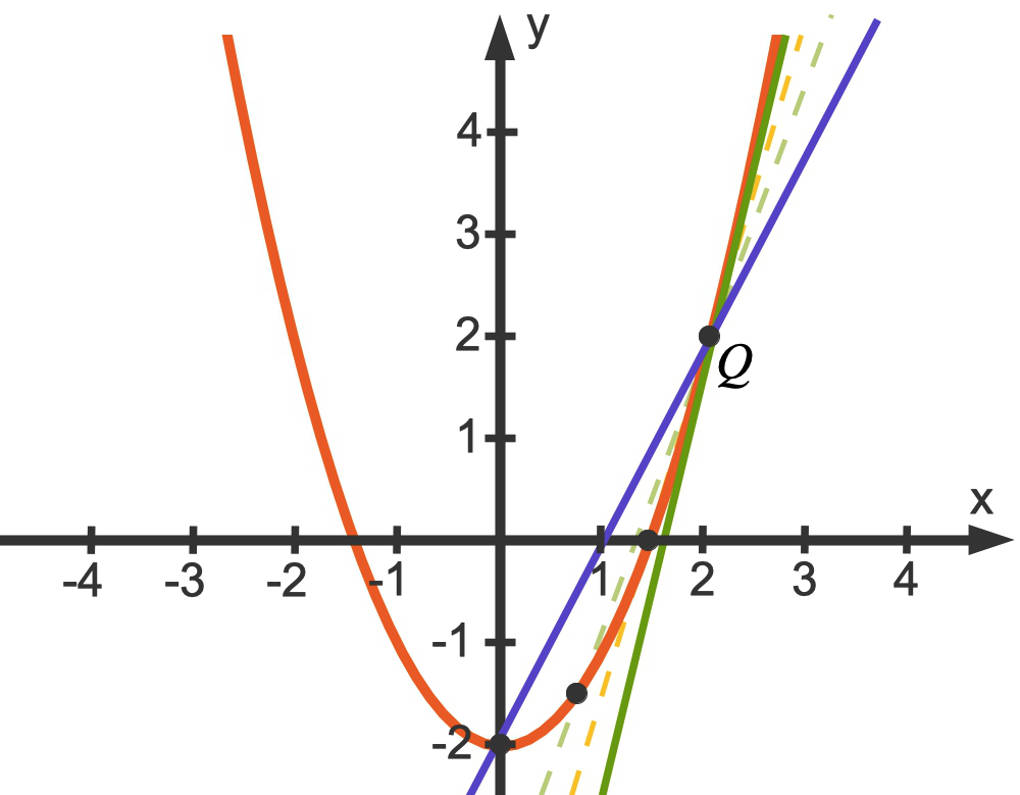
Bestimmen der lokalen Änderungsrate
Nun kommen wir zu der lokalen Änderungsrate einer Funktion $f$ an der Stelle $x_{0}$. Diese wird mit $f'\left(x_0\right)$ bezeichnet. Du erhältst diese durch Grenzwertbildung der mittleren Änderungsrate:
$f'\left(x_0\right)=\lim\limits_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0} $
Der Term rechts von dem Gleichheitszeichen wird als Differentialquotient bezeichnet.
Schließlich lernst du noch, wie du den Grenzwert berechnen kannst und somit die Ableitung einer Funktion $f$ an einer Stelle $x_{0}$.
Einen Überblick über die im Folgenden kurz aufgezeigten Verfahren findest du bei Grenzwerte $x$ gegen $x_{0}$.
Wir betrachten jedes der dargestellten Verfahren an dem Beispiel der Funktion $f$ mit $f(x)=x^{2}-2$ und $x_{0}=2$.
Termumformung
Du musst den folgenden Grenzwert berechnen:
$f'\left(2\right)=\lim\limits_{x\to 2} \frac{f(x)-f(2)}{x-2}=\lim\limits_{x\to 2}\frac{x^2-2-(2^2-2)}{x-2}=\lim\limits_{x\to 2}\frac{x^2-4}{x-2} $
Bei der Termumformung verwendest du entweder die binomischen Formeln oder die Polynomdivision.
Auf den Term im Zähler kannst du die 3. binomische Formel anwenden: $x^{2}-4=(x+2)\cdot (x-2)$. Nun kannst du den Term $x-2$ kürzen zu $f'\left(2\right)=\lim\limits_{x\to 2}(x+2)=4$.
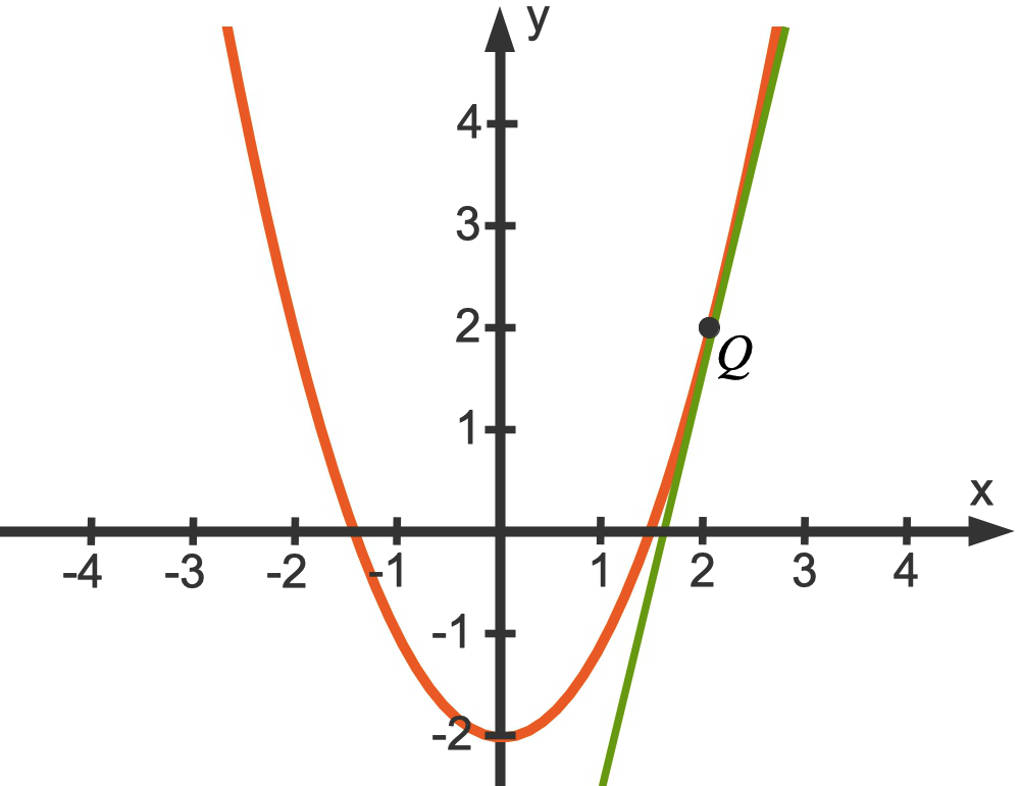
Dies ist die Steigung der Tangente an den Funktionsgraphen von $f$ im Punkt $Q(2|2)$.
h-Methode
Du kannst an Stelle des Grenzwertes $\lim\limits_{x\to x_{0}}$ auch $x=x_{0}+h$ ersetzen. So kommst du zu dem Grenzwert $\lim\limits_{h\to 0}$.
Auch hierfür schauen wir uns das obige Beispiel an:
$f'\left(2\right)=\lim\limits_{h\to 0} \frac{f(2+h)-f(2)}{h}=\lim\limits_{h\to 0}\frac{(2+h)^2-2-(2^2-2)}{h}=\lim\limits_{h\to 0}\frac{4+4h+h^2-4}{h}=\lim\limits_{h\to 0}\frac{h^2+4h}{h} $
Nun kannst du in dem Zählerterm $h$ ausklammern zu $h(h+4)$ und schließlich kürzen. So erhältst du $f'(2)=\lim\limits_{h\to 0}(h+4)=4$.
Natürlich erhältst du den gleichen Grenzwert.
Testeinsetzen
Beim Testeinsetzen wählst du eine Folge von $x$-Werten, welche gegen $x_{0}$ gehen. Zu jedem dieser Werte berechnest du den zugehörigen Funktionswert. Anhand dieser Funktionswerte kannst du den Grenzwert ablesen. Dieses Verfahren ist mathematisch nicht ganz korrekt. Im Zusammenhang mit den Funktionen, welche du in der Schule kennenlernen wirst, führt es jedoch zu dem richtigen Grenzwert.
Alle Videos zum Thema
Videos zum Thema
Ableitung einer Funktion an einer Stelle: f '(xₒ) (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Ableitung einer Funktion an einer Stelle: f '(xₒ) (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Meter
- orthogonal





 Differentialquotient – Anstieg eines Funktionsgraphen in einem Punkt
Differentialquotient – Anstieg eines Funktionsgraphen in einem Punkt
 Steigung in einem Punkt
Steigung in einem Punkt












