Grundlagen zur Wahrscheinlichkeit

Inhaltsverzeichnis zum Thema

• Was ist Wahrscheinlichkeit?
• Zufallsversuche

Was ist Wahrscheinlichkeit?

Die Wahrscheinlichkeitsrechnung ist neben der Statistik ein Teil der Stochastik.

Mit Wahrscheinlichkeiten rechnen wir, wenn es um Zufallsversuche geht. Wenn wir als Zufallsversuch den dreifachen Münzwurf betrachten, gibt es insgesamt acht mögliche Kombinationen mit Kopf $\text{K}$ und Zahl $\text{Z}$. Diese bezeichnen wir als Ergebnismenge. Die möglichen Kombinationen sind im folgenden Baumdiagramm dargestellt:

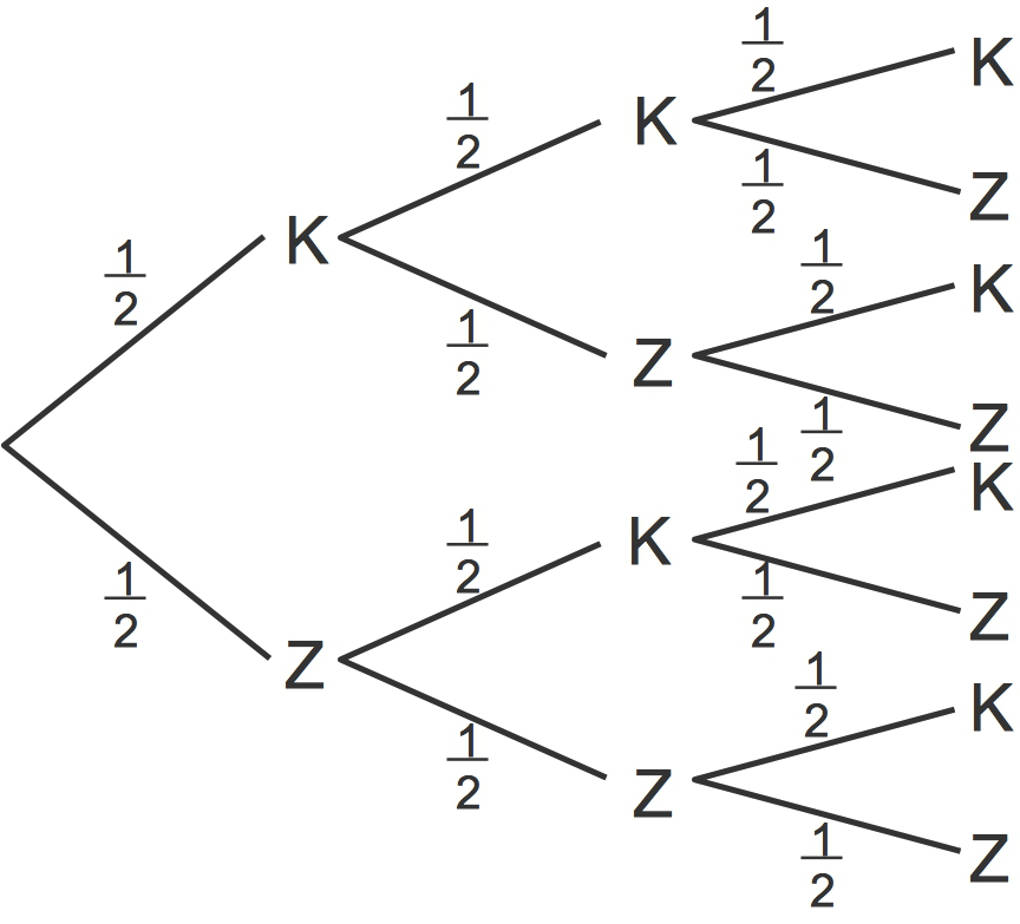
Die Ergebnismenge $(\Omega)$ ist die Menge aller möglichen Ergebnisse eines Zufallsversuchs. Ergebnisse eines Zufallsversuchs sind die Möglichkeiten, für die wir uns interessieren. Geht es darum, zweimal Kopf zu werfen, konzentrieren wir uns auf folgende Ergebnisse:

$(\text{Z;K;K}), (\text{K;K;Z}), (\text{K;Z;K})$

Ein Ereignis $E$ ist eine Teilmenge einer Ergebnismenge. Wenn wir nun die drei obigen Ergebnisse, also das Ereignis genau zweimal Kopf zu werfen als Anteil an allen Möglichkeiten (Ergebnismenge) ausdrücken möchten, können wir dies als Bruch, Dezimalzahl oder Prozent angeben:

$P(E) = \frac{3}{8} = 0,375 = 37,5\%$

Die Wahrscheinlichkeit eines Ereignisses ist der Anteil zutreffender Ergebnisse an der Ergebnismenge. Sie ist eine Zahl zwischen $0$ und $1$, lässt sich als Bruch oder relative Häufigkeit angeben.

Zufallsversuche

Als ersten Zufallsversuch betrachten wir das einmalige Würfeln.

Hierbei handelt es sich um einen Laplace-Versuch, da jedes Ergebnis die gleiche Wahrscheinlichkeit $P$ hat, nämlich:

$P=\frac{1}{\text{Anzahl aller möglichen Ergebnisse}}$

Die Ergebnismenge $\Omega$ besteht aus allen Zahlen auf dem Würfel, also:

$\Omega = \{1;2;3;4;5;6\}$

Das Ereignis $E$ soll das Würfeln einer Primzahl beschreiben. Es enthält somit folgende Ergebnisse:

$E = \{2;3;5\}$

Die Wahrscheinlichkeit $P(E)$ berechnen wir als Anteil des Ereignisses $E$ an der Ergebnismenge $\Omega$, also:

$P(E) =\frac{3}{6} = \frac{1}{2} = 0,5$

Einen zweiten Laplace-Versuch stellt das Ziehen von Losen dar.

Geht man von insgesamt $100$ Losen in der Lostrommel aus, unter denen sich $5$ Gewinnlose befinden, so ermitteln wir die Wahrscheinlichkeit für das Ziehen eines Gewinnloses, indem wir den Anteil der Gewinnlose an allen Losen wie folgt berechnen:

$\frac{5}{100} = \frac{1}{20} = 0,05$

Beim dritten Zufallsversuch geht es um das Ziehen von Kugeln aus einer Urne.

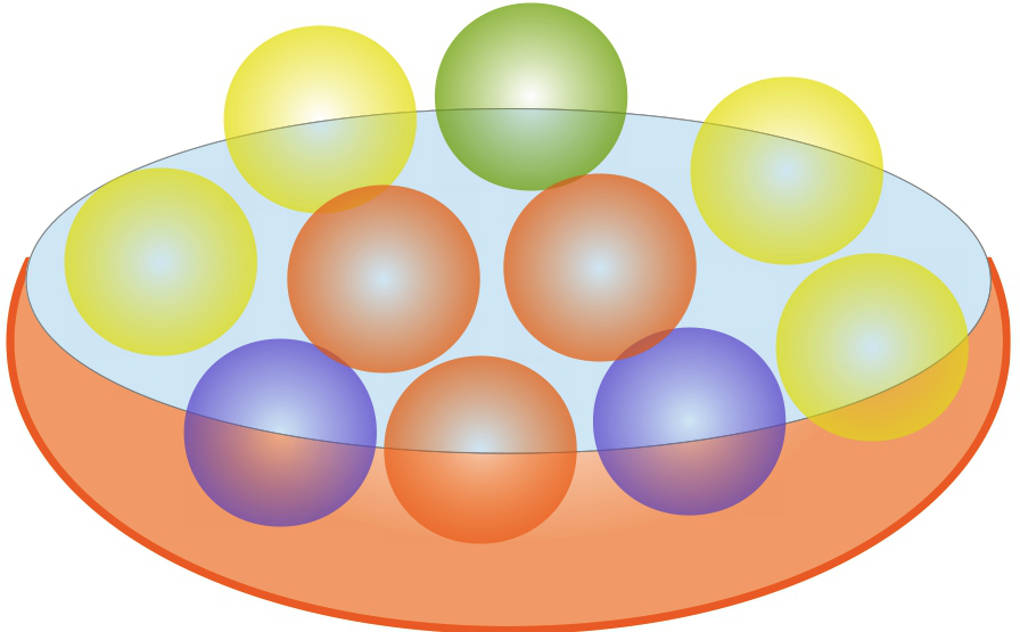
In der Urne befinden sich insgesamt $10$ nummerierte Kugeln, davon sind $4$ gelb, $3$ rot, $2$ blau und $1$ grün. Je nachdem, ob wir uns nun für die Nummerierung von $1$ bis $10$ oder die vier verschiedenen Farben der Kugeln interessieren, erhalten wir unterschiedliche Ergebnismengen.

Möglichkeit 1: Betrachtung der $10$ nummerierten Kugeln

In diesem Fall können wir die Ergebnismenge wie folgt angeben:

$\Omega = \{1;2;3;4;5;6;7;8;9;10\}$

Für die Wahrscheinlichkeiten der möglichen Ergebnisse aus der Ergebnismenge $\Omega$ gilt:

$P(1) = P(2) = P(3) = … = P(10) = \frac{1}{10}$

Somit handelt es sich hierbei wieder um einen Laplace-Versuch, denn jede Kugel hat mit $\frac{1}{10}$ die gleiche Wahrscheinlichkeit.

Möglichkeit 2: Betrachtung der vier verschiedenen Farben

Wenn wir die vier unterschiedlichen Farben betrachten, erhalten wir folgende Ergebnismenge:

$\Omega =\{\text{gelb;rot;blau;gr}\ddot{\text{u}}\text{n}\}$

Für die Wahrscheinlichkeiten der Ergebnisse aus der Ergebnismenge gilt nun:

$\begin{array}{lllll} P(\text{gelb}) &=& \frac{4}{10} &=& 0,4 \\ P(\text{rot}) &=& \frac{3}{10} &=& 0,3 \\ P(\text{blau}) &=& \frac{2}{10} &=& 0,2 \\ P(\text{gr}\ddot{\text{u}}\text{n}) &=& \frac{1}{10} &=& 0,1 \end{array}$

Zudem gilt:

$P(\text{gelb}) + P(\text{rot}) + P(\text{blau}) + P(\text{gr}\ddot{\text{u}}\text{n}) = 1$

Ordnet man allen Elementen einer Menge Zahlen zwischen $0$ und $1$ zu, sodass deren Summe $1$ ist, sind diese Zahlen Wahrscheinlichkeiten.

Nun können wir uns dafür interessieren, wie groß die Wahrscheinlichkeit ist, eine rote oder grüne Kugel zu ziehen. Wir definieren zunächst das Ereignis $E$ wie folgt:

$E: \{\text{rot; gr}\ddot{\text{u}}\text{n}\}$

Für die Wahrscheinlichkeit des Ereignisses $E$ betrachten wir die einzelnen Wahrscheinlichkeiten für rot und grün und zählen diese zusammen:

$P(E)= P(\text{rot})+P(\text{gr}\ddot{\text{u}}\text{n}) = \frac{3}{10} + \frac{1}{10} = \frac{4}{10} = 0,4$

Die Wahrscheinlichkeit eines Ereignisses ist die Summe der Wahrscheinlichkeiten, die zum Ereignis gehören.