Flächeninhalt und Umfang von Rechtecken
Ein Rechteck hat einen Umfang und einen Flächeninhalt. Wie werden diese berechnet? In welchem Zusammenhang kommen solche Aufgaben vor?
Beliebteste Videos
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist ein Rechteck?
- Der Umfang eines Rechtecks
- Der Flächeninhalt eines Rechtecks
- Zusammengesetzte Figuren
Was ist ein Rechteck?
Ein Rechteck ist eine ebene Figur. Es hat vier Ecken, ist also ein Viereck, und hat auch vier Seiten und vier Winkel. Das Besondere an einem Rechteck ist, wie du an dem Namen merkst, dass alle vier Winkel rechte Winkel sind. Die einander gegenüberliegenden Seiten sind parallel und gleich lang:
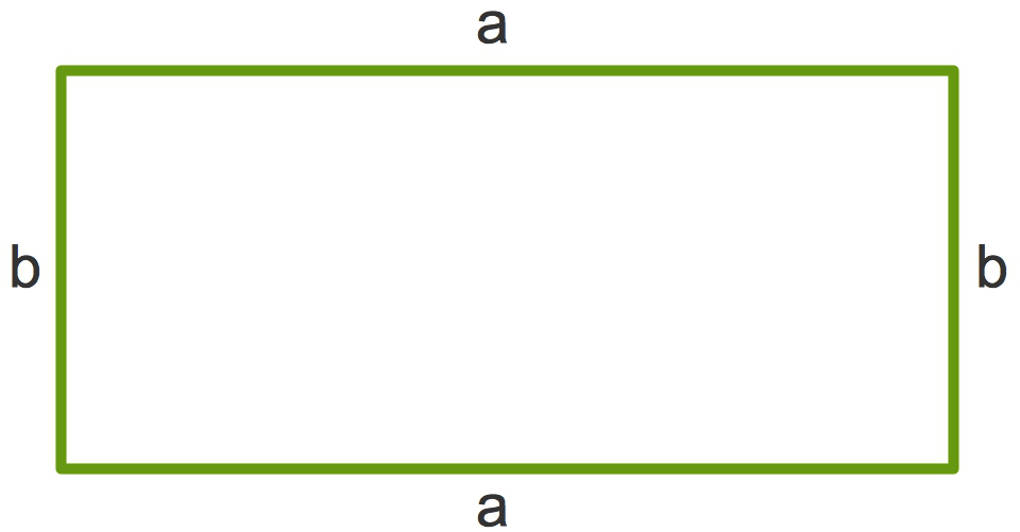
Übrigens, auch ein Quadrat ist ein Rechteck. Bei einem Quadrat sind alle Seiten gleich lang.
Der Umfang eines Rechtecks
Wie berechne ich den Umfang eines Rechtecks? Für die Berechnung des Umfangs u eines Rechtecks addierst du die Längen der vier Seiten:
$u=a+b+a+b=2a+2b=2(a+b)$.
Ein Sonderfall des Rechtecks ist das Quadrat. Bei diesem besonderen Rechteck sind alle Seiten gleich lang. Du kannst den Umfang dann so berechnen: $u=a+a+a+a=4a$.
Beispiel „Laufstrecke“
Paul möchte an einem Laufwettbewerb teilnehmen. Der Verlauf der Strecke entspricht der Form eines Rechtecks. Die Seitenlängen sind $a=300~m$ und $b=400~m$. Wie lang ist die gesamte Laufstrecke?
- Paul addiert die beiden Seitenlängen: $a+b=300~m+400~m=700~m$.
- Nun multipliziert er das Ergebnis mit $2$ und erhält: $2\cdot 700~m=1400~m$.
Die Laufstrecke ist also $1400~m$ lang.
Beispiel „Schwimmbecken“
Familie Losch möchte an die beiden längeren Seiten ihres rechteckigen Schwimmbeckens einen Zaun bauen. Das Schwimmbecken hat einen Umfang von $u=40~m$. Die kürzere Seitenlänge beträgt $5~m$. Wie viele Meter Zaum braucht Familie Losch für beide Zaunabschnitte?
- Dieses Mal ist der Umfang sowie die Seitenlänge der beiden kürzeren, sich gegenüberliegenden Seiten bekannt.
- Gesucht ist die Länge beider längerer Seiten des Dreiecks. Da beide Seiten gleich lang sind, kannst du die Seitenlänge jeweils mit einer Variable, zum Beispiel $a$, beschreiben.
Nun kannst du die Formel für den Umfang verwenden, $u=2a+2b$, und die bekannten Größen $u=40~m$ sowie $b=5~m$ einsetzen:
- $40~m=2a+2\cdot 5~m$
- Ziehe jetzt auf beiden Seiten der Gleichung $2\cdot 5~m=10~m$ ab. Du erhältst $30~m=2a$.
- Teile noch durch $2$. Das führt zu $15~m=a$.
Somit ist die längere Seite $15~m$ lang. Der Zaun soll auf beiden Seiten gebaut werden. Das heißt, es werden $2\cdot 15~m=30~m$ Zaun benötigt.
Der Flächeninhalt eines Rechtecks
Den Flächeninhalt eines Rechtecks kannst du wie folgt berechnen:
$A=a\cdot b$.
Du kannst dir merken: Länge mal Breite gleich Flächeninhalt.
Da bei einem Quadrat die Seiten gleich lang sind, ist der Flächeninhalt eines Quadrates $A=a\cdot a=a^2$.
Beispiel „Schwimmbecken“
Das Schwimmbecken von Familie Losch soll einen neuen Boden bekommen. Um auszurechnen, wie viel das kostet, muss der Flächeninhalt des Bodens berechnet werden.
- Da das Schwimmbecken rechteckig ist, mit den Seitenlängen $a=15~m$ und $b=5~m$, kannst du die Flächenformel $A=a\cdot b$ verwenden.
- Du setzt nun die bekannten Größen ein: $A=(15~m)\cdot (5~m)=75~m^2$.
Der Boden hat den Flächeninhalt $A=75~m^2$.
Beispiel „Hamsterhaus“
Paul möchte für seinen Hamster ein Haus bauen. Er hat gelesen, dass ein Hamster mindestens eine Fläche von $4000~cm^2$ benötigt. Paul entscheidet sich für ein klassischen Haus mit rechteckigem Boden. Die eine Seite des Bodens des Hauses ist durch den geplanten Standort mit $50~cm$ vorgegeben. Wie lang muss die beiden Seite mindestens sein, damit der Hamster genügend Platz hat?
Paul überlegt: Da der Boden die Form eines Rechtecks haben soll, genügt es, die Länge einer der beiden anliegenden Seiten $b$ zu berechnen. Paul rechnet mit der Flächenformel $A=a \cdot b$ und setzt für den Flächeninhalt $ A=4000~cm^2 $ und $a$ die Seitenlänge $50~cm$ ein .
- Er stellt die folgende Formel auf: $4000~cm^2=(50~cm)\cdot b$.
- Nun teilt er durch $50~cm$, um die Gleichung nach $b$ umzustellen und erhält:
$ \quad b= \frac{4000~cm^2}{50~cm}$.
- Er kann $cm$ und $50$ kürzen. Damit kommt er zu der Länge der Seite
$ \quad b= \frac{4000~cm^2}{50~cm}=80~cm$.
- Dann ist $b= 80~cm$ die gesuchte Mindestlänge.
Paul muss also die unbekannte Seitenlänge mindesten $80~cm$ lang machen.
Zusammengesetzte Figuren
Es gibt Figuren, deren Flächeninhalt man aus Rechtecken zusammensetzen kann. Zuletzt schauen wir uns noch Beispiele von Figuren an, die aus mehreren Rechtecken und (oder) Quadraten zusammengesetzt sind.
Beispiel zum Flächeninhalt
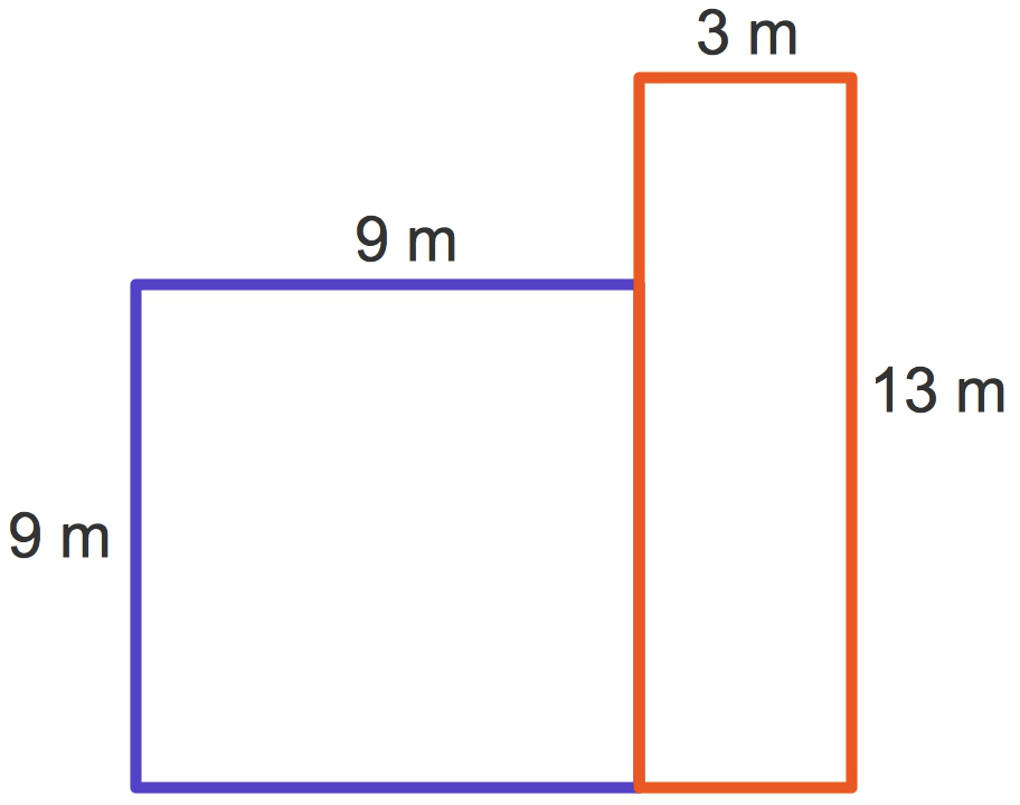
Hier siehst du ein blaues Quadrat und ein rotes Rechteck. Wenn du den Flächeninhalt der gesamten Figur berechnen möchtest, berechnest du den Flächeninhalt dieser beiden Figuren und addierst diese:
- Quadrat: $A_1=(9~m)\cdot(9~m)=81~m^2$
- Rechteck: $A_2=(3~m)\cdot(13~m)=39~m^2$
Damit ist der gesamte Flächeninhalt: $A=A_1+A_2=81~m^2+39~m^2=120~m^2$.
Beispiel zum Umfang
Du kannst auch den Umfang dieser zusammengesetzten Figur berechnen. Dafür stellst du dir vor, dass du, zum Beispiel an der Ecke unten links startest und zuerst nach oben gehst und dann immer weiter, bis du wieder am Start angekommen bist. In der Grafik ist dieser "Weg" grün gekennzeichnet. Beachte, dass du im Fall des Umfangs nicht den Umfang der beiden Figuren addieren kannst. Die Strecke, an denen die beiden Figuren zusammengesetzt sind, darf nicht mit eingerechnet werden:
$u=9~m+9~m+(13~m-9~m)+3~m+13~m+3~m+9~m=50~m$.
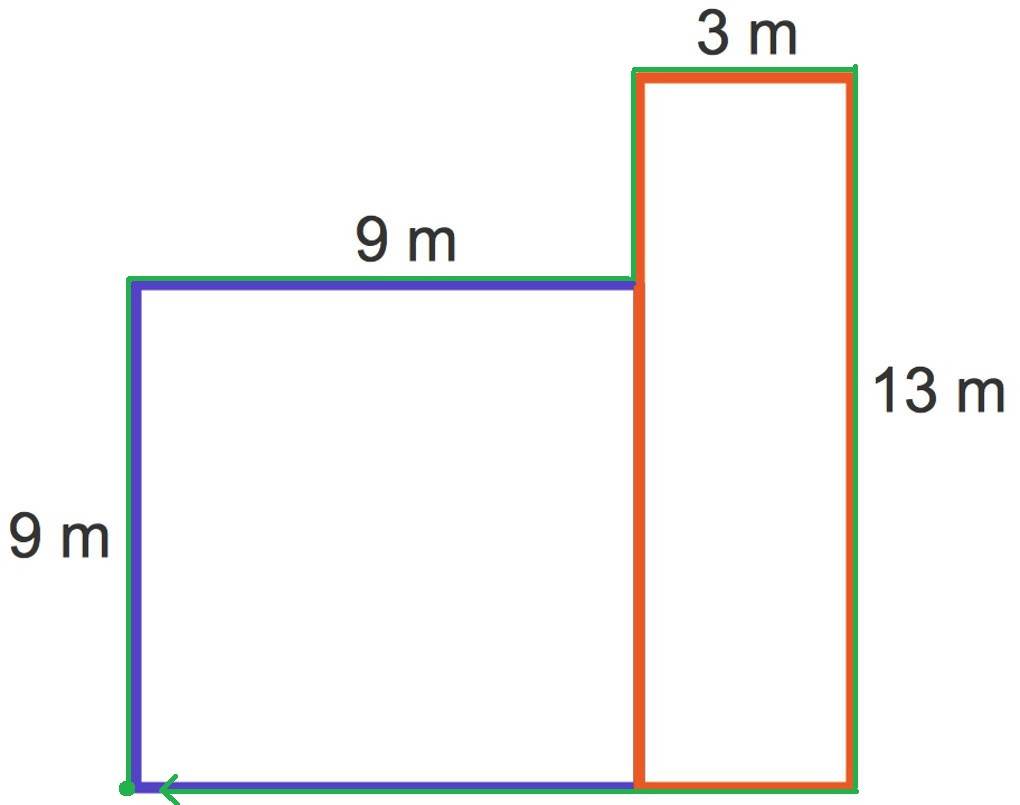
Nun kannst du dich natürlich fragen, wo solche zusammengesetzten Figuren vorkommen. Das könnte der Grundriss eines Raumes sein.
- Den Flächeninhalt berechnest du, wenn du einen neuen Boden in dem Raum haben möchtest.
- Den Umfang berechnest du, wenn du neue Fußbodenleisten anbringen willst.
Alle Videos zum Thema
Videos zum Thema
Flächeninhalt und Umfang von Rechtecken (8 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Flächeninhalt und Umfang von Rechtecken (8 Arbeitsblätter)
-
 Flächeninhalt und Umfang von Quadraten
PDF anzeigen
Flächeninhalt und Umfang von Quadraten
PDF anzeigen -
 Fläche und Umfang eines Rechtecks
PDF anzeigen
Fläche und Umfang eines Rechtecks
PDF anzeigen -
 Flächeninhalt von Rechtecken
PDF anzeigen
Flächeninhalt von Rechtecken
PDF anzeigen -
 Umfang von Rechtecken
PDF anzeigen
Umfang von Rechtecken
PDF anzeigen -
 Umfang eines Rechtecks – Übung
PDF anzeigen
Umfang eines Rechtecks – Übung
PDF anzeigen -
 Flächeninhalt von aus Rechtecken zusammengesetzten Figuren
PDF anzeigen
Flächeninhalt von aus Rechtecken zusammengesetzten Figuren
PDF anzeigen -
 Flächeninhalt von zusammengesetzten Flächen
PDF anzeigen
Flächeninhalt von zusammengesetzten Flächen
PDF anzeigen -
 Flächeninhalt von zusammengesetzten Rechtecken
PDF anzeigen
Flächeninhalt von zusammengesetzten Rechtecken
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Brüche multiplizieren – Übungen
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen























