Graphisches Ableiten – Übung (1)

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Graphisches Ableiten – Übung (1)
In diesem Video wirst du sehen, wie man die Funktionen f(x) = x² und f(x) = x³ graphisch ableitet. Die einzelnen Schritte werden dir dabei genaustens erklärt.
Transkript Graphisches Ableiten – Übung (1)
Hallo! Heute üben wir, wie man anhand des Graphens einer Potenzfunktion den Graphen der Ableitungsfunktion bestimmt.
Regeln beim Ableiten
Beim Ableiten musst du dir allgemein folgendes merken:
- An den Extremstellen der Ursprungsfunktion f(x) ist die Steigung gleich null. Daher hat die Ableitungsfunktion f'(x) hier Nullstellen.
- An den Wendestellen der Ursprungsfunktion f(x) ist die Steigung maximal bzw. minimal. Daher hat die Ableitungsfunktion f'(x) hier Extremstellen.
- Eine positive Steigung an einer Stelle der Ursprungsfunktion führt bei der Ableitungsfunktion zu einem positiven y-Wert an dieser Stelle.
- Eine negative Steigung an einer Stelle der Ursprungsfunktion führt bei der Ableitungsfunktion zu einem negativen y-Wert an dieser Stelle.
- Die Steigung der Ursprungsfunktion an der Stelle x1, ist der Funktionswert der Ableitungsfunktion an dieser Stelle x1.
Graph bestimmen: Beispiel f(x) = x²
Als Beispiele schauen wir uns die Funktionen f(x) = x² und g(x) = x³ an. Betrachten wir zunächst die Funktion f(x) = x². Wenn wir eine Wertetabelle für diese Funktion erstellen, erhalten wir für x–Werte von -3 bis +3 folgende Ergebnisse:
Für den x- Wert -3 erhalten wir den Funktionswert 9, für x gleich -2 erhalten wir den y- Wert gleich 4, für x gleich -1 erhalten wir den y- Wert 1 und für x gleich null erhalten wir den Funktionswert 0. Die restlichen Punkte ergeben sich aus der Achsensymmetrie des Funktionsgraphens zur y- Achse.
Der Funktionsgraph sieht folgendermaßen aus.
Nun suchen wir mögliche Extremstellen, also Stellen, an denen die Steigung Null ist und an die wir eine waagerechte Tangente anlegen können. Das ist nur an der Stelle x = 0 der Fall.
Aus dem Merksatz 5: Die Steigung der Ursprungsfunktion an der Stelle x1, ist der Funktionswert der Ableitungsfunktion an dieser Stelle x1. Somit geht der Graph der Ableitungsfunktion also durch den Punkt P1(0|0).
Jetzt suchen wir mögliche Wendestellen. Die Wendestellen finden sich immer dort, wo der Graph von einer Linkskurve in eine Rechtskurve übergeht oder eben umgekehrt von rechts nach links. In dieser Funktion aber haben wir durchgängig eine Linkskurve. Da es keinen Übergang zu einer Rechtskurve gibt, haben wir deshalb auch keine Wendestelle.
Nun sehen wir uns an, in welchen Abschnitten die Steigung der Funktion positiv und in welchen negativ ist. Links vom Ursprung haben wir eine negative Steigung und rechts eine positive Steigung.
Wir wissen, dass eine positive Steigung an einer Stelle der Ursprungsfunktion bei der Ableitungsfunktion zu einem positiven y-Wert an dieser Stelle führt.
Hingegen eine negative Steigung an einer Stelle der Ursprungsfunktion, bei der Ableitungsfunktion zu einem negativen y-Wert an dieser Stelle führt.
Der Graph der Ableitungsfunktion verläuft somit im ersten und im dritten Quadraten unseres Koordinatensystem. Versuchen wir jetzt noch herauszufinden, wo die Steigung 1, 2, 3 oder vielleicht sogar 4 ist. Nach dem Merksatz 5 hilft uns dies, um die Lage einiger Punkte des Graphens der Ableitungsfunktion zu erhalten .
Wenn wir eine Stelle mit der Steigung 1 suchen, dann suchen wir eine Stelle, an der die angelegte Tangente die Steigung 1 besitzt. Man also immer eine Einheit nach rechts und eine Einheit nach oben geht. Also etwa an der Stelle x = 0,5. Ein weiterer Punkt des Graphens der Ableitungsfunktion ist somit P2 (0,5|1).
Jetzt versuchen wir eine Tangente anzulegen, die die doppelte Steigung hat. Das müsste etwa an der Stelle x = 1 sein. Wir erhalten den Punkt P3 (1|2) des Graphens der Ableitungsfunktion. Die Steigung 3 finden wir bei etwa x = 1,5. Ein Punkt der Ableitungsfunktion ist somit P4 (1,5|3).
Die Steigung +4 schaffen wir auch noch, allerdings ist sie schon ein bisschen steil und daher nicht mehr so gut zu bestimmen. Der dazugehörige x-Wert liegt bei 2, also etwa hier. Wir erhalten somit den weiteren Punkt P5(2|4) für den Graphen der Ableitungsfunktion.
Wenn wir auf der linken Seite der Parabel die Steigungen -1, -2, -3 und -4 ermitteln, erkennen wir, dass diese die gleichen Beträge, wie auf der rechten Seite haben, nur mit negativem Vorzeichen.
Wir erhalten somit folgende Wertetabelle für den Graphen der Ableitungsfunktion.
Wenn wir jetzt in unserem neuen Koordinatensystem alle Punkte einzeichnen und miteinander verbinden, dann erhalten wir eine Gerade. Hier können wir sogar recht einfach die Funktionsgleichung der Ableitung ablesen. Es handelt sich um f(x) = 2x.
So, das war jetzt eine mögliche Herangehensweise bei der Funktion f(x) = x².
Graph bestimmen: Beispiel g(x) = x³
In unserem zweiten Beispiel g(x) = x³ sieht die Wertetabelle so aus. Aus der Wertetabelle lesen wir dir Punkte (-3|-27), (-2|-8), (-1|-1), (0|0), (1|1), (2|8) und (3|27) ab. Der Graph der Funktion sieht folgendermaßen auß. Er ist punktsymmetrisch zum Koordinatenursprung.
Zuerst sehen wir wieder nach, ob wir eine Stelle finden, an der die Steigung der Tangenten Null ist, also die angelegte Tangente waagerecht liegt. Das ist bei x = 0 der Fall. Hier haben wir einen Sattelpunkt. Der Graph der Ableitungsfunktion geht folglich durch den Koordinatenursprung.
Wenn wir nach der Krümmung schauen, sehen wir, dass der Graph der Funktion links neben dem Wendepunkt eine Rechtskurve und rechts neben dem Wendepunkt eine Linkskurve beschreibt. Dazwischen, also bei x = 0, liegt die Wendestelle, die Übergangsstelle zwischen Linkskurve und Rechtskurve.
Wenn wir untersuchen, wo wir eine positive bzw. negative Steigung haben, dann stellen wir hier fest, dass bis auf unsere Sattelstelle alle Steigungen positiv sind. Aus Merksatz 3 folgt, dass die y- Koordinaten der Punkte der Ableitungsfunktion alle positiv sind. Der Graph der Ableitungsfunktion kann somit nur im ersten und zweiten Quadraten unseres Koordinatensystems verlaufen.
Jetzt versuchen wir wieder markante Steigungen wie 1, 2, 3 zu finden; negative haben wir ja nicht. Diesmal kommen alle Steigungen doppelt vor. Die Steigung 1 gibt es etwas rechts von x = +0,5 und einmal etwas links von x= -0,5. Die Steigung 2 finden wir ungefähr bei x = +0,8 und -0,8. Und die Steigung 3 bei x=1 und x=-1. Danach werden die Werte schnell sehr groß.
Wie sieht nun unsere Wertetabelle für den Graphen der Ableitungsfunktion aus? Wir erhalten folgende Wertetabelle für den Graphen der Ableitungsfunktion.
Eingezeichnet sieht das dann wie eine in y- Richtung gestreckte Parabel aus. Dieser Graph stellt jetzt ungefähr die jeweilige momentane Steigung der Ursprungfunktion g von x gleich x hoch drei dar. Der von uns skizzierte Graph ähnelt dem Graphen der Funktion mit der Funktionsgleichung f(x)=3x². Genau genommen wird die Ableitungsfunktion g'(x) durch 3 x² beschrieben.
Zusammenfassung
Wir fassen zusammen: Du siehst, es ist gar nicht so schwer, eine Funktion graphisch abzuleiten. Such Dir alle markanten Stellen und Abschnitte des Graphen der Funktion heraus und entwickle daraus Schritt für Schritt die Wertetabelle und dann den Graphen Deiner Ableitungsfunktion.
Graphisches Ableiten – Übung (1) Übung
-
Erstelle eine Wertetabelle für $f(x)=x^2$.
TippsDie Funktion ist oben gegeben. Du musst die $x$-Werte in die Funktionsgleichung einsetzen.
Das ist der Graph von $f$ in einem Koordinatensystem.
Die Wertetabelle gibt die Koordinaten verschiedenster Punkte des Graphen an.
LösungWenn du Werte für eine Wertetabelle berechnest, musst du die $x$-Werte, zu denen du Funktionswerte ($y$-Werte) berechnen möchtest, in die Funktionsgleichung einsetzen.
Dabei musst du besonders bei Potenzfunktionen auf die Vorzeichen achten.
Die Werte für die Wertetabelle ergeben sich so:
$f(x)=x^2$
$f(-3)=(-3)^2=9$
$f(-2)=(-2)^2=4$
$f(-1)=(-1)^2=1$
$f(0)=(0)^2=0$
$f(1)=(1)^2=1$
$f(2)=(2)^2=4$
$f(3)=(3)^2=9$
Und somit erhältst du eine vollständige Wertetabelle (Bild).
-
Bestimme den Ableitungsgraphen von $g$.
TippsEine Wertetabelle für $g$ sieht so aus:
$\begin{array}{c|c|c|c|c|c|c|c} x&-3&-2&-1&0&1&2&3 \\ \hline y&-27&-8&-1&0&1&8&27 \end{array}$
So sieht der Graph von $g$ aus. Du kannst ihn auf ein Blatt übertragen, um dort die Steigung von $g$ an verschiedenen Stellen abzulesen.
Die Steigung von $g$ an der Stelle...
- $0$ beträgt $0$
- $-1$ beträgt $3$
- $1$ beträgt $3$
Die Steigung einer Funktion an einer bestimmten Stelle entspricht dem $y$-Wert der Ableitungsfunktion an dieser Stelle.
LösungZunächst musst du dir eine Wertetabelle für die Funktion $g(x)$ erstellen. Diese könnte dann so aussehen:
$\begin{array}{c|c|c|c|c|c|c|c} x&-3&-2&-1&0&1&2&3 \\ \hline y&-27&-8&-1&0&1&8&27 \end{array}$
Mit ihr kannst du dann die Funktion zeichnen. Wenn du den Funktionsgraphen $g$ betrachtest, siehst du, dass sie bis auf eine Stelle monoton steigt, das heißt, unser Ableitungsgraph muss im positiven Wertebereich verlaufen und die $x$-Achse am Ursprung berühren, da unser Graph hier die Steigung $0$ besitzt.
Das trifft nur auf die erste, dritte und fünfte Parabel zu. Sehen wir uns nun die Steigungen an.
Unser Ausgangsgraph besitzt bereits an der Stelle $1$ eine Steigung von $3$.
Das bedeutet, unser Ableitungsgraph $g'$muss den Punkt $(1|3)$ besitzen. Das ist nur bei dem ersten Bild, der in $y$-Richtung gestauchten Parabel der Fall. Sie muss unser Ableitungsgraph zu $g$ sein. Die Funktionsgleichung der Ableitungsfunktion lautet $g'(x)=3\cdot x^2$.
-
Ergänze die Wertetabelle zu $f(x)=-x^2$.
TippsDie Funktionsgleichung ist oben gegeben. Du musst die $x$-Werte oder die Funktionswerte in die Funktionsgleichung einsetzen.
Vor dem $x^2$ steht ein Minus. Die Parabel ist also nach unten geöffnet.
$-x^2$ und $(-x)^2$ sind zwei verschiedene Ausdrücke mit verschiedenen Ergebnissen.
LösungBetrachten wir die Funktionsgleichung: $f(x)=-x^2$
Das Minus steht vor $x^2$ ist nicht durch eine Klammer an den Exponenten gebunden. Das bedeutet, dass alle Ergebnisse nach dem Quadrieren noch ein Minus erhalten.
Nur bei $(-x)^2$ würde das Minus direkt in die Rechnung eingehen und man würde nur positive Ergebnisse erhalten. In diesem Fall kann es aber nur negative Funktionswerte geben.
Die Wertetabelle (Bild) ergibt sich so:
$f(-3)=-(-3)^2=-9$
$f(-2)=-(-2)^2=-4$
$f(x)=-1 \Leftrightarrow -x^2 = -1 \Leftrightarrow x=\pm 1$
Wir setzen $x=-1$ ein, da wir uns auf der linken Seite der Wertetabelle, also im negativen Wertebereich für $x$, befinden. Außerdem gibt es $x=+1$ bereits weiter rechts in der Wertetabelle.
$f(0)=-(0)^2=0$
$f(1)=-(1)^2=-1$
$f(x)=-9 \Leftrightarrow -x^2=-9 \Leftrightarrow x=\pm 3$
Wir setzen $x=3$ ein, da wir uns auf der rechten Seite der Wertetabelle, also im positiven Wertebereich für $x$, befinden. Außerdem gibt es $x=-3$ bereits ganz links in der Wertetabelle.
$f(x)=-16 \Leftrightarrow -x^2=-16 \Leftrightarrow x=\pm 4$
Wir setzen $x=4$ ein, da wir uns auf der rechten Seite der Wertetabelle, also im positiven Wertebereich für $x$, befinden.
-
Ermittle zu jeder Funktion ihren Ableitungsgraphen.
TippsAn den Extremstellen von $f'$ kannst du die Wendestellen von $f$ erkennen.
An den Nullstellen von $f'$ kannst du die Extremstellen von $f$ erkennen.
Wertetabellen und Skizzen zu den einzelnen, möglichen Funktionen können sehr hilfreich sein.
Der Funktionswert des Ableitungsgraphen an einer Stelle gibt die Steigung der Ausgangsfunktion an dieser Stelle an.
LösungDer dritte Graph ist eine Parallele zur x-Achse, die durch $y=3$ verläuft. Da uns die Funktionswerte der Ableitungsgraphen immer die Steigung der Ausgangsfunktion angeben, muss unsere gesuchte Funktion permanent die Steigung $m=3$ besitzen. Das kann nur bei einer linearen Funktion der Fall sein. Die allgemeine Funktionsgleichung einer linearen Funktion lautet $f(x)=m\cdot x+n$. Da wir die Steigung mit $m=3$ als Parameter vor dem $x$ ablesen können, ist unsere gesuchte Funktionsgleichung $f(x)=3x$.
Wir schauen uns den ersten Graphen an. Dieser Graph verläuft vollständig im positiven Bereich und gibt somit an, dass der Graph der Ausgangsfunktion stetig steigt - bis auf die Stelle $x=0$, dort muss die Steigung null sein. Es handelt sich hierbei um eine quadratische Funktion durch den Ursprung. Bei der Ableitung wird der Grad der Funktion um $1$ vermindert, also kommt für die Ausgangsfunktion nur eine kubische Funktion mit dem Grad $3$ in frage. Wir erhalten also die Funktionsgleichung $f(x)=x^3$.
Wir schauen uns den zweiten Graphen an. Es ist eine lineare Funktion, die zuerst im negativen Bereich verläuft, dann im Ursprung die $x$-Achse schneidet und dann im positiven Bereich verläuft. Also suchen wir eine Funktion als Ausgangsfunktion, deren Graph erst fällt, im Ursprung eine Extremstelle besitzt und danach wieder steigt. Die Extremstelle ist also ein Tiefpunkt. Ein solches Aussehen kennen wir nur von einer nach oben geöffneten Parabel. Und die einzige, nach oben geöffnete Parabel, wird durch $f(x)=x^2$ beschrieben.
Wir schauen uns den vierten Graphen an. Gesucht ist ein Graph, der zuerst positiv steigt, im Ursprung eine Extremstelle besitzt und danach negativ steigt bzw. fällt - also eine nach unten geöffnete Parabel. Dieses Bild passt nur auf die Funktion $f(x)=-3x^2$, da die Steigung sehr groß ist.
-
Beschreibe den Zusammenhang zwischen einer Funktion und seiner Ableitungsfunktion.
TippsSteigungen an bestimmten Stellen der Ausgangsfunktion geben immer Auskunft über den Funktionswert der Ableitungsfunktion an dieser Stelle.
An Extremstellen ist die Steigung null, an Wendestellen maximal bzw. minimal.
LösungWichtige Merksätze, die du dir aufschreiben solltest, lauten:
- An Extremstellen von $f$ besitzt $f'$ seine Nullstellen, da dort die Steigung von $f$ null ist.
- An Wendestellen von $f$ besitzt $f'$ seine Extremstellen, da dort die Steigung von $f$ minimal bzw. maximal ist.
- Ist die Steigung von $f$ an einer Stelle $a$ positiv, so besitzt $f'$ an dieser Stelle $a$ einen positiven Funktionswert. Es gilt $f'(a)>0$.
- Ist die Steigung von $f$ an einer Stelle $a$ negativ, so besitzt $f'$ an dieser Stelle $a$ einen negativen Funktionswert. Es gilt $f'(a)<0$.
- Allgemein gilt, dass die Steigung von $f$ an einer Stelle $a$ den Funktionswert von $f'$ an dieser Stelle $a$ angibt, also $f'(a)$.
-
Bestimme den Ableitungsgraphen von $f$.
TippsSo sieht ein Teil der Wertetabelle zu $f$ aus:
$\begin{array}{c|c|c|c|c} x&-2&-1&0&1 \\ \hline y&-7&2&1&2 \end{array}$
Das hier ist der Graph zu $f(x)$.
Die Steigung von $f$ an jeder beliebigen Stelle $a$ gibt den Funktionswert von $f'$ an dieser Stelle $a$ an.
LösungZuerst brauchen wir eine Wertetabelle zu $f$ um den Graphen zeichnen zu können. Darin besteht ein Großteil der Schwierigkeit dieser Aufgabe. Eine Wertetabelle könnte so aussehen: $\begin{array}{c|c|c|c|c|c|c|c} x&-3&-2&-1&0&1&2&3 \\ \hline y&&-7&2&1&2&& \end{array}$
Weitere Funktionswerte ergeben sich so:
$f(2)=-(2)^4 + 2\cdot (2)^2 + 1 = -16 + 8 + 1 = -7$
$f(-3)=-(-3)^4 + 2\cdot (-3)^2 + 1 = -81 + 18 + 1 = -62$
$f(3)=-(3)^4 + 2\cdot (3)^2 + 1 = -81 + 18 + 1 = -62$
Wie du siehst, verschwinden dank der positiven Exponenten zwar die negativen Vorzeichen, doch durch das Minus vor dem ersten Summanden wird dieser immer negativ. Da er den größten Exponenten besitzt, wird somit das Ergebnis auch immer stärker negativ.
Nun kannst du versuchen, die Kurve zu zeichnen (Bild).
Wir sehen zwischen $x_1=-1$ und $x_2=1$ drei Extremstellen der Ausgangsfunktion. Das bedeutet, dort muss unser Ableitungsgraph drei Nullstellen besitzen. Das trifft nur auf den zweiten und letzten Graphen oben zu.
Bei $x_1=-0,5$ und $x_2=0,5$ besitzt $f$ Wendestellen, dort muss unser gesuchter Ableitungsgraph Extremstellen besitzen. Was wir auch in Bild zwei und fünf sehen, nämlich den Tief- und den Hochpunkt.
Der letzte Hinweis ist die Art der Extrempunkte oder die Steigung der Ausgangsfunktion. Wie du in dem Bild sehen kannst, ist die Steigung von links ($-\infty$) bis zum ersten Extrempunkt positiv, also muss die Ableitungsfunktion oberhalb der $x-Achse$ verlaufen. Das trifft eben nur auf den zweiten Funktionsgraphen zu. Die Funktionsgleichung der Ableitungsfunktion lautet $f'(x)=-4 x^3+4 x$.
9'040
sofaheld-Level
6'601
vorgefertigte
Vokabeln
7'588
Lernvideos
35'759
Übungen
32'517
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Winkelsummen in Dreiecken und Vierecken – Übungen
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Brüche multiplizieren – Übungen
- Potenzgesetze




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?



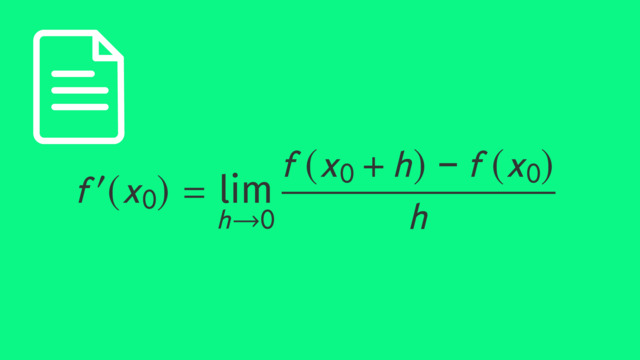










Ich habe nicht verstanden was ist die Unterschied zwischen Ableitung und Ableitungsfunktion.
Hallo R Mollaoglu,
bitte beschreibe genauer, was du nicht verstanden hast. Gib beispielsweise die konkrete Stelle im Video mit Minuten und Sekunden an. Gerne kannst du dich auch an den Fach-Chat wenden, der von Montag bis Freitag zwischen 17-19 Uhr für dich da ist.
Ich hoffe, dass wir dir weiterhelfen können.
Liebe Grüße aus der Redaktion
man versteht null