Proportionale Funktionen: f(x) = m·x

Inhaltsverzeichnis zum Thema

• Was ist eine proportionale Funktion?
• Darstellungen proportionaler Funktionen
• Steigung $m$
• Quotientengleichheit

Was ist eine proportionale Funktion?

Über eine proportionale Zuordnung kommen wir zu einer proportionalen Funktion. Wir betrachten dazu folgendes Beispiel:

Ein Auto legt bei gleichbleibender Geschwindigkeit in zwei Stunden eine Strecke von $100\ \text{km}$ zurück. Wie viel Kilometer ist es in fünf Stunden gefahren?

Um aus den gegebenen Werten den Zielwert zu bestimmen, wählen wir einen Zwischenschritt und erhalten durch Anwendung des Dreisatzes:

Die gesuchte Strecke nach fünf Stunden lässt sich berechnen, indem wir die Strecke für eine Stunde mit $5$ multiplizieren. In der Dreisatztabelle ist dies erkennbar am Übergang von der zweiten in die dritte Spalte.

Bezeichnen wir nun die Zeit mit $x$ und die Strecke mit $y$, so schließen wir aus der mittleren Spalte:

$y = 50\cdot x$

Wir haben damit ein Beispiel für eine Gleichung einer proportionalen Funktion erhalten.

Darstellungen proportionaler Funktionen

Wie oben bereits festgestellt, lassen sich proportionale Funktionen mit Hilfe von Funktionsgleichungen beschreiben.

Wir betrachten wieder das obige Beispiel, das wir mit folgender Funktionsgleichung beschreiben:

$y = 50\cdot x$

Setzen wir für die Variable $x$, welche hier für die Zeit in Stunden steht, unterschiedliche Werte ein, erhalten wir für jeden $x$-Wert den zugehörigen $y$-Wert. Dieser beschreibt dann die Strecke in Kilometern, die nach dieser Zeit zurückgelegt wird. Die so erhaltenen Zahlenpaare schreiben wir in eine Wertetabelle:

Übertragen wir nun die Wertepaare aus der Tabelle in ein Koordinatensystem, so erhalten wir den Graphen der Funktion:

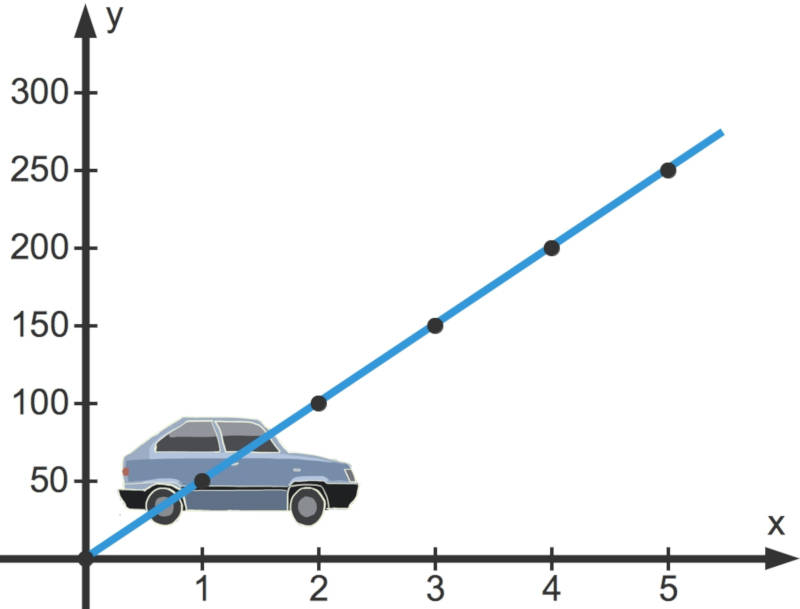
Steigung $m$

Allgemein ist eine proportionale Funktion eine Funktion mit einer Funktionsgleichung der Form $y = m\cdot x$. Der Graph einer proportionalen Funktion ist immer eine Gerade durch den Koordinatenursprung.

Um den Graphen zu zeichnen, werden mindestens zwei Punkte benötigt.

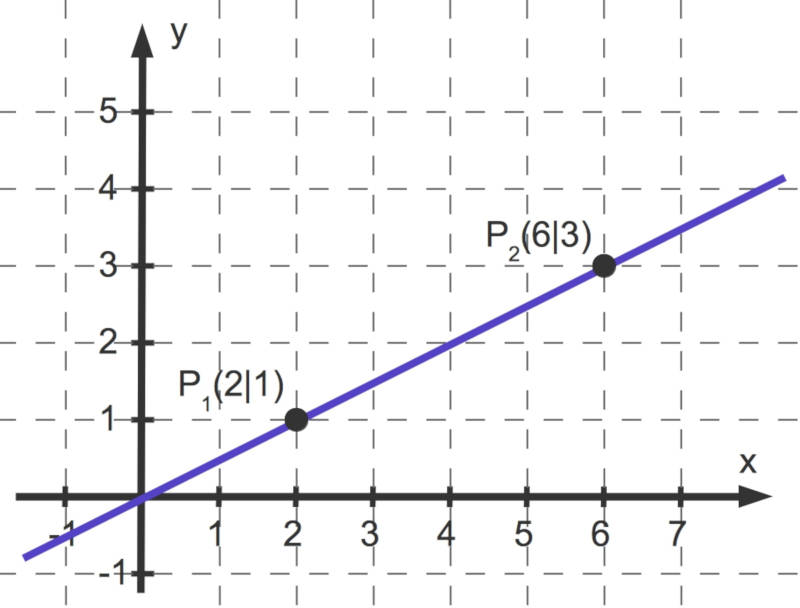
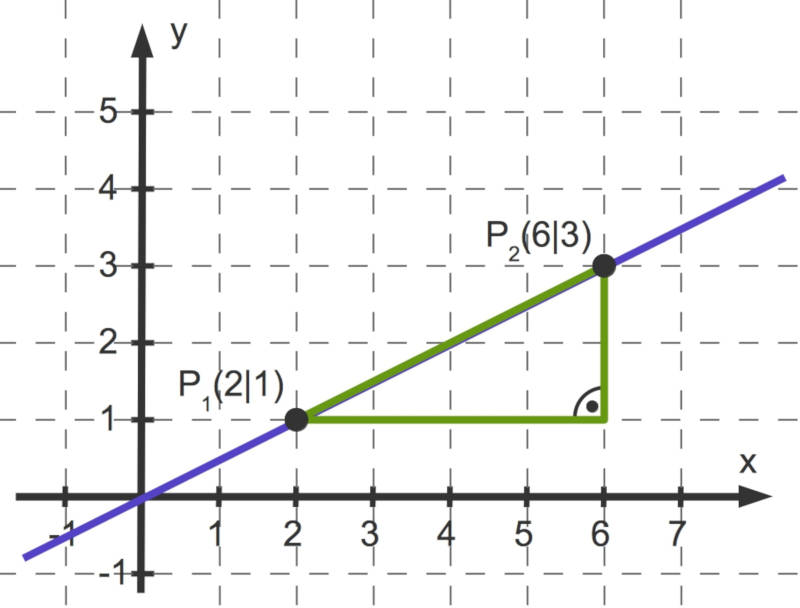
Die Steigung wird mit dem Buchstaben $m$ bezeichnet. In dem Graphen lässt sie sich durch das Steigungsdreieck zwischen $P_1$ und $P_2$ veranschaulichen:

$m = \frac{\text{Anzahl der Einheiten nach oben}}{\text{Anzahl der Einheiten nach rechts}}=\frac{2}{4} = 0,5$

Ist die Steigung positiv, also $m\gt 0$, so handelt es sich wie im obigen Beispiel um eine steigende Gerade:

Bei negativer Steigung, also $m\lt 0$, erhalten wir eine fallende Gerade wie folgt:

Quotientengleichheit

Die Steigung $m$ wird auch Proportionalitätsfaktor genannt.

Wir können $m$ als $\frac{y}{x}$ schreiben und sehen, dass jedes aus der Tabelle eingesetzte Wertepaar das gleiche Ergebnis erzeugt:

$\frac{y}{x} =\frac{-6}{-3} =\frac{-4}{-2} = \frac{-2}{-1} =\frac{2}{1} = 2$

Gleichzeitig erkennen wir hier, dass für $x$ nicht $0$ eingesetzt werden darf, da die Division durch null nicht definiert ist.