Variablen

Inhaltsverzeichnis zum Thema

• Was ist eine Variable?
• Wo kommen Variablen vor?
• Wie können Rechenausdrücke mit Variablen aufgestellt werden?
• Wie können Rechenausdrücke mit Variablen berechnet werden?

Was ist eine Variable?

Wenn dein Opa dir 50 € schenkt und du jeden Monat 5 € sparst, wie viel Geld hast du dann nach 10 Monaten? Richtig: $50~€+10\cdot 5~€=50~€+50~€=100~€$.

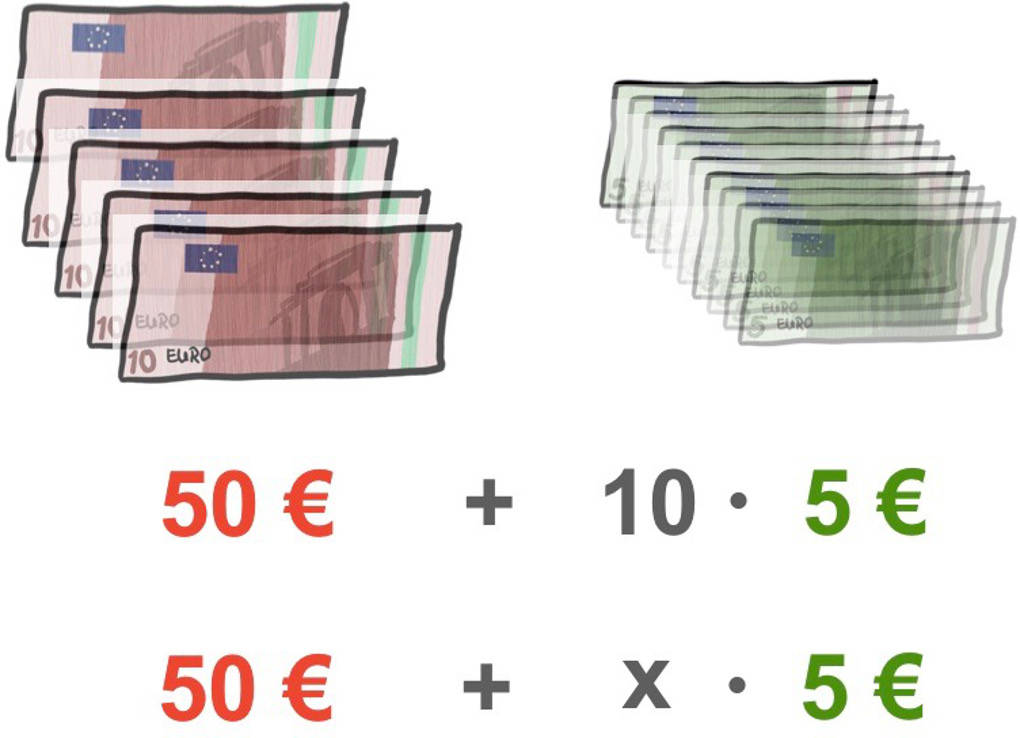
Nun kannst du dich fragen, wie viel Geld du nach 15 Monaten oder nach 24 Monaten oder nach egal wie vielen Monaten gespart hast.

Anstatt immer wieder verschiedene Anzahlen an Monaten zu verwenden, kannst du diese durch eine Variable ersetzen. Eine Variable ist ein Kleinbuchstabe, oft ein $x$. Sie steht als Platzhalter, in diesem Beispiel für die Anzahl der Monate.

Der Begriff der Variable kommt vom lateinischen Adjektiv „variabilis“, welches übersetzt „veränderlich“ bedeutet. Eine Variable kann also auch als Veränderliche bezeichnet werden.

So kannst du in dem obigen Beispiel das Geld, welches du nach einer zunächst unbekannten Anzahl an Monaten, also nach $x$ Monaten hast, mit Hilfe einer Variablen ausdrücken:

$50~€+x\cdot 5~€$

Dieser mathematische Ausdruck wird auch als Rechenausdruck bezeichnet. Für $x$ kannst du jede natürliche Zahl einsetzen.

Mit Variablen kannst du also Zusammenhänge allgemein darstellen.

Wo kommen Variablen vor?

Da eine Variable ein Platzhalter für einen unbekannten, veränderlichen oder besonderen unendlich langen (zum Beispiel $\pi$ oder $e$, hier spricht man dann streng genommen von Konstanten) Wert ist, kannst du eigentlich jeden Buchstaben als Variable verwenden. Dennoch gibt es in der Mathematik einige Konventionen (Vereinbarungen) zum Umgang mit Variablen.

Bei der Beschriftung von Dreiecken nutzt man beispielsweise Kleinbuchstaben als Variablen, um die Seitenlängen zu bezeichnen. Eine Seite wird nach der Konvention genau nach der ihr gegenüberliegenden Punkt bezeichnet. Also liegt dem Punkt $A$ die Seite $a$ gegenüber, dem Punkt $B$ die Seite $b$ und so weiter.

Für die Bezeichnung der Winkel nutzt man hingegen die Kleinbuchstaben des griechischen Alphabets ($\alpha$, $\beta$, $\gamma$, $\delta$, …). Dabei bezeichnet man wiederum die Winkel anhand der Eckpunkte des Dreiecks. Der Winkel $\alpha$ (griechisches "a") wird von den beiden Schenkeln gebildet, die vom Punkt $A$ ausgehen. Der Winkel $\beta$ (griechisches "b") wird von den Schenkeln des Dreiecks gebildet, die vom Punkt $B$ ausgehen und so weiter.

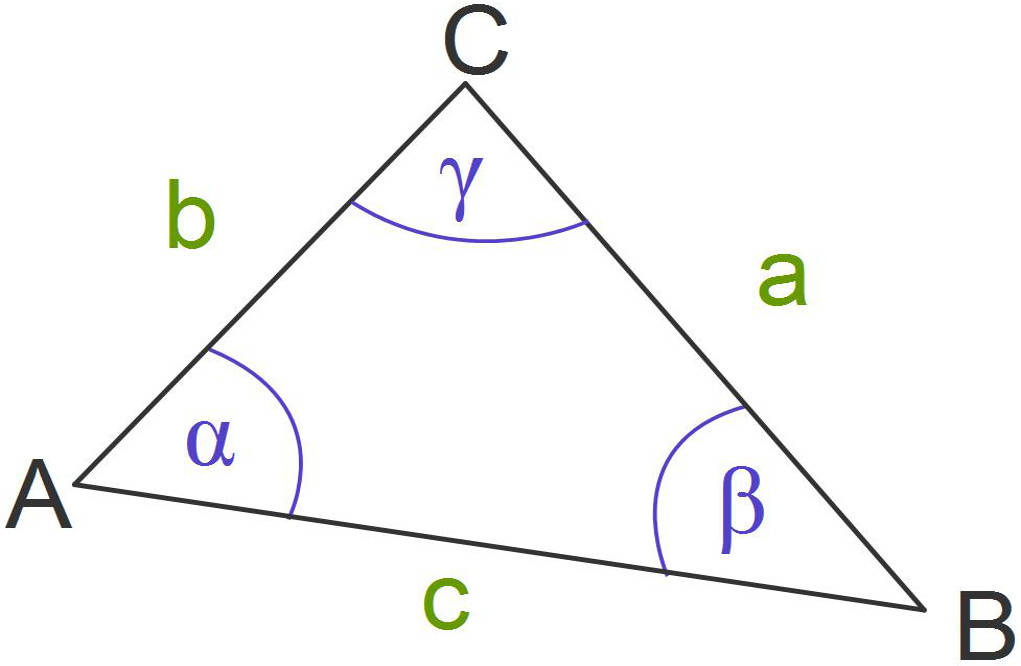
Je nachdem, wie groß die Seiten und Winkel des Dreiecks sind, ändert sich das Aussehen des Dreiecks.

Beim Kreis werden nach der Konvention wieder andere Variablen genutzt. Hierbei werden Variablen entsprechend des Anfangsbuchstabens der im Kreis vorkommenden Längen verwenden. So wird zum Beispiel normalerweise für den Durchmesser des Kreises der Buchstabe $d$, für den Radius der Buchstabe $r$ und für den Umfang ein kleines $u$ verwendet.

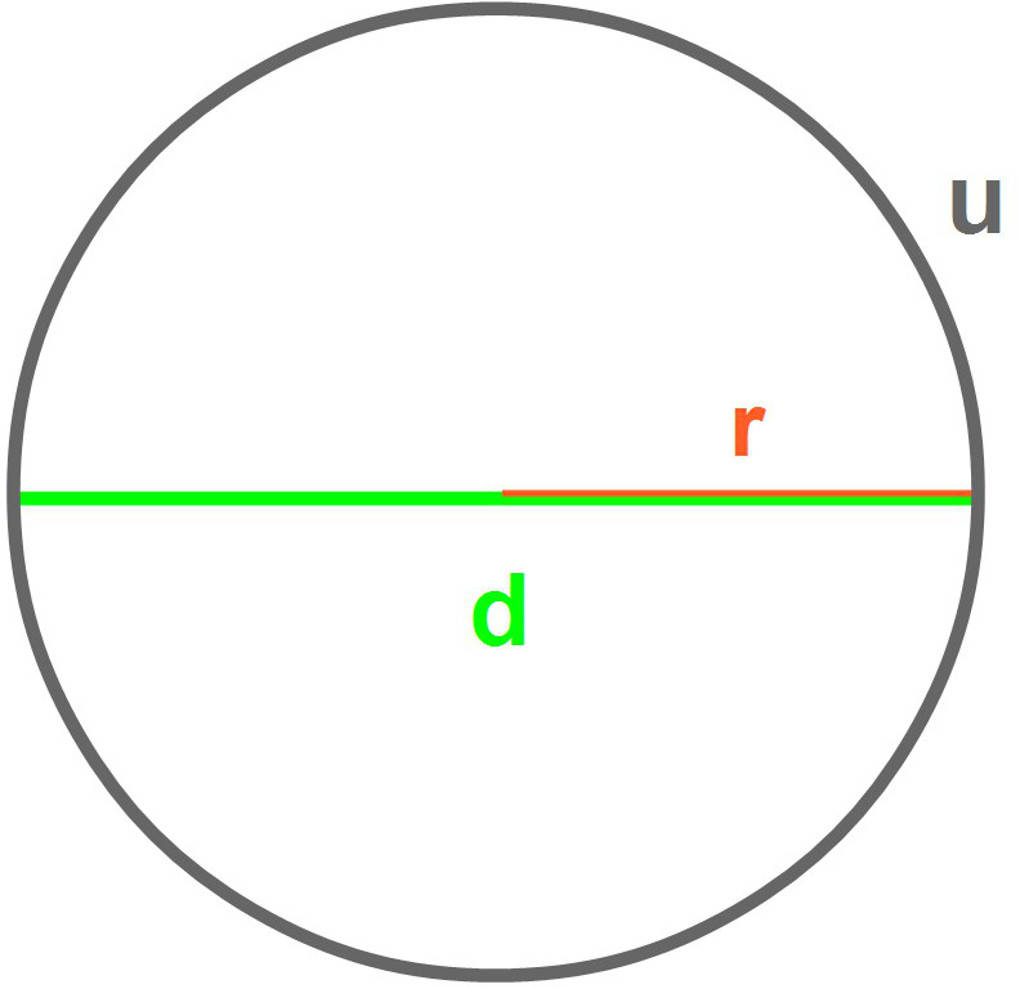
Besonders wichtig sind Variablen für Formeln. Möchtest du zum Beispiel den Flächeninhalt eines Kreises berechnen, so musst du die entsprechende Formel verwenden. Diese lautet:

$A= \pi \cdot r^2$

Für die Berechnung von Flächeninhalten wird gewöhnlich der Großbuchstaben $A$ (vom lateinischen Wort „area“ für Fläche) verwendet. Das Symbol $\pi$ ist hier ebenfalls ein Platzhalter für die irrationale Kreiszahl $\pi=3,141592...$ Die Variable $r$ steht wiederum für den Radius des Kreises.

Wie können Rechenausdrücke mit Variablen aufgestellt werden?

Bei Textaufgaben geht es oft darum, Rechenausdrücke mit Variablen aufzustellen. Ein solcher Rechenausdruck wird auch als Term bezeichnet. Hier zwei Beispiele:

• Lisas Alter ist unbekannt. Ihr Bruder Paul ist 2 Jahre älter als sie. Da du Lisas Alter nicht kennst, verwendest du dafür eine Variable, zum Beispiel $x$. Die Tatsache, dass Paul 2 Jahre älter ist als Lisa, führt zu dem Term für Pauls Alter. Dieser lautet: $x+2$

• Anne und ihre Freunde haben Kuchen gebacken. Sie haben $30~€$ für die Zutaten ausgegeben. Ein Stück Kuchen möchten sie für $1,50~€$ verkaufen. $x$ ist die Anzahl der verkauften Kuchenstücke. Wie lautet der Term, der den Gewinn beim Kuchenverkauf angibt? Der korrekte Term hierfür lautet: $x\cdot 1,50~€-30~€$

Wie können Rechenausdrücke mit Variablen berechnet werden?

Nach dem Aufstellen von Rechenausdrücken, können oft auch Lösungen für diese Ausdrücke berechnet werden. Hier ein Beispiel zum Aufstellen und Lösen von Rechenausdrücken:

Wenn zum Beispiel Anne und ihre Freunde ein Regal für den Klassenraum kaufen wollen, welches $75~€$ kostet, wie viele Stücke Kuchen müssen sie dann verkaufen? Dies führt zu der Gleichung $x\cdot 1,50~€-30~€=75~€$. Was musst du nun für $x$ einsetzen, damit diese Gleichung erfüllt ist?

Um die Gleichung $x\cdot 1,50-30=75$ lösen zu können, musst du die Gleichung nach der Variablen $x$ umstellen.

Zunächst addierst du $30$ auf beiden Seiten der Gleichung:

$\begin{array}{lcll} x\cdot 1,50-30&=&75 &\vert +30\\ x\cdot 1,50-30 \color{#669900}{+30}&=&75 \color{#669900}{+30} &~\\ x\cdot 1,50 &=& 105 &~ \end{array}$

Dann und dividierst du durch $1,50$:

$\begin{array}{lcll} x\cdot 1,50&=&105 &\vert :1,50\\ x\cdot 1,50 \color{#669900}{: 1,50}&=&105 \color{#669900}{:1,50} &~\\ x &=& 70 &~ \end{array}$

Du kannst jetzt eine Probe durchführen, um zu überprüfen, ob du richtig gerechnet hast. Dafür setzt du für $x$ die gefundene Lösung $70$ in der Gleichung ein. Du erhältst $70\cdot 1,50~€-30~€=75~€$. Die Gleichung ist erfüllt und somit ist die Lösung richtig und der korrekte Wert für die Variable gefunden.