Grundbegriffe der Geometrie
Die Geometrie ist ein Teilgebiet der Mathematik. Hier lernst du verschiedene Begriffe oder Elemente der Geometrie kennen.
Beliebteste Videos
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Der Punkt
Der erste Grundbegriff der Geometrie ist der Punkt. Ein Punkt hat keine Ausdehnung, er besitzt also keine Fläche. Häufig wird ein Punkt mit einem kleinen Kreis markiert, doch Vorsicht: Ein Kreis ist wieder ein ganz anderes geometrisches Element. Im Gegensatz zu einem Punkt hat ein Kreis einen Radius und schließt eine Fläche ein. Außerdem kann man einen Punkt auch mit einem kleinen $x$ markieren.
In der Geometrie hat man sich darauf geeinigt, geometrische Figuren, Formen und Elemente nach festen Regeln zu benennen. Punkte werden üblicherweise mit Großbuchstaben $A$, $B$, $C$, ... bezeichnet.
Die Gerade
Ein anderer Grundbegriff der Geometrie ist die Gerade. Eine Gerade sieht aus wie ein Strich, allerdings ist eine Gerade unendlich lang, sie hat also keinen Anfangs- und auch keinen Endpunkt. Wenn du also eine Gerade in dein Heft zeichnest, zeichnest du immer nur einen Ausschnitt der Geraden, eigentlich geht sie nämlich noch weiter. Sie ist länger als dein Heft, dein Zimmer, deine Stadt, ja sogar länger als die Erde.
Dafür kann eine Gerade durch zwei Punkte eindeutig beschrieben werden. Zeichnest du zwei Punkte und verbindest diese miteinander, kannst du die Gerade eindeutig bis in die Unendlichkeit weiter zeichnen. Geraden werden in der Geometrie üblicherweise mit Kleinbuchstaben $g$, $h$, $l$, ... bezeichnet.
Hier siehst du in grün eingezeichnet die Gerade $g$, welche durch die Punkte $A$ und $B$ verläuft.
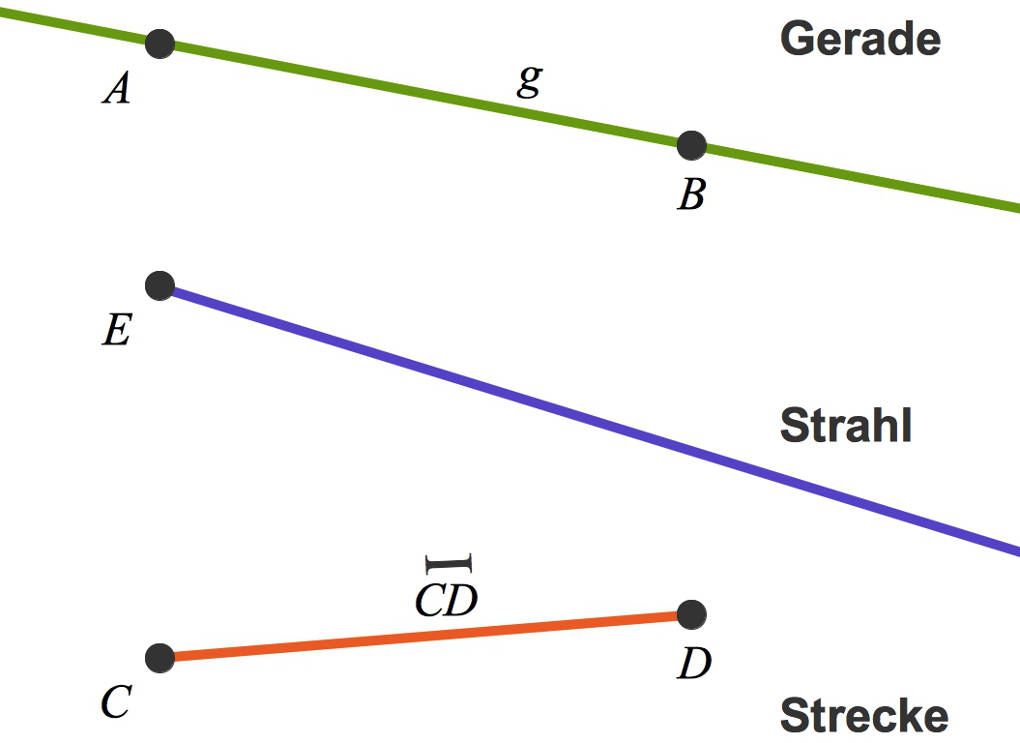
Der Strahl
Unter der Geraden siehst du einen Strahl (blau). Im Gegensatz zu einer Geraden beginnt ein Strahl in einem Punkt und ist nur in die andere Richtung unendlich lang. Strahlen werden auch oft als Halbgeraden bezeichnet. Den Zahlenstrahl hast du bereits kennengelernt oder wirst ihn noch kennenlernen.
Die Strecke
Ganz unten siehst du eine Strecke (rot): Diese verbindet die beiden Punkte $C$ und $D$. Eine Strecke hat also einen Anfangs- und einen Endpunkt. Im Gegensatz zur Geraden und zur Strecke ist sie nicht unendlich lang. Man kann die Länge einer Strecke also messen, sie könnte zum Beispiel $2cm$ lang sein. Eine Strecke ist immer die kürzeste Verbindung zwischen zwei Punkten. Strecken werden, wie in dem Bild zu erkennen, mit dem Anfangs- und Endpunkt sowie einem Strich darüber gekennzeichnet, also zum Beispiel so: $\overline{CD}$.
Winkel
Zwei Strahlen schließen einen Winkel ein. Der gemeinsame Anfangspunkt $S$ der Strahlen wird Scheitelpunkt des Winkels genannt. Winkel werden in der Geometrie mit griechischen Kleinbuchstaben $\alpha$ (alpha für a), $\beta$ (beta für $b$), $\gamma$ (gamma für $c$) ... bezeichnet. Mit Hilfe von Winkeln kann man die Lage zweier Geraden, Strahlen oder Strecken zueinander beschreiben. Wie weit ein Winkel geöffnet ist, wird meistens in Grad gemessen. Das Zeichen dieser Einheit ist der kleine Kreis, zum Beispiel so: $90^\circ$ oder gesprochen ” neunzig Grad”.
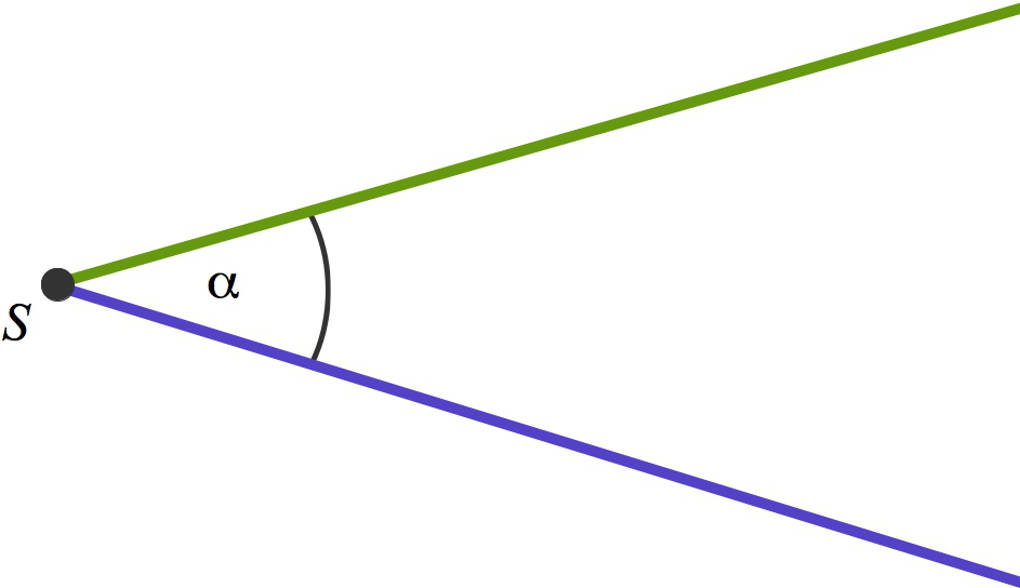
Du unterscheidest verschiedene Winkel:
- Der Nullwinkel beträgt $0^\circ$.
- Ein spitzer Winkel ist größer als $0^\circ$ und kleiner als $90^\circ$.
- Der $90^\circ$-Winkel wird auch rechter Winkel genannt.
- Ein stumpfer Winkel ist größer als $90^\circ$ und kleiner als $180^\circ$.
- Der $180^\circ$-Winkel wird als gestreckter Winkel bezeichnet.
- Jeder Winkel größer als $180^\circ$ und kleiner als $360^\circ$ wird überstumpf genannt.
- Der $360^\circ$-Winkel wird als Vollwinkel bezeichnet.
Der Abstand
Der Abstand zweier geometrischer Elemente, du kennst ja nun bereits einige, ist die kürzeste Entfernung dieser Elemente. Du kannst diesen Abstand zum Beispiel mit einem Lineal oder Geodreieck messen.
Zum Beispiel ist der Abstand zweier Punkte die Länge der Strecke, welche diese beiden Punkte miteinander verbindet. Abstände werden häufig in der Einheit Meter gemessen.
Das Haus vom Nikolaus
Jetzt hast du schon vieles gelernt über geometrische Grundbegriffe, aber was machst du nun mit diesem Wissen? Du könntest das Haus vom Nikolaus zeichnen. Denn dabei verbindest du die Punkte an den Ecken des Hauses mit möglichst wenig Strecken. Die verschiedenen Strecken schließen Winkel ein. Nicht schlecht, oder?
Alle Videos zum Thema
Videos zum Thema
Grundbegriffe der Geometrie (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Grundbegriffe der Geometrie (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebeziehungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Flächeninhalt
- Termumformungen – Übungen
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche gleichnamig machen
- Brüche Multiplizieren
- Brüche multiplizieren – Übungen
- Potenzgesetze
- Distributivgesetz
- Bruchgleichungen lösen – Übungen
- Flächeninhalt Dreieck
- Rationale Zahlen





 Geometrische Grundbegriffe – Überblick
Geometrische Grundbegriffe – Überblick
 Was ist ein Abstand?
Was ist ein Abstand?









