Phasenverschiebung
Erfahre, was eine Phasenverschiebung in der Physik ist und wie man sie berechnet. Die Phasenverschiebung beschreibt die Differenz im Zeitpunkt der Maxima zwischen Schwingungen. Entdecke die Bedeutung von Phasendifferenzen anhand von Beispielen. Interessiert? Das und vieles mehr findest du im folgenden Text!

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Grundlagen zum Thema Phasenverschiebung
Die Phasenverschiebung in der Physik
Hast du schon einmal den Begriff Phasenverschiebung gehört? Er taucht insbesondere dann auf, wenn es um Schwingungen geht – akustische, elektromagnetische oder auch mechanische. Wir wollen uns im Folgenden damit beschäftigen, was eine Phasenverschiebung ist und wie man sie berechnen kann.
Phasenverschiebung – Definition
Um zu verstehen, was eine Phasenverschiebung ist, betrachten wir die folgenden periodischen Schwingungen:
Beide Schwingungen haben dieselbe maximale Amplitude $\hat{A}$ und dieselbe Periodendauer $T$. Das bedeutet, dass bei beiden Schwingungen der Abstand zwischen zwei Maxima gleich ist – für Maxima entspricht er gerade der Periodenlänge $T$ und für Nulldurchgänge der halben Periodenlänge, also $\frac{T}{2}$.
Allerdings erreichen die beiden Schwingungen ihre Maxima zu unterschiedlichen Zeitpunkten. Oder, anders ausgedrückt: Wenn wir die beiden Schwingungen zu einem festen Referenzzeitpunkt $t_{ref}$ betrachten, haben sie unterschiedliche Auslenkungen. Da man die Auslenkung einer Welle auch als ihre Phase bezeichnet, kann man auch sagen: Die beiden Wellen haben eine Phasenverschiebung oder eine Phasendifferenz zueinander. Manchmal wird auch der Begriff Phasenlage verwendet.
Im Allgemeinen können für die Betrachtung der Phasendifferenz zwei Schwingungen auch unterschiedliche Amplituden haben – entscheidend ist, dass sie dieselbe Periodizität haben. Das ist dann der Fall, wenn sie dieselbe Periodenlänge haben, wie in den folgenden Beispielen. Es ist aber auch möglich, dass die Periodenlänge einer Schwingung ein ganzzahliges Vielfaches der Periodenlänge der anderen Schwingung ist, zum Beispiel die doppelte. Auch dann haben diese Schwingungen dieselbe Periodizität.
Phasenverschiebung berechnen
Wenn wir eine sinusförmige Schwingung betrachten, wird die Phase der Schwingung als Summand im Argument der Sinus- oder Kosinusfunktion angegeben. Sie wird in der Regel mit $\phi$ bezeichnet:
$f(x) = \hat{A} \cdot \sin (\omega t + \phi)$
Dabei ist $\hat{A}$ die Amplitude, also die maximale Auslenkung, $\omega$ die Frequenz der Schwingung und $t$ die Zeit. Die Phasenverschiebung zwischen zwei sinusförmigen Schwingungen gleicher Frequenz beziehungsweise Periodendauer ist die Differenz ihrer Phasen $\phi$. Betrachten wir beispielsweise die Schwingungen:
$f(x) = \hat{A} \cdot \sin (\omega t + \phi_f)$
$g(x) = \hat{B} \cdot \sin (\omega t + \phi_g)$
Dann ist die Phasenverschiebung $\Delta \phi$ über die folgende Formel gegeben:
$\Delta \phi = \phi_f - \phi_g$
Die Phase einer Schwingung wird in der Physik in der Regel im Bogenmaß, seltener im Gradmaß angegeben. Die Phasendifferenz liegt dann in derselben Einheit vor.
Bogenmaß
Im Bogenmaß entspricht ein Umlauf, also eine Periode, einer Schwingung, $2 \pi$. Wenn der Schwingungsvorgang im Bogenmaß berechnet wird, wird auch die Phase im Bogenmaß angegeben.
$\sin (\omega t) = \sin (\omega t + 2\pi) \Rightarrow 0 \leq \Delta \phi \leq 2\pi$
Gradmaß
Im Gradmaß entspricht ein Umlauf, also eine Periode, einer Schwingung, $360^{\circ}$. Wenn der Schwingungsvorgang im Gradmaß berechnet wird, wird auch die Phase in Grad angegeben.
$\sin (\omega t) = \sin (\omega t + 360^{\circ}) \Rightarrow 0 \leq \Delta\phi \leq 360^{\circ}$
Phasenverschiebung – Beispiele
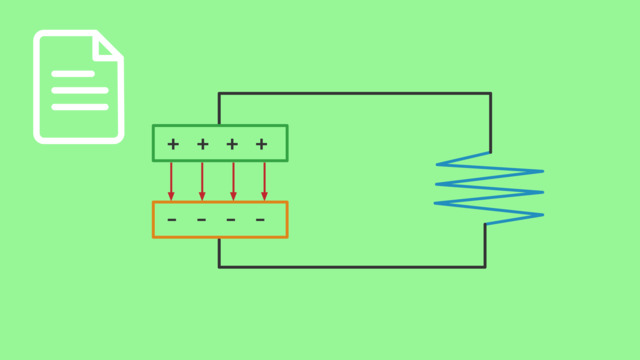
Wir wollen uns noch ein paar Beispiele zur Phasenverschiebung anschauen. Dazu betrachten wir das Verhalten von Wechselstrom und Wechselspannung an verschiedenen Bauteilen.
Ganz oben sehen wir den Strom- und Spannungsverlauf an einem ohmschen Widerstand $\Omega$. Strom und Spannung weisen zwar unterschiedliche maximale Amplituden auf, haben aber zu jedem Zeitpunkt die gleiche relative Auslenkung – die Maxima der beiden Schwingungen finden jeweils zu gleichen Zeitpunkten statt. Sie haben also die gleiche Phase, die Phasendifferenz ist null. Man sagt auch, Strom und Spannung sind gleichphasig:
$\Delta \phi_{\Omega} = 0$
In der Mitte sind Strom- und Spannungsverlauf an einem Kondensator $C$ aufgetragen. Hier sind diese beiden Größen nicht gleichphasig. Bei $\omega t = \frac{\pi}{2}$ erreicht die Spannung beispielsweise ihr Maximum, während die Stromstärke einen Nulldurchgang aufweist. Die Größe der Phasenverschiebung können wir am einfachsten ablesen, indem wir den Abstand zwischen den Nulldurchgängen von Strom und Spannung bestimmen. In diesem Fall gilt:
$\Delta \phi_{C} = \frac{\pi}{2}$
Im Gradmaß entspricht das $90^{\circ}$. Man sagt auch: Der Strom eilt der Spannung voraus.
Ganz unten sind Strom- und Spannungsverlauf an einer Spule $L$ aufgetragen. Auch hier sehen wir, dass beide Größen eine Phasenverschiebung aufweisen. Durch Ablesen der Nulldurchgänge können wir die Phasenverschiebung bestimmen:
$\Delta \phi_{L} = -\frac{\pi}{2}$
Im Gradmaß entspricht das $-90^{\circ}$. Man sagt auch: Der Strom hinkt der Spannung hinterher.
Transkript Phasenverschiebung
Hallo und herzlich willkommen zu Physik mit Kalle. Wir wollen uns heute aus dem Gebiet Schwingungen und Wellen mit der Phasenverschiebung beschäftigen. Für dieses Video solltet Ihr bereits den Film zum Wechselstrom gesehen haben. Wir lernen heute, was Phasenverschiebung ist, wie man sie beschreiben kann und als Beispiel, wie sie am ohmschen Widerstand, am Kondensator und an der Spule im Wechselstromkreis aussieht. Zwischen zwei Sinusschwingungen besteht eine Phasenverschiebung, die man delta Phi nennt, wenn sie die gleiche Periodendauer T haben, ihre Maxima jedoch zu unterschiedlichen Zeitpunkten erreichen. Wir erinnern uns, die Formeln für die momentanen Werte von sinusförmiger Wechselspannung oder sinusförmigen Wechselstrom waren u(t)=Scheitelspannung ×sin Omega t+PHIu und für den Strom I(t)=Scheitelstrom ×sin Omega t+PHIi. PHIu und PHIi sind die Phasen von Spannung und Strom. Denn nur weil die beiden sinusförmig sind, heißt es ja noch lange nicht, das sie genau wie der Sinus bei 0 anfangen. Delta PHIi, also die Differenz der beiden Phasen, nenne ich die Phasenverschiebung. Ihr seht leicht, ist PHIu=PHIi ist die Phasendifferenz 0 und damit liegt keine Phasenverschiebung vor. Man sagt dann, Strom und Spannung sind in Phase. Im Bild unten könnt Ihr mehrere gegeneinander phasenverschobene Sinusschwingungen sehen. Wenn Ihr die beiden Hilfslinien beachtet, die genau im Abstand einer Periodendauer eingezeichnet sind, erkennt Ihr schnell, alle diese Schwingungen haben die gleiche Periodendauer. Die Wellenberge sind jedoch überall woanders. Das heißt, sie sind alle gegeneinander phasenverschoben. Wie man diese Phasenverschiebung nun beschreiben kann, das wollen wir uns im nächsten Kapitel ansehen. Eine Sinusschwingung kann man sich ja irgendwie als einen sich ständig wiederholenden Umlauf auf einer Kreislinie vorstellen. Falls Ihr Probleme habt, das zu verstehen, keine Panik, dazu kommt gleich noch eine Animation. Wir erinnern uns aber erst mal, wir haben zwei verschiedene Möglichkeiten den Winkel anzugeben, der uns sagt, wo wir uns auf dem Kreis befinden. Die erste Möglichkeit ist das Bogenmaß. Im Bogenmaß steht 0 für 0° und 2TT für 360°. Da sich mein Kreisumlauf ja alle 2TT wiederholt, kann ich also aufschreiben sin(Omega t)=sin(Omega t+2TT). Meine Phasenverschiebung muss also irgendwo zwischen 0 und 2TT liegen. Im Gradmaß wiederholt sich ein Kreisumlauf natürlich nach 360°. Ich kann also aufschreiben sin(Omega t)=sin(Omega t+360°). Das heißt, das in Gradmaß meine Phasenverschiebung zwischen 0° und 360° liegen muss. Die dritte Möglichkeit könnt Ihr gut im Bild unten erkennen. Meine Sinusschwingung benötigt die Periodendauer groß T, um eine vollständige Schwingung auszuführen. Ich kann also meine Phasenverschiebung auch als Bruchteil von T angeben. Sie muss dann irgendwo zwischen 0 Sekunden und groß T liegen. Wie merken uns also, man gibt die Phasenverschiebung normalerweise im Bogenmaß, im Gradmaß oder als Bruchteil der Periodendauer T an. Weil sie sowohl die Sinusschwingung als Kreisumlauf, als such die Phasenverschiebung im Gradmaß besonders schön erklärt, will ich Euch noch kurz eine Animation von einem der 3 Beispiele, die wir uns gleich ansehen wollen, zeigen. In der Animation links könnt Ihr den Verlauf von Strom und Spannung an einem Kondensator beobachten. Wie Ihr seht, eilt der Strom der Spannung voraus. Es besteht also eine Phasenverschiebung, die wir mit Hilfe der beiden eingezeichneten Pfeile sehr leicht ablesen können. Delta PHI ist TT/2. Das entspricht auch 90° oder einem 1÷4 der Periodendauer T. Es ist übrigens auch möglich, der Vollständigkeit halber, eine Phasendifferenz zu erhalten, wenn ich zwei Schwingungen von verschiedenen Quellen mit gleicher Periodendauer aussende. Falls die eine Schwingung zu einem bestimmten Ort einen längeren Weg zurück zulegen hat als die andere, entsteht dort durch diesen Gangunterschied eine Phasendifferenz. Dieser Fall wird in den Videos über Indifferenz ausführlich behandelt. Falls Ihr Euch also dafür interessiert bitte seht dort nach. Zum Schluss wollen wir uns jetzt den Spannungs- und Stromverlauf am ohmschen Widerstand, am Kondensator und an der Spule ansehen. Die ich hier einfach mit R,L und C abkürze. Denn im Wechselstromkreis nennt man eine Spule einen induktiven und einen Kondensator einen kapazitiven Widerstand. Messe ich Strom und Spannung an einem ohmschen Widerstand im Wechselstromkreis, so erhalte ich diesen Verlauf. Wir sehen die 0 Durchgänge und die Maxima und Minima geschehen bei beiden zur selben Zeit. Die beiden sind also in Phase. Das heißt, es liegt keine Phasenverschiebung vor, Delta PHI ist also 0. Beim Kondensator, denn wir ja gerade schon in der Animation gesehen hatten, sieht der Verkauf so aus. Der Strom eilt der Spannung voraus. Wir haben also eine Phasenverschiebung. Und sie beträgt Delta PHI = TT/2 oder 90° oder T/4. Messen wir den Verlauf von Spannung und Strom an einer Spule, so ergibt sich folgendes Bild. Der Strom hinkt diesmal der Spannung hinterher, und zwar um den gleichen Betrag, den er beim Kondensator vorausgeeilt war. Die Phasenverschiebung Delta PHI ist also -TT/2 oder -90° oder -T/4. Da sich der Sinus ja mit jeder Periode wiederholt, kann ich diese nicht so schönen, negativen Phasenverschiebungen einfach umwandeln, indem ich eine Periode dazuzähle. Ich kann also auch schreiben Delta PHI=-TT/2+2TT oder 3TT/2 und das entspricht 270° oder 3T/4. Wir wollen noch mal wiederholen, was wir heute gelernt haben. Zwischen 2 Sinusschwingungen besteht eine Phasenverschiebung, wenn sie die gleichen Periodendauer T haben, ihre Maxima jedoch zu unterschiedlichen Zeitpunkten erreichen. Man kann die Phasenverschiebung Delta PHI auf unterschiedliche Weisen angehen. Im Bogenmaß, sie liegt dann zwischen 0 und 2TT, im Gradmaß, dann muss sie zwischen 0° und 360° liegen und als Bruchteil der Periodendauer, dann liegt sie zwischen 0 Sekunden und der Periodendauer groß T. Negative Phasendifferenzen kann man leicht in positive verwandeln, indem man einfach eine komplette Periode dazu addiert. Zum Beispiel im Gradmaß -90°=-90°+360°=270°. Und im Bogenmaß -TT/2=-TT/2+2TT=3TT/2. So, das war es schon wieder für heute. Ich hoffe ich konnte Euch helfen? Vielen Dank fürs Zuschauen vielleicht bis zum nächsten Mal. Euer Kalle.
Phasenverschiebung Übung
-
Gib die richtige mathematische Darstellung der Phasenverschiebung an.
TippsSowohl $\Delta \varphi$ als auch $\varphi_u$ und $ \varphi_I$ sind Winkel.
Die Phasenverschiebung könnte man auch als Phasendifferenz bezeichnen.
LösungDer Unterschied der Phasen der einzelnen Schwingungen wird mittels deren Differenz angegeben.
Für den Phasenunterschied gilt also : $\Delta \varphi = \varphi_u - \varphi_I$.
Wir betrachten dabei zwei Schwingungen mit gleicher Schwingungsdauer $T$. Die Indices beziehen sich auf die Bezeichnungen der Schwingungen. Hier betrachten wir demnach eine Schwingung $U(t)$ im Verhältnis zu einer Schwingung $I(t)$.
Im Weiteren wollen wir uns einmal überlegen, welche Sonderfälle auftreten können.
Ist die Phasenverschiebung ganzzahlig, so treten immer zu gleichen Zeitpunkten $t$ die Amplituden der Schwingungen auf. Der Unterschied besteht hier darin, dass die Schwingungen ihre Maxima unterschiedlich oft durchlaufen haben, denn eine der beiden muss später gestartet sein.
Ergibt sich für die Phasenverschiebung $ 0,5 + n$, so finden wir immer dann ein Maximum bei der einen Schwingung, wenn die andere ein Minimum durchläuft.
Diese beiden Sonderfälle sind meist leicht an der grafischen Darstellung nachzuvollziehen.
-
Gib an, wann eine Phasenverschiebung vorliegt.
TippsDie Schwingungen müssen vergleichbar sein.
Die Periodendauern müssen daher gleich sein.
LösungZwischen zwei Sinusschwingungen besteht eine Phasenverschiebung $\Delta \varphi$, wenn sie die gleiche Periodendauer $T$ haben, ihre Maxima jedoch zu unterschiedlichen Zeitpunkten erreichen.
Damit wir von einer Phasenverschiebung reden können, müssen wir also zunächst sicherstellen, dass die verglichenen Schwingungen die gleiche Periodendauer $T$ haben. Wäre dies nicht der Fall, so könnten wir diese nicht vergleichen und keine Aussage über die Verschiebung der Phasen treffen.
Ist dieses Kriterium erfüllt, müssen wir betrachten, zu welchen Zeitpunkten $T$ die unterschiedlichen Schwingungen ihre Maxima erreichen. Der Unterschied zwischen den Zeitpunkten, zu denen diese erreicht werden, wird als Phasenverschiebung bezeichnet.
Stelle dir hier zwei Schaukeln vor. Auf beiden Schaukeln sitzt jeweils ein Kind. Das Schwingverhalten der Schaukeln sei zudem gleich, sodass beide die gleiche Periodendauer haben. Lenken wir nun eine Schaukel nach vorne und eine nach hinten aus, so sind die Schwingungen zwar ähnlich jedoch nicht identisch. Immer wenn eine der beiden Schaukeln ihre maximale Auslenkung nach vorne erfährt, ist die andere maximal nach hinten ausgelenkt. Sie sind also phasenverschoben. Um dieses Gedankenexperiment nun physikalisch korrekt und vollständig zu erfassen, muss diese Tatsache mittels der Phasenverschiebung berücksichtigt werden.
-
Untersuche die mathematischen Darstellungen der Schwingung.
TippsDer Strom eilt der Spannung voraus.
Für $\Delta \varphi $ gilt $90° = \frac{\pi}{2} = \frac{T}{4}$.
LösungDie Phasenverschiebung kann in unterschiedlichen Darstellungen angegeben werden.
Um diese richtig zu verstehen, müssen wir also auch die Umrechnungen nachvollziehen können.
Generell wird unterschieden zwischen der Phasenverschiebung als Funktion der Umlaufdauer in Abhängigkeit des Bogenmaßes sowie der Darstellung im Gradmaß.
In allen Fällen nehmen wir an, dass der Strom der Spannung um $90°$ vorauseilt. Rechnen wir diese um, so ergibt sich $90° = \frac{\pi}{2} = \frac{T}{4}$.
Um nun die passende Schwingung des Stromes seiner Spannung zuzuordnen, müssen wir also $90° = \frac{\pi}{2} = \frac{T}{4}$ addieren, je nachdem, welches Maß angegeben ist.
Betrachten wir ein Beispiel:
Gegeben ist die Schwingung $ U \cdot \sin(\omega \cdot t)$. Der korrespondierende Strom muss nun vorauseilen, also positiv phasenverschoben sein. Die Phasenverschiebung beträgt $ \Delta \varphi = \frac{T}{4}$. So ergibt sich für $I$:
$ I \cdot \sin(\omega \cdot t + \frac{T}{4})$.
-
Bestimme die Phasenverschiebungen zwischen Spannung und Strom.
TippsDie Phasenverschiebung ist unterschiedlich, je nachdem, welches Bauteil betrachtet wird.
Die Phasenverschiebung gibt den zeitlichen Unterschied der Strom- und Spannungsspitzen an.
LösungBetrachtet man die Veränderung der Strom-Spannungs-Phase eines Wechselstroms an unterschiedlichen Bauteilen im Stromkreis, so zeit sich jeweils ein charakteristisches Verhalten.
Wir unterscheiden hier nach Ohm'schem Widerstand, Spule und Kondensator.
Am Ohm'schen Widerstand ist keine Phasenverschiebung zwischen Strom und Spannung zu ermitteln. Hier ist also die $ \varphi = 0$. Dies gilt auch für einen Leiter, der kaum einen elektrischen Widerstand aufweist.
Anders ist es bei der Spule. Hier ist eine Phasenverschiebung von $ \Delta \varphi = \frac{3 \pi}{2} $ zu messen. Das bedeutet, der Strom folgt der Spannung nach
Am Kondensator beträgt die Phasenverschiebung $ \Delta \varphi = \frac{\pi}{2} $ oder $ 90 °$.
Wird kein Bauteil eingebracht, so tritt auch keine Phasenverschiebung auf, und wir müssen diese nicht berücksichtigen.
-
Gib an, wann zwei Schwingungen „in Phase" sind.
TippsEin Phasenunterschied kann auf einem Gangunterschied beruhen.
Zwei Schwingungen sind in Phase, wenn sie stets zeitgleich ihre Maxima erreichen.
LösungZwei Schwingungen sind dann "in Phase", wenn sie einen Gangunterschied von $ \Delta \varphi = 0 $ aufweisen.
Dazu müssen die beiden betrachteten Schwingungen die gleiche Umlaufdauer $T$ haben, da sonst ein Vergleich nicht möglich ist.
Wird etwa ein elektrisches Signal an einem ohm'schen Widerstand verzögert, so stellt sich - im Vergleich zum unbeeinflussten Signal - ein Phasenunterschied ein. Das bedeutet, die Maxima der einzelnen Schwingungen werden zeitverschoben erreicht.
Die Frequenzen müssen entsprechend der Äquivalenz der Umlaufdauer dabei ebenfalls aufeinander abgestimmt sein.
Es liegt ein Vergleich zur Interferenzbedingung nahe: der Kohärenz. Auch hier müssen zwei betrachtete Lichtwellen, die sich als Schwingungen in Zeit und Raum ausbreiten, die gleiche Schwingungsdauer und damit Frequenz haben. Ansonsten wäre eine Vorhersage des Interferenzmusters unmöglich.
-
Gib die Phasenverschiebung im Bogenmaß, Grundmaß und als Anteil der Umlaufdauer an.
TippsEin Kreis hat $ \varphi = 360°$.
Der Kreisumfang beträgt $ 2 \pi$.
LösungUm die Verschiebung der Phasen mathematisch zu beschreiben, kann man unterschiedliche Ansätze nutzen.
Man behilft sich dabei der Tatsache, dass sich die Schwingung analog zur einer Kreisbewegung verhält, so wie etwa der Zeiger einer Uhr. Diesem können wir stehts einen Winkel $\phi$ und ein Bogenmaß in Abhängigkeit von der Kreiszahl $\pi$ zuordnen. Außerdem können wir die Schwingung als einen Bruchteil der gesamten Schwingungsdauer $T$ angeben.
Somit erhalten wir drei unterschiedliche Einheiten, in denen wir die Phasenverschiebung angeben können. So entspricht eine Verschiebung um Winkel $0°$ dem Bogenmaß $0 \pi$ sowie der anteiligen Umlaufdauer von $ 0 T $.
Da wir eine Betrachtung am Kreis machen, reproduziert sich die Schwingung alle $ \varphi = 360°$ oder nach jeder Periode $ 1 T $ sowie nach dem Umlauf der Strecke $ 2 \pi$.
Damit kannst du nun ermitteln, wie du einen Winkel von $180°$ in Anteilen der Periodendauer $ = \frac{T}{2} $ oder dem Bogenmaß $ = \pi$ angibst.
Analog dazu kannst du nun die weiteren Beispiele lösen. Viel Spaß dabei!
9'182
sofaheld-Level
6'600
vorgefertigte
Vokabeln
7'643
Lernvideos
35'607
Übungen
32'360
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie
- Parallelschaltung
- Dopplereffekt, Akustischer Dopplereffekt


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?

















Hallo M Mueller,
vielen Dank für ihr Feedback, es stimmt, dass in der Elektrotechnik und im Physikstudium für die Augenblickswerte (Spannung / Stromstärke) u bzw. i verwendet wird. Wie auch für die Scheitelwerte das û bzw. î.
Jedoch ist dies in der Schule in der Regel nicht der Fall. Hier wird für den Scheitelwert am häufigsten I₀ und U₀ und für die Augenblickswerte U(t) und I(t) verwendet.
Da wir uns an der Schule orientieren, haben wir uns auch für diese Schreibweise entschieden.
Liebe Grüße für die Redaktion.
Sehr schönes Video. Ich möchte allerdings anmerken das die Kenngrößen beim Wechselstrom und Wechselspannung wie z.B. der Augenblickswert oder der Scheitelwert mit kleinen Buchstaben geschrieben werden.
Es wäre schön wenn darauf bei weiteren Videos geachtet werden könnte.
Ansonsten wurde das Thema sehr schön und verständlich erklärt.
Bei der letzten Aufgabe hat sich ein kleiner Fehler eingeschlichen. Dort müsste anstatt pi =360°, 2pi = 360° stehend. Und bei einer Phasenverschiebung fehlt das Grad an der Einheit.
Ansonsten danke für das Video und die Übungen.
Koennt ihr bitte mehr Aufgaben stellen, um das Wissen von den Videos zu benutzen, weil Physik braucht, dass man viele Aufgaben loest, um den Stoff richtig zu verstehen.