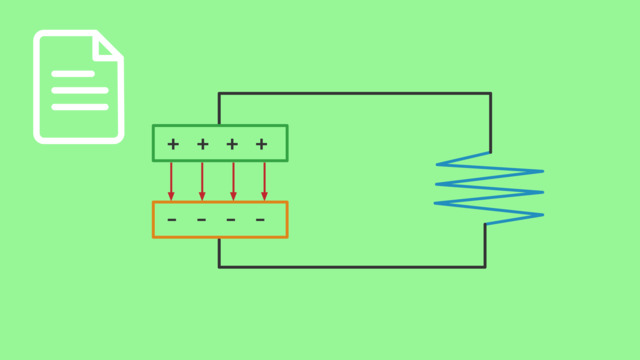
Der thomsonsche Schwingkreis – im Vergleich mit dem Federpendel

Der thomsonsche Schwingkreis – im Vergleich mit dem Federpendel Übung

• Ordne die Bewegung im elektrischen Schwingkreis dem Äquivalent beim Federschwinger zu.

  Tipps

  Du kannst die Bilder mit der 1. bereits miteinander verbinden, dann hast du einen Anfang für die Schwingungsverläufe.

  Lösung

  Elektrischer und mechanische Schwinger verhalten sich im Grunde gleich, allerdings kann man sich den elektrischen oft schwerer vorstellen. Deshalb vergleichen wir hier.

  1. In der Ausgangslage ist der Kondensator geladen, der Massenpunkt ist nach rechts ausgelenkt.

  2. Nun fließt der Strom des Kondensators durch die Spule. Dabei entsteht ein Magnetfeld. Äquivalent dazu beginnt der Massepunkt, sich nach rechts zu bewegen, da die ausgelenkte Feder zurückdrängt, und auch die gestauchte Feder in ihre Ausgangslage möchte.

  3. Die gesamte Energie des elektrischen Stromkreises liegt nun in Form des Magnetfeldes vor. Das entspricht der Ruhelage des Federschwingers, bei dem der Massepunkt gerade mittig in seiner Ruhelage liegt.

  4. Dann wird das Magnetfeld allmählich von der Spule absorbiert, also in elektrische Energie umgewandelt. Beim Federschwinger entspricht das der Schwingung nach links.

  Man könnte sich die Schwingungen in diesem Fall so vorstellen, dass ein Strom nach rechts eine Auslenkung nach rechts ist, und der Rückweg dann die Auslenkung zur anderen Seite.

• Beschreibe die Thomson'sche Schwingungsgleichung.

  Tipps

  $x^{-1}=\dfrac{1}{x}$

  $f=\dfrac{1}{T}$

  Lösung

  Bei der mechanischen Schwingung kann man sich Frequenz und Schwingungsdauer gut vorstellen. Nicht so beim elektrischen Oszillator.

  Man kann sich ja sicher schon denken, dass die Frequenz etwas mit der Spule und dem Kondensator zu tun hat. Deren Haupteigenschaften sind die Kapazität (des Kondensators) und die Induktivität (der Spule).

  Die Kreisfrequenz $\omega$ ist allgemein gegeben durch $2\pi$ mal der Frequenz $f$.

  Dies stellt man das nach $f$ um:

  $f=\dfrac{\omega}{2\pi}$.

  Wieso nun $\omega=\dfrac{1}{\sqrt{L\cdot C}}$, ist etwas komplizierter. Setzt man das ein, ergibt sich die Thomson'sche Schwingungsgleichung:

  $f=\dfrac{1}{2\pi\cdot\sqrt{L\cdot C}}$.

  Und weil $f=\dfrac{1}{T}$, ist ist die Schwingungsdauer $T=2\pi\cdot\sqrt{L\cdot C}$.

• Beschrifte die Energiezustände im elektrischen Schwingkreis.

  Tipps

  Die Bilder folgen in ihrer Reihenfolge dem zeitlichen Verlauf. So kannst du vielleicht besser einordnen, was passiert.

  Lösung

  Ebenso wie die potentielle und kinetische Energie beim Federschwinger verhält sich die Energie beim elektrischen Schwinger.

  Nur ist es hier eben die elektrische und die magnetische Energie.

  Die magnetische Energie entsteht durch die elektrische Energie in der Spule. Andersherum wird die magnetische Energie dann wieder in elektrische umgewandelt.

  So laufen immer wieder Umwandlungsprozesse ab von elektrischer zu magnetischer Energie und umgekehrt.

• Berechne die Frequenz eines elektrischen Schwingkreises.

  Tipps

  Du benötigst die Thomson'sche Schwingungsgleichung.

  Achte auf die Größenordnungen der Einheiten.

  Lösung

  Die Thomson'sche Schwingungsgleichung ist

  $f=\dfrac{1}{2\pi\cdot\sqrt{L\cdot C}}$.

  Wir setzen ein:

  $f=\dfrac{1}{2\pi\cdot\sqrt{2~\text{H}\cdot 100 \cdot 10^{-6}~\text{F}}}=\dfrac{35,36}{\pi}=11,3~\text{Hz}$.

  Interessanter ist vielleicht, wie wir auf die Einheit $\text{Hz}$, also $\dfrac{1}{\text{s}}$, kommen.

  Nun: 1/ haben wir ja schon, und $2\pi$ hat keine Einheit.

  $L\cdot C$ hat die Einheit $\dfrac{\text{kg}\cdot\text{m}^2}.{\text{A}^2\cdot\text{s}^2}\cdot\dfrac{\text{A}^2\cdot\text{s}^4}{\text{kg}\cdot\text{m}^2}$

  Man kann sehen, dass sich alles rauskürzt und am Schluss nur noch $\text{s}^2$ stehen bleibt. Das erklärt dann auch, warum die Wurzel in der Thomson'schen Gleichung wichtig ist. Denn dadurch wird aus $\text{s}^2$ nur noch $\text{s}$, und wir kommen zur Einheit $\dfrac{1}{\text{s}}$, also $\text{Hz}$.

• Beschreibe den elektrischen Schwingkreis.

  Tipps

  Überlege, was die Haupteigenschaft einer ungedämpften Schwingung ist. Also wie es sich da mit äußeren Kräften verhält.

  Lösung

  Wie läuft dieser elektrische Schwingkreis nochmal ab?

  Zunächst wird ein Kondensator geladen. Ab dann ist er sozusagen die Spannungsquelle für die Spule, die ein Magnetfeld erzeugt, dann aber die magnetische Energie wieder in elektrische Energie umwandelt. Dadurch wird der Kondensator immer wieder entladen, und andersherum gepolt beladen.

  Er wechselt also periodisch seine Polung, während die Spule ein Magnetfeld auf- und abbaut.

  Im Idealfall ginge das endlos hin und her, ohne dass man Energie von außen hinzufügen müsste. In der Realität sieht es aber anders aus.

• Löse die Differenzialgleichung für eine freie ungedämpfte E-Schwingung.

  Tipps

  Die Lösung ist der Ansatz ohne unbekannte Variablen. Du musst den Ansatz also so umschreiben, dass er nur noch Größen enthält, die man (eigentlich) immer kennt.

  Lösung

  Fangen wir also an mit dem Ansatz $Q(t)=Q_0\cdot\cos(\omega\cdot t)$, wobei $Q_0$ die Anfangsladung ist.

  Das können wir erstmal in die DGL einsetzen. Auch die zweite Ableitung von $Q$ sollten wir dort einsetzen. Daher berechnen wir diese zuerst einmal:

  $\dot{Q}(t)=-Q_0\cdot\omega\cdot\sin(\omega\cdot t)$

  $\ddot{Q} (t)=-Q_0\cdot\omega^2\cdot\cos(\omega\cdot t)$.

  Und dann in die DGL eingesetzt:

  $L\cdot \left[-Q_0\cdot\omega^2\cdot\cos(\omega\cdot t)\right] + \dfrac{Q_0\cdot\cos(\omega\cdot t)}{C}=0$.

  Weil das so aber noch etwas hässlich aussieht, schreibt man es um in:

  $Q_0\cdot\cos(\omega\cdot t)\cdot\left[-L\cdot\omega^2+\dfrac{1}{C}\right]=0$.

  Da haben wir jetzt nichts verändert, sondern nur umgestellt. Aber man sieht: Ist der Term in den eckigen Klammern Null, dann geht die Gleichung auf. Klar: Der Kosinus und das $Q_0$ könnten auch Null sein, aber das würde uns nicht zum Ziel führen.

  $-L\cdot\omega^2+\dfrac{1}{C}$ soll nun also $=0$ sein.

  Eine dieser Größen ist uns aus diesem Video bereits bekannt. Aus der Thomson'schen Schwingungsgleichung wissen wir, dass $\omega=\dfrac{1}{\sqrt{L\cdot C}}$ ist.

  $-L\cdot\dfrac{1^2}{\sqrt{L\cdot C}^2}+\dfrac{1}{C}=0$

  Und das stimmt, weil das Quadrat die Wurzel aufhebt , L gekürzt wird und dann dort steht:

  $-\dfrac{1}{C}+\dfrac{1}{C}=0$.

  Also haben wir gezeigt, dass $\omega$ hier tatsächlich die Thomson'sche Formel ist, und wir sie so in unseren Ansatz einsetzen können:

  $Q(t)=Q_0\cdot\cos\left(\dfrac{1}{\sqrt{L\cdot C}}\cdot t\right)$.

  Und das die Lösung der DGL. Nur mit Werten, die wir messen können bzw. kennen, in Abhängigkeit von der Zeit $t$.