Gravitation

Inhaltsverzeichnis zum Thema

• Auswirkung von Gravitationskräften auf der Erde
  • Erdanziehungskraft
  • Ortsfaktor g
  • Gezeiten
• Gravitationsfeld
• Gravitationsgesetz
  • Rechenbeispiel – Gezeitenwirkung der Sonne
  • Rechenbeispiel – Gezeitenwirkung des Mondes
  • Interpretation dieser Werte – die tatsächlichen Auswirkungen auf die Gezeiten
• Gravitation und Weltraum
  • Kepler’sche Gesetze
  • Erste kosmische Geschwindigkeit
  • Zweite kosmische Geschwindigkeit

Auswirkung von Gravitationskräften auf der Erde

Für die Gravitation auf der Erde finden sich viele alternative Benennungen: Erdanziehungskraft, Schwerkraft, „Kraft, die alles nach unten zieht“. Was nicht die Ursache für diese Kraft sein kann, lässt sich leicht bestimmen:

Die Kraft kann nicht magnetischen Ursprungs sein, da in diesem Fall lediglich ferromagnetische Körper angezogen würden.

Die Kraft kann auch nicht elektrischen Ursprungs sein, da in diesem Fall die Kraft, mit der Körper angezogen werden, von deren statischer Aufladung abhängen würde.

Die Ursache der Gravitation ist die Masse selbst. Jede Masse bewirkt eine solche Anziehungskraft.

Erdanziehungskraft

Die Erde ist die größte Masse, die sich in unserem direkten Umfeld befindet. Die Erde besitzt eine Masse von $m_E=5,976 \cdot 10^{24} kg$ und bewirkt damit eine starke Gravitation. Diese Gravitation bewirkt eine Kraft, die jede Masse zum Erdmittelpunkt zieht. Diese Kraft wird daher auch Erdanziehungskraft genannt.

Ortsfaktor g

Die Masse der Erde ist zwar konstant, dennoch wirkt die Erdanziehungskraft nicht überall auf der Erde gleich stark. Je weiter man sich vom Erdmittelpunkt entfernt, desto schwächer wird diese Kraft. So wird man tatsächlich auf dem Mount Everest weniger stark angezogen als am Nordseestrand. Durch die stetige Eigenrotation nimmt der Radius der Erde zum Äquator hin zu. Daher gilt auch: je größer die Entfernung vom Äquator desto größer die Erdanziehungskraft. Diese örtlichen Abhängigkeiten gehen als Ortsfaktor $g$ in die Berechnung jeder Gewichtskraft ein. Bei uns in Deutschland beträgt der Ortsfaktor $g=9,81 \frac{m}{s^2}$. Da mit diesem Ortsfaktor jeder Körper mit Masse zur Erde hin beschleunigt wird, wird diese Größe auch als Fallbeschleunigung bezeichnet.

Gezeiten

Zweimal täglich erleben wir an der Nordsee Ebbe und Flut, das sind die Gezeiten. Diese Wasserstandsveränderung, auch Tide genannt, wird hauptsächlich durch zwei Himmelsgestirne bewirkt: den Mond und die Sonne. Die Gravitationskräfte dieser Himmelskörper werden wie auf der Erde durch den Abstand vom Mittelpunkt der Gestirne und ihre Massen bestimmt. Durch die Massen, die auch noch ständig in Bewegung sind, werden die beweglichen Anteile der Erde wie die Atmosphäre und das Wasser der Meere von den Gestirnen angezogen. Durch diesen Effekt bewegen sich stetig zwei Gezeitenberge um den kompletten Erdball.

Gravitationsfeld

Die Gravitation wird im Modell durch ein Gravitationsfeld um eine Punktmasse dargestellt. Hierbei zeigen die Feldlinien immer in Wirkrichtung, also auf den Schwerpunkt der Punktmasse. Um die Masse herum gibt es nun Positionen, die alle gleich weit entfernt von der Punktmasse sind. Zusammen bilden diese Punkte ein Gravitationspotential in Form eines Ringes um die Punktmasse. Körper auf diesem Potentialniveau würden alle dieselbe Gravitation erfahren.

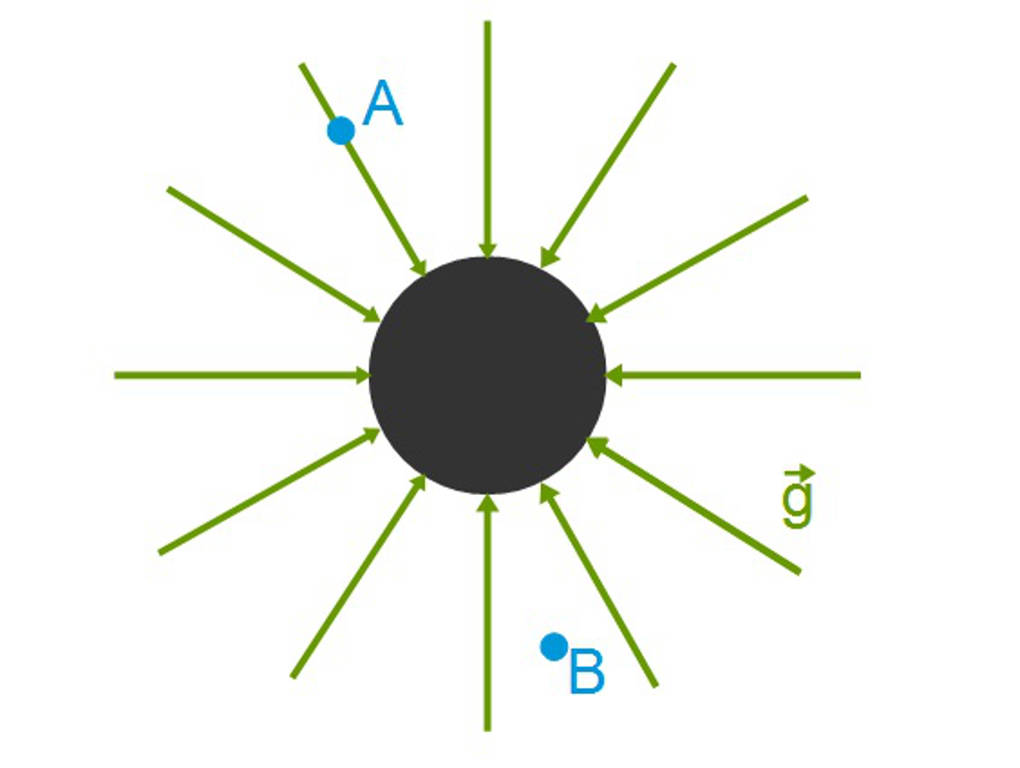
Interessant wird es, wenn eine weitere Punktmasse inklusive Gravitationsfeld in das Feld der ersten Masse eingebracht wird. Nun überlagern sich die Felder und gerade zwischen den Punktmassen heben sich die Gravitationskräfte gegenseitig auf. Im Fall von zwei gleichwertigen Punktmassen wäre genau in der Mitte zwischen den Punktmassen die Anziehungskraft zu beiden Massen gleich groß und das Potential entsprechend Null.

Auf diese Weise lassen sich Phänomene der Gravitation anschaulich zeigen.

Gravitationsgesetz

Mit dem Gravitationsgesetz können die Gravitationskräfte von zwei Massen aufeinander bestimmt werden. Dabei werden die Massen $m_1$ und $m_2$ (in kg) multipliziert und durch das Quadrat des Abstandes $r$ der Massen (in m) zueinander dividiert. Das Quadrat des Abstandes wird gewählt, weil geometrisch die Dichte der Feldlinien beider Massen mit der Entfernung zueinander abnimmt. Das Ergebnis wird dann mit der Gravitationskonstanten $\gamma$ multipliziert.

$F=\gamma \cdot \frac{m_1 \cdot m_2}{r^2}$

mit $\gamma=6,67259\cdot 10^{-11}$

Rechenbeispiel – Gezeitenwirkung der Sonne

Die Sonne hat eine gewaltige Masse von $m_S=2 \cdot 10^{30} kg$. Das ist etwa 335.000 mal so viel wie die Masse der Erde. Dafür ist auch die Entfernung von Sonne und Erde mit $S_S=149,6 \cdot 10^6 km$ sehr groß. Dies entspricht genau einer astronomischen Einheit $1 AE$.

Auf einen Liter Wasser, den wir auf Meereshöhe null finden, würde die Sonne also folgende Gravitationskraft bewirken:

Gegeben: $m_S=2 \cdot 10^{30} kg$, $~m_W=1 kg$, $~S_S=149,6 \cdot 10^6 km$, $~r_E=6378 km$

Gesucht: $F_\text{Sonne}=?$

Ansatz: Wir verwenden das Gravitationsgesetz. Da sich jedoch der Liter Wasser auf Höhe des Meeresspiegels befindet, ziehen wir von der Entfernung einmalig den Erdradius $r_E$ ab.

$\begin{array}{lcl} F_\text{Sonne}&=&\gamma \cdot \frac{m_S \cdot m_W}{(S_S-r_E)^2}\\ &=&6,67259\cdot10^{-11}\frac{m^3}{kg\cdot s^2}\cdot \frac{2 \cdot 10^{30} kg \cdot 1 kg}{(149,6 \cdot 10^6 km-6378 km)^2}\\ &=&6,67259\cdot10^{-11}\frac{m^3}{kg\cdot s^2}\cdot \frac{2 \cdot 10^{30} kg^2}{(148993622 km)^2}\\ &=&6,67259\cdot10^{-11}\frac{m^3}{kg\cdot s^2}\cdot \frac{2 \cdot 10^{30} kg^2}{(148993622000 m)^2}\\ &=&6,67259\cdot10^{-11}\frac{m^3}{kg\cdot s^2}\cdot \frac{2 \cdot 10^{30} kg^2}{2,21991 \cdot 10^{22} m^2}\\ &=&6,67259\cdot10^{-11}\frac{m^3}{kg\cdot s^2}\cdot 9,01 \cdot 10^{7} \frac{kg^2}{m^2}\\ &=&6,01 \cdot10^{-3}\frac{m \cdot kg}{s^2}\\ &=&6,01 \cdot10^{-3} N \end{array} $

Die Sonne bewirkt eine Kraft von $F_\text{Sonne}=6,01 mN$ auf den Liter Wasser auf der Erdoberfläche.

Rechenbeispiel – Gezeitenwirkung des Mondes

Der Mond hat eine deutlich kleinere Masse von $m_M=7,35 \cdot 10^{22} kg$. Damit ist die Erde etwa 81,3 mal so schwer wie der Mond. Dafür ist aber der Mond der Erde auch deutlich näher als die Sonne: Die Entfernung beträgt lediglich $s_M=384400 km$.

Auf einen Liter Wasser, den wir auf Meereshöhe null finden, würde der Mond also folgende Gravitationskraft bewirken:

Gegeben: $m_M=m_M=7,35 \cdot 10^{22} kg$, $~m_W=1 kg$, $~s_M=384400 km$, $~r_E=6378 km$

Gesucht: $F_\text{Mond}=?$

$\begin{array}{lcl} F_\text{Mond}&=&\gamma \cdot \frac{m_M \cdot m_W}{(S_M-r_E)^2}\\ &=&6,67259\cdot10^{-11}\frac{m^3}{kg\cdot s^2}\cdot \frac{7,35 \cdot 10^{22} kg \cdot 1 kg}{(384400 km-6378 km)^2}\\ &=&6,67259\cdot10^{-11}\frac{m^3}{kg\cdot s^2}\cdot \frac{7,35 \cdot 10^{22} kg^2}{(378022 km)^2}\\ &=&6,67259\cdot10^{-11}\frac{m^3}{kg\cdot s^2}\cdot \frac{7,35 \cdot 10^{22} kg^2}{(378022000 m)^2}\\ &=&6,67259\cdot10^{-11}\frac{m^3}{kg\cdot s^2}\cdot \frac{7,35 \cdot 10^{22} kg^2}{1,43\cdot 10^{17} m^2}\\ &=&6,67259\cdot10^{-11}\frac{m^3}{kg\cdot s^2}\cdot 5,14 \cdot 10^{5} \frac{kg^2}{m^2}\\ &=&3,43 \cdot10^{-5}\frac{m \cdot kg}{s^2}\\ &=&3,43 \cdot10^{-5} N \end{array} $

Der Mond bewirkt eine Kraft von $F_\text{Mond}=34,3 \mu N$ auf den Liter Wasser auf der Erdoberfläche.

Interpretation dieser Werte – die tatsächlichen Auswirkungen auf die Gezeiten

Das Gravitationsgesetz betrachtet alle Massen als Punktmasse. Es geht also davon aus, dass die Sonne, der Mond und der Liter Wasser kein Volumen besitzen. Dies ist natürlich in der Natur nicht der Fall. Die Sonne hat zwar eine gewaltige Masse, diese verteilt sich aber auch auf ein gewaltiges, wenn auch sehr dichtes Volumen. Von diesem Volumen steht jedoch nur ein Teil genau senkrecht zur Erde, das bedeutet das auch nur ein kleinerer Teil der Feldlinien die Erde trifft und so auch nur ein kleiner Kraftübertrag stattfindet. Beim Mond sieht das anders aus: Ein großer Teil des Volumens kann als zur Erde senkrecht betrachtet werden. Damit findet hier ein viel besserer Kraftübertrag statt.

Das Resultat der unterschiedlichen Volumina ist, dass der Mond eine etwa doppelt so große Anziehungskraft auf die Erde bewirkt als die Sonne mit ihrer gewaltigen Ausdehnung.

Die Sonne verstärkt jedoch die Gezeiten stark, wenn sie mit dem Mond in einer Reihe zur Erde steht. Diese Konstellation bewirkt dann eine Springflut.

Gravitation und Weltraum

Da sich im Weltraum durch die große Anzahl massereicher Objekte sehr viele Felder überlagern, ist die Anwendung des Gravitationsgesetzes sehr interessant. In jedem Sonnensystem findet sich natürlich eine oder mehrere dominante Massen: die Zentralgestirne. Dabei handelt es sich um einen einzelnen Stern oder einen Pulsar, bestehend aus zwei Zentralgestirnen. Die Bewegungen aller Gestirne eines Systems lassen sich mit Hilfe der Kepler’schen Gesetze berechnen.

Kepler’sche Gesetze

Kepler fand 3 Bedingungen für die Planetenbewegungen: die Kepler’schen Gesetze.

Erstens: Die Planeten bewegen sich auf elliptischen Bahnen, in deren gemeinsamem Brennpunkt die Sonne steht.

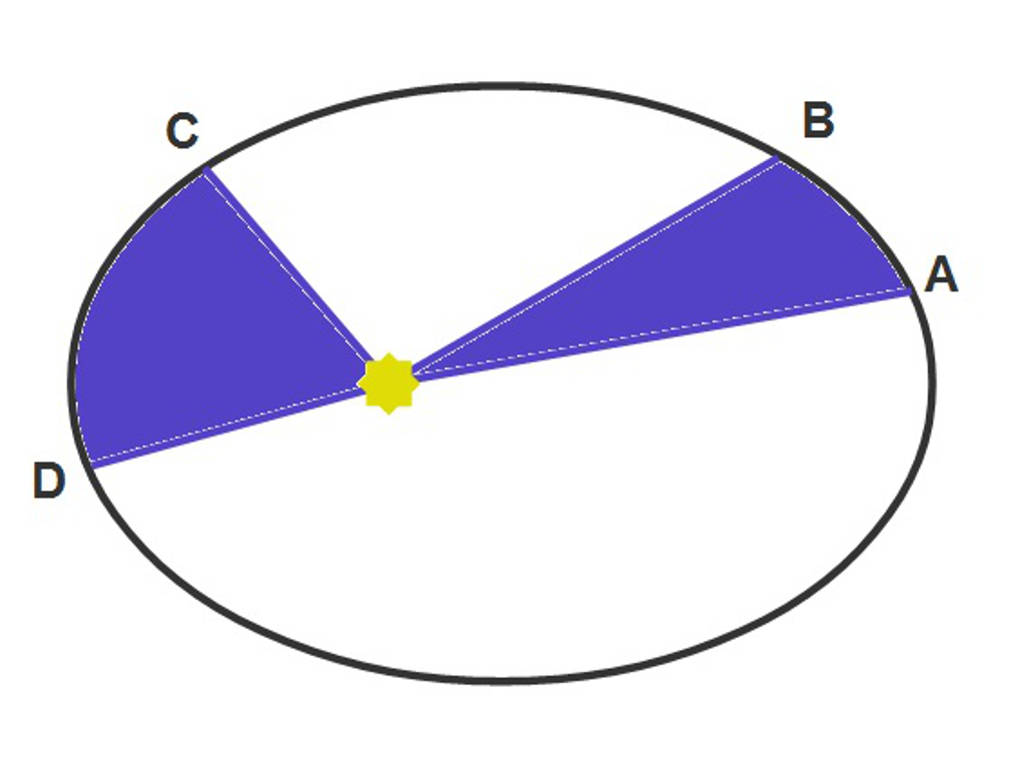
Zweitens: Jeder von der Sonne zum Planeten gezogene Fahrstrahl überstreicht in gleichen Zeiten gleich große Flächen.

$\frac{\Delta A}{\Delta t}=\text{konst.};~ \frac{\Delta A_1}{\Delta t_1}=\frac{\Delta A_2}{\Delta t_2}$

Drittens: Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die Kuben der großen Bahnhalbachsen.

$\frac{T_1^2}{T_2^2}=\frac{a_1^3}{a_2^3}$

Erste kosmische Geschwindigkeit

Die erste kosmische Geschwindigkeit gibt an, wie schnell ein Objekt sein müsste, um sich direkt auf der Erdoberfläche auf einer stabilen Kreisbahn zu bewegen. Hierbei werden natürlich Reibungsverluste ignoriert. Um sich auf einer solchen Kreisbahn zu bewegen, müsste der Körper folgende Geschwindigkeit $v_K$ besitzen:

$v_K=\sqrt{\gamma\frac{m_E}{r_E}}=7,92 \frac{km}{s}$

Zweite kosmische Geschwindigkeit

Die zweite kosmische Geschwindigkeit gibt an, wie schnell ein Objekt sein muss, um dem Gravitationsfeld der Erde gerade so zu entfliehen. Diese Geschwindigkeit $v_p$ berechnet sich über:

$v_K=\sqrt{2\gamma\frac{m_E}{r_E}}=11,2 \frac{km}{s}$