Grundlagen der Rotationsbewegung
Mathematische Grundlagen zur Kreisbewegung: Bogenmaß; Mathematische Grundlagen zur Kreisbewegung: Polarkoordinaten; Grundgrößen der Kreisbewegung; Kreisbewegung: Radialbeschleunigung und Zentripetalkraft; Sachaufgaben zu den Grundgrößen der Kreisbewegung
Beliebteste Videos und Lerntexte
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was ist eine Kreisbewegung?
Es ist egal, ob du in einem Karussell sitzt oder deinen Schreibtischstuhl rotieren lässt. Alle diese Bewegungen sind Kreisbewegungen. Diese Bewegungen lassen sich nicht einfach mit den Gesetzen, die du bisher für die geradlinige Bewegung kennengelernt hast, beschreiben. Jedoch lassen sich diese Gesetze dafür abwandeln (transformieren). Doch zunächst müssen wir dafür klären, was die Zeit , die Geschwindigkeit und Beschleunigung einer Kreisbewegung sind.
Größen der Kreisbewegung
Bei einer idealen Kreisbewegung, bewegt man sich exakt auf einer Kreisbahn. Die Zeit , die man dabei für eine vollständige Umrundung benötigt, nennt man Periodendauer .
Für die Anzahl der Umdrehungen in einer Sekunde, verwendet man die Frequenz . Diese ist der Kehrwert der Periodendauer .
und
Die Bahngeschwindigkeit unterscheidet sich je nach Entfernung vom Mittelpunkt. Stehst du also ganz außen auf einer Drehscheibe, bist du schneller unterwegs als eine Person, die näher an der Mitte steht. Die Winkelgeschwindigkeit , ist jedoch für alle Objekte gleich, da jeder Körper auf der Kreisbahn, egal wie weit er vom Mittelpunkt entfernt ist, in der gleichen Zeit den gleichen Winkel überschreitet.
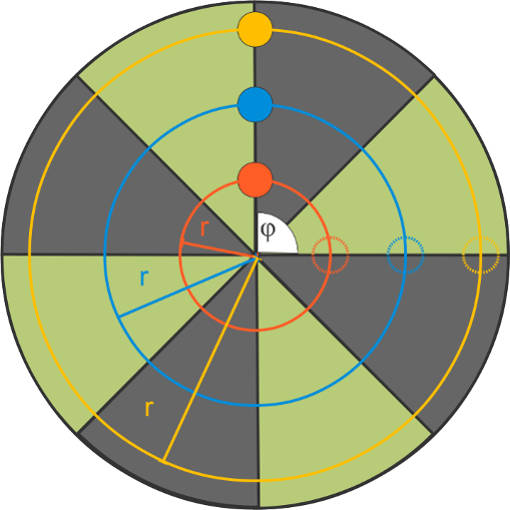
Winkel lassen sich auch im Bogenmaß angeben, dabei entspricht genau . Die Bahngeschwindigkeit entspricht dem Produkt der Winkelgeschwindigkeit und des Radius .
und
Die Radialbeschleunigung hält einen Körper auf seiner Kreisbahn. Die nötige Beschleunigung ist dabei von der Bahngeschwindigkeit und der Entfernung des Körpers vom Mittelpunkt abhängig. Sie lässt sich auch über die Winkelgeschwindigkeit berechnen.
Die Zentripetalkraft ist genau wie die Radialbeschleunigung zum Mittelpunkt der Kreisbewegung gerichtet. Sie ist nötig, um einen Körper mit der Masse auf der Kreisbahn zu halten und erzeugt die Radialbeschleunigung. Ihre Gegenkraft ist die Zentrifugalkraft, diese ist eine Scheinkraft.
Nutzung der Kreisbewegung
Schon eine der frühesten Jagdwaffen nutzte die Kräfte der Kreisbewegung aus, die Schleuder. Bei dieser wurde das Geschoss in einen Lederstreifen gelegt, dessen beide Enden zunächst in der Hand des Jägers verblieben. Dieser schleuderte die Schleuder nun sehr schnell über dem Kopf im Kreis. Im richtigen Moment ließ er eines der Enden los und das Geschoss flog nun geradlinig davon. Die Ägypter machten diese Waffe auch zu einer Kriegswaffe.
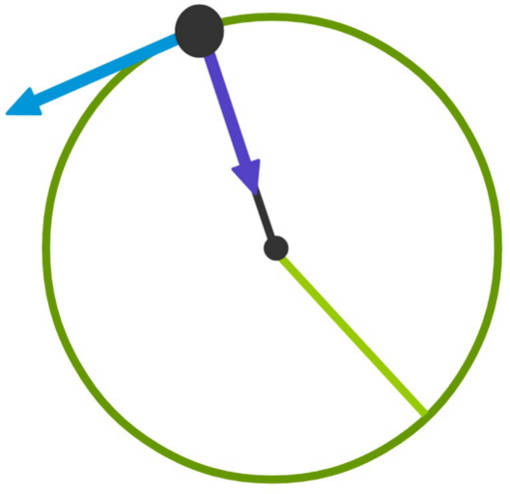
Auch beim Hammerwurf werden die Gesetze der Kreisbewegung genutzt. Kurz bevor das Gewicht von bis zu 7,26 kg losgelassen wird, besitzt es bereits die Energie, die ein tonnenschwerer Zug zum Anfahren benötigt.
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Grundlagen der Rotationsbewegung (3 Videos, 2 Lerntexte)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Grundlagen der Rotationsbewegung (4 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie
- Parallelschaltung
- Dopplereffekt, Akustischer Dopplereffekt











 Kreisbewegung – Umlaufdauer, Frequenz, Winkel- und Bahngeschwindigkeit
Kreisbewegung – Umlaufdauer, Frequenz, Winkel- und Bahngeschwindigkeit
 Radialbeschleunigung und Zentripetalkraft bei der Kreisbewegung
Radialbeschleunigung und Zentripetalkraft bei der Kreisbewegung
 Mit Bogenmaß und Polarkoordinaten eine Kreisbewegung berechnen
Mit Bogenmaß und Polarkoordinaten eine Kreisbewegung berechnen
 Polarkoordinaten bei der Kreisbewegung
Polarkoordinaten bei der Kreisbewegung









