Quantenphysik
Schrödingergleichung; Wasserstoffatom; Potenzialtopfmodell; Anwendungen des Potenzialtopfmodells; Tunneleffekt; Wasserstoffatom; Quantenzahlen und Orbitale; Quantenzahlen und Periodensystem; Laserstrahlung; Aufgaben zu Atommodellen der Quantenphysik
Beliebteste Videos
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Quantenphysik in der Schule und Wissenschaft
- Potentialtopfmodell
- Schrödingergleichung
- Quantenzahlen und Orbitalmodell
- Effekte und Anwendungen der Quantenphysik
Quantenphysik in der Schule und Wissenschaft
Namensgebend für die Quantenphysik sind Quanten. Dies sind gequantelte Energieportionen, also definierte Energiepakete. Die Quantenphysik wird in der Schule nur relativ kurz behandelt. Es geht hierbei hauptsächlich um das Kennenlernen der grundlegenden Modelle wie das Orbitalmodell und das Potentialtopfmodell. Die Quantenphysik beschäftigt sich wissenschaftlich mit der Energieübertragung von gequantelten Energiepaketen, und deren Bedeutung für die quantendynamischen Prozesse.
Potentialtopfmodell
Ein hilfreiches Modell zum Verständnis der Quantenphysik ist das Potentialtopfmodell. Der Potentialtopf ist ein von unendlich hohen energetischen Wänden begrenzter Raum, den die darin befindlichen Elektronen nicht verlassen können. Zudem können die Elektronen im Potentialtopf nur bestimmte Energiewerte aufweisen. Die Wellenfunktionen der Energiewerte werden als stehende Wellen im Potentialtopf dargestellt.
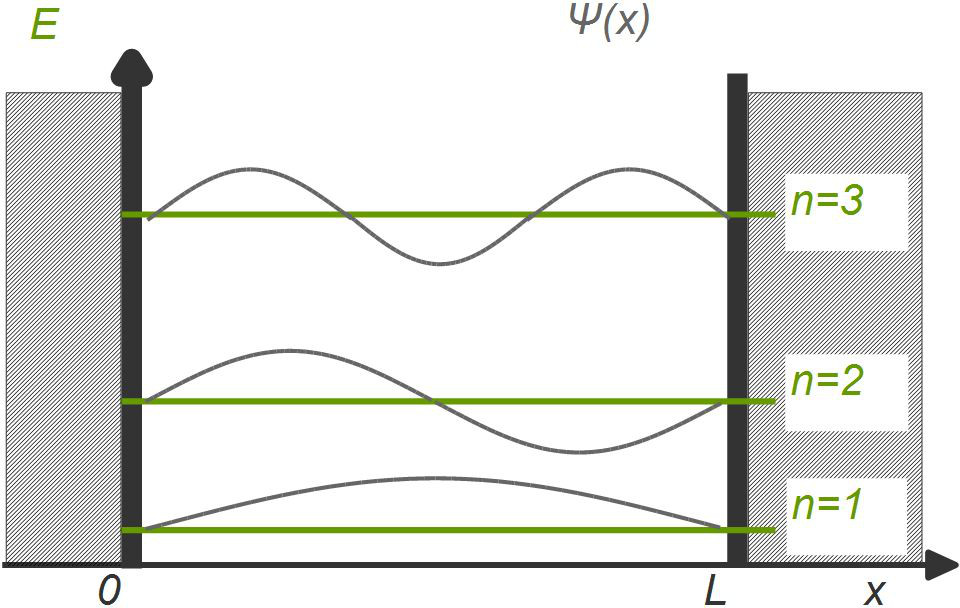
Die Wellenlängen dieser stehenden Wellen lassen sich über das Plank’sche Wirkungsquantum bestimmen.
$E= h \cdot f = h \cdot \frac{1}{\lambda}$
Durch die Einschränkung von Energiewerten werden auch die Lösungen der Schrödingergleichung begrenzt, da nur noch die Energiewerte der stehenden Wellen verwendet werden dürfen.
Schrödingergleichung
Mit der von Erwin Schrödinger entwickelten Gleichung lässt sich ein quantendynamisches System beschreiben. Nach der Schrödingergleichung wird jede Änderung des Systems über dessen Energie definiert. Die allgemeinste Form der Schrödingergleichung lautet:
$i\hbar\frac{\partial}{\partial t}|\psi(t)\rangle=\hat{H}|\Psi(t)\rangle$.
Die Energie ist in diesem Fall im Hamilton-Operator versteckt.
Die Schrödingergleichung lässt sich jedoch je nach Anwendungszweck erweitern. Zur Untersuchung der Ortsabhängigkeit eines quantendynamischen Systems wird die Gleichung zum Beispiel wie folgt erweitert:
$i\hbar\frac{\partial \psi}{\partial t}=-\frac{\hbar^2}{2m}\Delta\psi+V\psi$.
So wird die Gleichung zusammen mit dem Potentialtopfmodell auch für konkrete Aufgabenstellungen verwendet.
Wichtig zu wissen ist, dass die einfachen Lösungen der Schrödingergleichung keine Bedeutung besitzen, erst die quadratische Lösung der Schrödingergleichung gibt anschauliche Erkenntnisse. Die quadratische Lösung der Schrödingergleichung entspricht der räumlichen Aufenthaltswahrscheinlichkeit des untersuchten Elektrons bei den gewählten Parametern. Diese Erkenntnisse führen direkt zum Orbitalmodell und zu den Quantenzahlen mit denen sich die Elektronen in diesen Orbitalen beschreiben lassen.

Quantenzahlen und Orbitalmodell
Das Orbitalmodell beschreibt die Aufenthaltswahrscheinlichkeiten der Elektronen eines Atoms. Genau berechnet wurde es bisher erst für das einzelne Wasserstoffelektron. Größere Atome besitzen jedoch viel mehr Elektronen und durch die Gültigkeit des Pauli-Prinzips muss jedes Elektron in der Elektronenhülle eindeutig identifizierbar sein. Zur genauen Beschreibung der einzelnen Elektronen bedient man sich der vier Quantenzahlen im Atom:
Hauptquantenzahl:
$n=1,2,3,4,5,...$
Die Hauptquantenzahl beschreibt die Bohr’sche Schale in der sich das Elektron befindet. Der Zahlenwert 1 entspricht hierbei der K-Schale. Diese Zahl ist ebenfalls analog zum Energiezustand im Potentialtopf.
Nebenquantenzahl:
$0 \le l \le n-1$
Die Nebenquantenzahl oder auch Bahnquantenzahl definiert die Form des Orbitals. Sie kann Werte von 0 bis n - 1 annehmen und muss Element der natürlichen Zahlen sein.
Magnetquantenzahl:
$-l \le m \le +l$
Die Magnetquantenzahl bestimmt die räumliche Orientierung des Orbitals. Sie kann positive und negative natürliche Zahlen annehmen und bewegt sich zwischen - l bis + I.
Spinquantenzahl:
$s=+\frac{1}{2}\text{ oder }s=-\frac{1}{2}$
Die Spinquantenzahl definiert die Richtung der Eigenrotation der Elektronen. Dies ist das abschließende Unterscheidungsmerkmal zweier Elektronen, da es in jedem Orbital eine Doppelbelegung geben kann. Man spricht von Spin-Up und Spin-Down. Da die Elektronen immer rotieren müssen, kann die Spinquantenzahl nur + ½ oder - ½ sein.

Effekte und Anwendungen der Quantenphysik
Neben den Grundlagen der Quantenphysik werden mit diesen Modellen auch einzelne Effekte akkurat beschrieben, z.B. der Tunneleffekt. Bei diesem Effekt gelingt es Elektronen, aus dem Potentialtopf auszubrechen, ohne die Potentialbarrieren überwinden zu müssen. Zudem lässt sich über die Quantenphysik die Funktionsweise eines Lasers erklären.
Alle Videos zum Thema
Videos zum Thema
Quantenphysik (6 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Quantenphysik (5 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie
- Parallelschaltung
- Dopplereffekt, Akustischer Dopplereffekt












 Schrödingergleichung und Potentialtopfmodell
Schrödingergleichung und Potentialtopfmodell
 Schrödingergleichung und Potentialtopfmodell (Übungsvideo)
Schrödingergleichung und Potentialtopfmodell (Übungsvideo)
 Quantenzahlen im Atom
Quantenzahlen im Atom
 Tunneleffekt
Tunneleffekt
 Laser
Laser









