Differenzialgleichungen und komplexe Anwendungen von Arbeit, Energie und Leistung
Mechanische Arbeit als Prozessgröße und mechanische Energie als Zustandsgröße; Die kinetische Energie; Arten der Arbeit; Energieumwandlungen; Mechanische Leistung; Energie, Kraft, Arbeit, Leistung, Potential und Feld
Beliebteste Videos
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Was sind Differenzialgleichungen?
Differenzialgleichungen haben, wie du im Namen erkennen kannst, tatsächlich etwas mit differenzieren (ableiten) zu tun. Denn es kommen Ableitungen einer Funktion vor. Wird die Gleichung gelöst, wird kein konkreter Wert, sondern eine oder mehre gleichartige Funktionen gefunden.
Das klingt auf den ersten Blick sehr kompliziert, doch hier wird dir ein Licht aufgehen: Stell dir vor, du suchst nach einer Funktion $f$, deren Ableitung mit der Funktion komplett übereinstimmt. Mathematisch kannst du das so formulieren:
$ f(x) = f^\prime (x) $
Vielleicht die Sinusfunktion? Leider nein, denn die erste Ableitung ist ja die Kosinusfunktion. Aber du kommst bestimmt selbst auf das richtige Ergebnis…
Doch was haben Differenzialgleichungen in der Physik verloren? Warum werden diese benötigt? Tatsächlich bilden diese die Grundlage der Newton’schen Mechanik!
Differenzialgleichungen in der Mechanik
Viele Formeln, die du bisher in der Mechanik gelernt hast, wurden von Newtons Axiomen über sogenannte Bewegungsgleichungen abgeleitet. Fast jedes mechanische Problem führt auf eine Differenzialgleichung. Du bist bisher vielleicht noch nicht damit in Berührung gekommen, weil du die „fertigen“ Formeln bekommen hast.
Wie du bestimmt weißt, spielen in der Mechanik Bewegungsvorgänge eine wichtige Rolle. Daher hängen viele Formeln von der Zeit ab. Ableitungen nach der Variable $t$, also nach der Zeit, haben daher eine Kurzschreibweise erhalten:
$ s^\prime (t) = \frac{ds}{dt} = \dot{s}(t) = \dot s\\ s^{\prime\prime} (t) = \dfrac{ds^2}{dt^2} = \ddot{s}(t) = \ddot s $
Vielleicht kannst du dich noch erinnern, dass der Weg $s(t)$, die Momentangeschwindigkeit $v(t)$ und die Momentanbeschleunigung $a(t)$ einen engen Zusammenhang haben:
$ v(t) = \frac{ds}{dt} = \dot s\\ a(t) = \frac{dv}{dt} = \dot v = \ddot s $
In den nachfolgenden Beispielen werden dir solche Ableitungen in Differenzialgleichungen begegnen:
Beispiel: Freier Fall
Eine Punktmasse mit $m = 8,0kg$ fällt aus einer Höhe $h_{max} = 5,0m$ auf den Boden. Die Reibung wird vernachlässigt.
Mit welcher Endgeschwindigkeit $v_E$ prallt die Masse auf den Boden? Welche Beschleunigungsarbeit wird dabei verrichtet und welche (Momentan-)Leistung kurz vorm Aufprall erbracht?
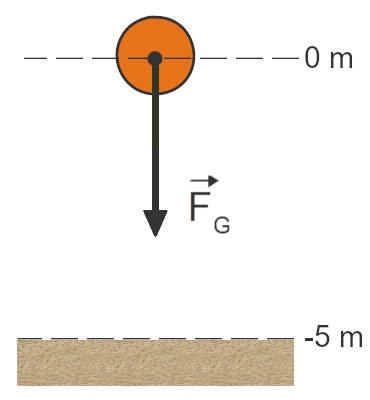
Ohne Differenzialgleichungen rechnen
Die erste Frage kannst du recht einfach mit dem Energieerhaltungssatz beantworten, indem du die potentielle Energie mit der Bewegungsenergie gleichsetzt:
$ E_{pot}=E_{kin}\\ m\cdot g \cdot h_{max} = \frac{1}{2}m v_{E}^2\\ g\cdot h_{max} = \frac{1}{2} v_{E}^2\\ \sqrt{2\cdot g \cdot h_{max}}= v_{E}\\ \sqrt{2\cdot 9,81\frac{m}{s^2} \cdot 5m}= 9,9\frac{m}{s}\\ $
Für die Beschleunigungsarbeit, welche bis zum Aufprall verrichtet wird, kannst du folgendes berechnen:
$ W_{kin} = \Delta E_{kin} = \frac{1}{2}m v_{E}^2 = \frac{1}{2}8 kg \cdot (9,9 \frac{m}{s})^2 = 392 J\\ $
Um die mechanische Leistung zu berechnen, benötigst du noch die Zeit, in der die Arbeit verrichtet wird, also die Fallzeit. Dafür kennst du vielleicht noch die Formel $t = \sqrt{\frac{2h}{g}}$ und erhältst für die Zeit bis zum Aufprall etwa $t = 1,0s$.
Die mittlere Beschleunigungsleistung $P$ ist dann der Quotient aus Arbeit und Zeit. Damit ergibt sich ein Wert von $P= 392 W$.
Die Rechnungen waren recht einfach, weil du mit den gewohnten Formeln rechnen konntest. Aber woher kommen eigentlich die Formel für die kinetische Energie und die ganzen anderen Formeln eigentlich?
Mit Differenzialgleichungen rechnen
Die Aufgaben sollen nun „ohne“ Formeln gelöst werden. Als Grundbedingung wird das zweite Newton’sche Axiom $F= m\cdot a$ vorausgesetzt. Die einzige Kraft, die beim freien Fall ohne Reibung wirkt, ist die Gewichtskraft. Damit kann zunächst die Bewegungsgleichung als Differenzialgleichung aufgestellt werden:
$ m\cdot a(t) = m\cdot \ddot s = -m\cdot g\\ \ddot s = - g $
Das bedeutet, die zweite Ableitung des Weges nach der Zeit ist gleich der negativen Erdbeschleunigung. Um nun die Gleichung des Weges $s(t)$ zu erhalten, muss zweimal hintereinander integriert werden:
$ \ddot s = - g\\ \int (\ddot s) dt = \int( – g) dt\\ \dot s + v_0 = -gt\\ \int (\dot s + v_0) dt = \int (-gt) dt\\ s(t) + v_0\cdot t + s_0 = - \frac{g}{2} t^2\\ s(t) = - (\frac{g}{2} t^2 + v_0\cdot t + s_0) $
Die Integrationskonstanten $v_0$ und $s_0$ der Stammfunktion sind physikalisch als Anfangsgeschwindigkeit und -weg zu interpretieren. Im Beispiel sind beide null, da der Nullpunkt und die Ausrichtung des Koordinatensystems geschickt gewählt wurde. Da die Geschwindigkeit die erste Ableitung des Weges nach der Zeit ist, ergibt sich dadurch auch:
$ v(t) = \dot s(t) = - g \cdot t $
Um nun die Aufprallgeschwindigkeit $v_E$ berechnen zu können, wird die Zeit $t_E$ bis zum Aufschlag benötigt. Sie ergibt sich durch Einsetzen in die Bewegungsgleichung:
$ -5m = - \frac{g}{2} t_{E}^2\\ t_E = 1,0 s $
Durch das Einsetzen dieser Zeit in $v(t)$ wird schließlich die Aufprallgeschwindigkeit $v_E$ zu etwa $9,8 \frac{m}{s}$ ermittelt.
Die gesamte Beschleunigungsarbeit, welche zu den mechanischen Arbeitsformen zählt, kann nun über ihre Definition $W(t_E) = F\cdot s(t_E)$ berechnet werden:
$ W(t_E) = - m\cdot g \cdot (- \frac{g}{2} t_{E}^2) = \frac{m}{2}\cdot (g\cdot t_E)^2 = \frac{m}{2} \cdot v_{E}^2 = \frac{8kg}{2}\cdot (9,8\frac{m}{s})^2 = 395 J $
Die mittlere Leistung $P$ kann ebenfalls über ihre Definition berechnet werden:
$ P=\frac{\Delta W}{\Delta t} = \frac{395J}{1s}= 395 W $
Die Momentanleistung unmittelbar vor dem Aufprall kann hier ebenfalls berechnet werden. Dafür wird ein unendlich kleiner Zeitabschnitt $dt$ für $\Delta t$ gewählt:
$ P(t)=\frac{dW}{dt}=\dot W(t)\\ \Rightarrow P(t_E)= \dot W(t_E) = mg^2\cdot t_E = 8kg\cdot g^2 \cdot t_E = 770 W $
Alle Videos zum Thema
Videos zum Thema
Differenzialgleichungen und komplexe Anwendungen von Arbeit, Energie und Leistung (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Differenzialgleichungen und komplexe Anwendungen von Arbeit, Energie und Leistung (2 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie
- Parallelschaltung
- Dopplereffekt, Akustischer Dopplereffekt






 Energieerhaltungssatz am Beispiel des Fadenpendels
Energieerhaltungssatz am Beispiel des Fadenpendels
 Begriffe der Mechanik (Überblicksvideo)
Begriffe der Mechanik (Überblicksvideo)









